無題
無題
ボッシュ さんの書込 (2005/02/08(Tue) 00:38)
こんにちわ〜初めましてボッシュと申します.大学入試で悩んでいる高校三年生です.まことにこんなレベルの高い掲示板に書くことではないことだと思うんですが,どうしても矛盾していて納得いかない現象があります.それは,コンデンサーの静電エネルギーと電池のする仕事との関係です!あれはどう見てもエネルギー保存則に反しているじゃないですか!
Re: 無題
Joh さんのレス (2005/02/08(Tue) 00:41)
具体的に,どの点がエネルギー保存則に反していると思うのか詳しく教えてください.
Re: 無題
おこめ さんのレス (2005/02/08(Tue) 00:58)
電池のところでは回路にエネルギーを供給するので非保存的な場になっているんですよ.起電力という言葉は聞いた事はありますか?そこがポイントです.
もうちょっとヒント
回路のあらゆる場所でオームの法則が成り立つという仮定を置かれていると思います.しかし,これが誤りなのです.
なんかやっぱり具体的にどこが矛盾しているように考えているのかはっきりしないとどうにも言いようが無いですね :(
Re: 無題
崎間 さんのレス (2005/02/08(Tue) 01:25)
ボッシュさんはじめまして.Johさん,おこめさんも書かれているように,ボッシュさんがどういうふうに矛盾してると考えているか分からないと,どうしようもないのですが
> あれはどう見てもエネルギー保存則に反しているじゃないですか!
これは聞き捨てならないので (--;.ボッシュさんの周りでも,矛盾だと考えておられるのでしょうかー? どのあたりでそう悩んでおられるのか,気になりますね.
Re: 無題
tomo さんのレス (2005/02/08(Tue) 02:16)
ボッシュさん,初めまして. ボッシュさんが感じてらっしゃる矛盾とは,以下のようなものでしょうか?
起電力Vの電池と,電気容量Cのコンデンサーをつないだ回路において, コンデンサーに電荷Qがたまるまでに電池がした仕事は,QV. この時コンデンサーにたまっている静電エネルギーはQV/2. この2つが一致しないとおかしい!矛盾してる!
違ったら読み飛ばしてください (--;.
Re: 無題
崎間 さんのレス (2005/02/08(Tue) 10:26)
> コンデンサーに電荷Qがたまるまでに電池がした仕事は,QV. > この時コンデンサーにたまっている静電エネルギーはQV/2. > この2つが一致しないとおかしい!矛盾してる!
なるほど.いやしかし,教えられたことを鵜呑みにせず,疑ってかかるボッシュさんの姿勢はすばらしいですね.僕も見習いたいものです.
# 電荷量 x 電圧で仕事(エネルギー)を求めている部分がトリックですね.
ようこそ,高校生!
やかん さんのレス (2005/02/08(Tue) 12:09)
ボッシュさん,はじめまして!ようこそいらっしゃいました! いよいよ,受験本番ですね.緊張するなと言っても 難しいと思いますが,インフルエンザが流行ったりしてるので,体調には くれぐれもご注意下さい.
>あれはどう見てもエネルギー保存則に反しているじゃないですか!
アハハ,過激ですね!(^^;)もちろんそんな事はないと思いますが, これだけ強い矛盾,疑問をお持ちなら,きっと問題が解決した時に より深い理解が定着すると思いますよ.せっかくこれだけレスがついた事だし, この機会に私も一緒に勉強しなおそうと思うので,よろしかったら詳しくお考え教えてくださいね.
皆さんありがとうございます!
ボッシュ さんのレス (2005/02/08(Tue) 21:50)
> コンデンサーに電荷Qがたまるまでに電池がした仕事は,QV. > この時コンデンサーにたまっている静電エネルギーはQV/2. > この2つが一致しないとおかしい!矛盾してる!そうそう!そこなんですよ!私にはどうしても理解できません・・・残りのQV/2はどこに行ってしまったのか・・実はあと三日でテストなんで早いとこお願いします^^;あっでも物理科志望だからこれからもつき合うか・・・・ついでに言いますとエネルギーって何ですか?
Re: 皆さんありがとうございます!
崎間 さんのレス (2005/02/08(Tue) 22:07)
> そうそう!そこなんですよ!私にはどうしても理解できません・・・ > 残りのQV/2はどこに行ってしまったのか・・
コンデンサの両端の電位  は,時間に応じて変化しています.
は,時間に応じて変化しています.  が一定ならば,エネルギー(
が一定ならば,エネルギー(  とします)は
とします)は 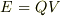 で表せます.
で表せます.
が,  は一定ではなく時間変化しますので,実際には
は一定ではなく時間変化しますので,実際には
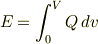
として求める必要があります.ここで  は電圧の変数です.この積分を実行すると
は電圧の変数です.この積分を実行すると 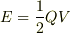 が得られます.ですから,そもそも
が得られます.ですから,そもそも
> 残りのQV/2
など「はじめからない」のです.したがってエネルギー保存則も成立しています.
> エネルギーって何ですか?
(--; これはまた難題です.僕などには即答できません….
Re: 皆さんありがとうございます!
CO さんのレス (2005/02/08(Tue) 23:06)
あれ,電池のした仕事は 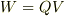 で表されるんですよね?
で,コンデンサに溜まっている静電エネルギーが
で表されるんですよね?
で,コンデンサに溜まっている静電エネルギーが 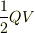 ならば,やはり
ならば,やはり 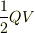 がどこかに消えていると思います.
がどこかに消えていると思います.
ジュール・・
Re: 皆さんありがとうございます!
崎間 さんのレス (2005/02/08(Tue) 23:19)
うわっ,変なこと書いてしまいました.No.4153の
> ですから,そもそも >> 残りのQV/2 > など「はじめからない」のです.したがってエネルギー保存則も成立しています.
の部分は無視してください.すいません.
Re: 皆さんありがとうございます!
おこめ さんのレス (2005/02/08(Tue) 23:27)
この場合の全エネルギー保存の法則は力学的エネルギーと電磁エネルギーの和が保存されているということですね.たしか高校でも習った覚えがあります(だから入試に出るかもしれないということですか・・・).
Re: 皆さんありがとうございます!
tomo さんのレス (2005/02/08(Tue) 23:32)
ボッシュさん,みなさんこんばんは. tomo@就活中M1です.
> そうそう!そこなんですよ!私にはどうしても理解できません・・・残りのQV/2はどこに行ってしまったのか・・
どんぴしゃでしたね.私も散々ここで悩みましたから・・・ (--; . どこへ行ってしまったのでしょうか.レスポンスを読んでみましょう.
Re: 皆さんありがとうございます!
ファインメン さんのレス (2005/02/09(Wed) 01:10)
はじめまして,みなさん. 以前から,ここのHPは拝見させてもらってたんですが,書き込むのは初めてです. どうぞ,よろしくお願いしますm(__)m
ところで,消えたエネルギーについてですが,ジュール熱で間違いないと思いますよ. なぜかよいうと,大学入試問題ではよくコンデンサーのみ組み込まれている回路がありますが,あれは問題を複雑にしないためにそうしているだけです. もし仮に,理想的にコンデンサーのみで組まれる回路があったとしたらどうなっちゃうでしょう?? コンデンサーに電圧をかけた瞬間に全電荷がたまってしまい,コンデンサーは壊れますよね. (大学生になると回路の微分方程式を解きますが,抵抗がないと時定数すらきまりませんよね.) なんで,あれは抵抗でのジュール熱だと思いますよ(^^) (ちなみの僕も浪人時代にその疑問を持ちました(笑))
Re: 皆さんありがとうございます!
ken さんのレス (2005/02/09(Wed) 10:09)
>そうそう!そこなんですよ!私にはどうしても理解できません・・・残りのQV/2はどこに行ってしまったのか
kenです.こんにちは.
別の方向から考えて見ましょう.
電池の電圧をEとします. 最初は放電しきった状態のコンデンサーC を電池にいきなりつなげるとします. コンデンサーCの電荷をQ(電池につなげる直前はQ=0) コンデンサーCの両端間電圧をVとします. <pre> ここを時刻t=0でつなげる --------------●---/ ------------- |点A |コンデンサーC ----- ----- --- 電池E ----- | | | ------GND / / / </pre> さて,時刻t=0で電池EとコンデンサーCを接続したとする. この直後における点AのGNDに対する電位を考えて見ます. 電池Eが接続されていることを考えると点Aの電位はEになります. 同時に,コンデンサーCの方をみると,まだ電荷がたまっていないので V=0となります. とすると, 電池EとコンデンサーCを接続する配線に抵抗がなく, 電池EとコンデンサーC内部にも抵抗成分がまったくない理想的な 状態を仮定すると 点Aの電位は,Eであり,同時にV(=0)であるということになります. 下の図もどき,において,横軸はコンデンサにたまっている電荷Q 縦軸を電位にとると,電池の電圧は常にE コンデンサ電圧VはQに対して直線的にのびていくものになります. 電池がした仕事は囲まれた長方形の全て(=EQ) コンデンサに蓄積された仕事は右下の三角のエリアとなります.
<pre> 点Aの電位 | E |------------ | /| | / | | / | | /V | | / | | / | |/ | 0 +------------------コンデンサの電荷 Q </pre> 左上の三角形の部分はどこに消えたのだろう. さらにEとVの電位差はどこに発生しているのだろう.
Re: 皆さんありがとうございます!
やかん さんのレス (2005/02/09(Wed) 16:04)
私自分で理解してないのでなんなのですが, 参考になりそうなURLがありました. http://www7.plala.or.jp/stokida/l2h/katogene/node4.html
Re: 皆さんありがとうございます!
おこめ さんのレス (2005/02/09(Wed) 20:36)
kenさんの考えるような状態は現実として作り出すことは近似的にも難しいように思います.そもそも電位差を抵抗なしに作り出すということが可能なのですか?電源の内部抵抗をゼロと置いたら自動的に電位差もゼロになりそうです.そうだとしたら上の仮定自体破綻してしまいそうです. 内部抵抗がある場合,やかんさんの見つけたページのような結果になるのでしょうね.
以上の発言が妥当かどうかを調べるには内部抵抗をrとしてRC回路を解き,r→0の極限を考えれば良いでしょう.発散すれば実現不可能.意味のある値が得られれば何か分かると思います.
今,やかんさんが張ったページで確認しましたが,この考え方だと電流が発散して物理的に意味を持たなくなるみたいです(ホントかな?).
仮にこの状況が現実世界でどのようになっているのかを考えるならば,小さな抵抗のもとで高電圧を掛けた場合に相当すると思います.コンデンサーが壊れない(この仮定も苦しいです.しかも放電しないと仮定する必要もあると思います.この時点で完全な空想の話です)と考えた場合,無限の強さの電流が無限小時間流れる.このときに発生するジュール熱が積分することによってQV/2の大きさになる(電流と時間のグラフがディラックのδ関数の形になるということになります).こういうことになりそうです.このように無限大に意味を持たせれば,エネルギー保存則は守られそうです.
こんな風に用意された道具の中で考えていくのも面白いですね.高校の公式がいつも成り立つんだと考えてみると,どこが適用範囲を超えているのかとか色々と考えをめぐらすことができそうです.ホントいつもはこんな風に考えて,うまくいかなかったときに何が足りないのか調べる,考えるなどするのが勉強なのかもしれません.
ホントは次に現実に起こる現象を考える必要があると思いますが,それでは元の話から大幅にそれてしまいます.この書き込み自体,迷惑なものでしかないかもしれませんが,許してください.
Re: 皆さんありがとうございます!
ぼっしゅ さんのレス (2005/02/10(Thu) 00:02)
> この書き込み自体,迷惑なものでしかないかもしれませんが,許してください.いえいえそんな^^貴重な意見ありがとうございました.実はわたくしエネルギー保存自体よくわからないんですよ.ある参考書によると「ある系ではすべてのエネルギーの和は保存する」って書いてあるんですよ,でも実際問題をやってみると,仕事とかって考える立場によって正負が変わるじゃないですか,そこら辺どうして言いかよくわからなくて・・・エネルギーってすべて正として考えて足し合わせるだけでいいんでしょうか?それとも正負をきっちり考えて式をたてなければならないんでしょうか?正負を考えるとき何を基準にすればいいんでしょうか?
Re: 皆さんありがとうございます!
おこめ さんのレス (2005/02/10(Thu) 00:11)
正と負を考えなければなりません.確かではありませんが回路の基準点は接地点だと思います.
エネルギー保存則についてですが,これは電磁気学を勉強すればいずれ分かります.回路と電気を半ば別々に扱う高校物理の範囲でこころから理解するのは難しいのかもしれません.
Re: 皆さんありがとうございます!
tomo さんのレス (2005/02/10(Thu) 00:50)
ぼっしゅさん,みなさん,こんばんは. tomo@就活中M1です.
> 仕事とかって考える立場によって正負が変わるじゃないですか,そこら辺どうして言いかよくわからなくて・・・エネルギーってすべて正として考えて足し合わせるだけでいいんでしょうか?それとも正負をきっちり考えて式をたてなければならないんでしょうか?正負を考えるとき何を基準にすればいいんでしょうか?
う〜ん…どこかで仕事とエネルギーがごっちゃになってしまっているのでしょうかね. 仕事とエネルギーは別物ですので,その辺りについてもう一度見直してみてはいかがでしょうか.
Re: 皆さんありがとうございます!
やかん さんのレス (2005/02/10(Thu) 01:22)
>ついでに言いますとエネルギーって何ですか? うわっ,難しいですね.ちゃんとした事私が答えられるわけ ありませんが,高校レベルの解答,理解でよいのなら 確か教科書には”仕事をする能力”って,書いてあったような気がします. エネルギーが形を変えて,熱になったり,音になったり,自動車走ったり, 電車走ったりするんでしょうね.物理的な定義はきちっとあっても,形も 大きさも色もない,”日常の感覚”からすると抽象的とも思える概念ですかね. こりゃあ,そういうもんだと割り切って定義覚えるしかないのかな.でもよく日常 ”エネルギー”って,言葉使ってますよね.”仕事をやる気力”みたいな感じで. 非科学的な言い方だし,人に言ったら笑われたり怒られたりするだろうけど, こっそり,自分だけでそういう風に思っていたら,親しみ沸くかもしれませんね. そういえば,ニュートン力学に出てくる”力”も,日常感覚にぴったりだけど, よく考えると色も形も大きさもないし,何で発生するかも説明されてないですよね. でも殴られて痛いのは,力を受けたせいだって,納得して言葉使ってるし,ようするに 慣れれば違和感ないのかな.
Re: 皆さんありがとうございます!
おこめ さんのレス (2005/02/10(Thu) 02:03)
日常生活で使われているエネルギーは人にとって利用可能なエネルギーのみをエネルギーと言います.力の場合はどうなんでしょうか?
そういえばエネルギー,仕事って高校の教科書に詳しく載ってましたっけ? 仕事は運動エネルギーの変化に等しいです.さらに保存力(保存場)ならばポテンシャルエネルギーの変化(符号は逆)にも等しくなります.
Re: 皆さんありがとうございます!
やかん さんのレス (2005/02/10(Thu) 03:06)
あっ,保存場って,出発点と終点が決まれば経路によらず,する仕事が同じになる,だったかな.gradでスカラーfが存在するのが・・,あれえ??きちんと覚えてないからだめですね (^^;
Re: 皆さんありがとうございます!
Mathmatica3000 さんのレス (2005/02/10(Thu) 10:50)
横やりですみませんが,何で電池のする仕事が「QV/2」になるんですか? なりますかね?
Re: 皆さんありがとうございます!
おこめ さんのレス (2005/02/10(Thu) 14:42)
どうもはじめまして,Mathmatica3000さん.ところで電池のする仕事がQV/2となるという趣旨の発言はどこにあるのですか?後,何でではなく,違うと思ったら具体的な計算など(方法でも十分です)を示してもらうと助かります.
Re: 皆さんありがとうございます!
Mathmtica3000 さんのレス (2005/02/10(Thu) 18:00)
返信ありがとうございました. 間違えました,電池がする仕事は「QV」になるのは何故ですか,でした. この議論は上の方にCOさんが書き込みをされています. 私は,電池の起電力と電位差とを勘違いしていませんか?ということを言いたいのです.
具体的な計算はあります. この場合は静電的なので,片方の極板から電荷をちょこっとずつ準静的に運ぶのです.
Re: 皆さんありがとうございます!
ken さんのレス (2005/02/10(Thu) 18:55)
kenです.こんばんわ.
>私は,電池の起電力と電位差とを勘違いしていませんか?ということを言いたいのです.
Mathmtica3000の言おうとしていることは,
「起電力とはあるなんらかの条件のもとで可能な電圧値」であって, 起電力1.5Vの電池が,低い抵抗値の場合にまで電位差1.5Vをだせるわけではない. (例えば,0.1Ωでつながれたときに15A-1.5V出力はありえず,電池の出力の 電位差は起電力1.5Vよりずっと低い値になる) コンデンサーをつないだ場合(ほぼショートと同等の状態)まで起電力V が出るわけではないから電池がする仕事は「QV」ではない.
という意味でしょうか?
>具体的な計算はあります. >この場合は静電的なので
についてですが,どのような計算でしょうか. 「静電的」といわれると電流や電荷,電位,電界がゆっくりとしか 変化しないようなイメージを持ってしまっていますが, ここで言っている「静電的」とはどのような意味でしょうか.
Re: 皆さんありがとうございます!
Mathmatica3000 さんのレス (2005/02/10(Thu) 19:42)
初めからコンデンサの電位差がVだとは考えられません. 電池を使ったら,コンデンサを充電する仮定で,過渡的な仮定を経なければいけません. 何故,このような複雑な状況下で,「QV」と計算できるのでしょうか? 計算の仮定を教えてください.
静電場を乱さないように,電磁波の放射がないように,準静的に電荷を移動させる,という意味です.
Re: 皆さんありがとうございます!
Mathmatica3000 さんのレス (2005/02/10(Thu) 19:43)
しつれいしました 「仮定」→「過程」 です.すみません.
Re: 皆さんありがとうございます!
CO さんのレス (2005/02/10(Thu) 20:28)
> 初めからコンデンサの電位差がVだとは考えられません. > 電池を使ったら,コンデンサを充電する仮定で,過渡的な仮定を経なければいけません.
 という文字が複数の意味で使われていて混乱が生じている気がします.
私の書き込みは,過渡的な現象は終わったあとの話です.つまり,コンデンサの電位差
という文字が複数の意味で使われていて混乱が生じている気がします.
私の書き込みは,過渡的な現象は終わったあとの話です.つまり,コンデンサの電位差  は電源電圧
は電源電圧  に等しく,両方とも const. です.
に等しく,両方とも const. です.
> 何故,このような複雑な状況下で,「QV」と計算できるのでしょうか? > 計算の仮定を教えてください.
計算の過程が知りたいですか?
簡単に書けば,電池が電位差 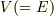 を
を  の電荷だけ汲み上げたのですから,電池のした仕事は
の電荷だけ汲み上げたのですから,電池のした仕事は 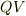 となるはずではないですか?
となるはずではないですか?
Re: 皆さんありがとうございます!
Mathmatica3000 さんのレス (2005/02/10(Thu) 23:10)
COさん, >簡単に書けば,電池が電位差をの電荷だけ汲み上げたのですから,電池のした仕事はとなるはずではないですか? 電位差Vがコンデンサ内で成立している段階で,また電荷を運んでしまっては,さらに電位差が増えるだけです. 電位差Vがコンデンサ内で成立している段階では,既にコンデンサ内には「QV/2」というエネルギーは貯められています.
おこめさん, >この場合は静電的,ちょっとずつとか曖昧な表現だと思います. このコンデンサに貯められている「QV/2」というエネルギーは,「静電的」という特別な場合にのみ成り立ちます. 「静電的」というのは電荷の移動により,電磁波が発生することを防ぐ,ということです. 何故防がなければならないのか,それは,電磁波によりエネルギーが逃げてしまうのを防ぐためです.
Re: 皆さんありがとうございます!
Mathmatica3000 さんのレス (2005/02/10(Thu) 23:10)
お二人への私の解答の正当性を,具体的な計算過程を踏まえて示しましょう.
?初めコンデンサは充電されていない.現在の電位差Vは,極板Bから正電荷を少しずつ取り出して極板Aに運び込むことによって形成する. ?極板Bから微小電荷dqを運ぶ.この際其の微小電荷dqに,
![dw = dq[\phi(A)-\phi(B)]](http://hooktail.maxwell.jp/bbslog/e2f3c47e56ad30103182e441123c35fb.png)
だけの仕事をする必要がある.
ここで 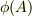 と
と 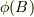 は,両極板上に+q,-qの電荷がそれ
ぞれ分布しているときの,それぞれの極板の電位である.
?コンデンサーの静電容量
は,両極板上に+q,-qの電荷がそれ
ぞれ分布しているときの,それぞれの極板の電位である.
?コンデンサーの静電容量
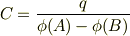
は極板上の電荷の量に依らない定数である.これを使えば
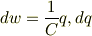
?積分を実行する.移動する電荷の合計量は+Qとする.
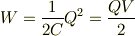
よって,電位差Vが成立している段階で,電荷は+Qだけ移動しており,そのときエネルギー「QV/2」が貯められている.
Re: 皆さんありがとうございます!
おこめ さんのレス (2005/02/10(Thu) 23:25)
すいません,以前の書き込み消してしまいました. 上の説明ですが,これはコンデンサーがなされる仕事ですね.電池のする仕事ではないと思いますよ.
>このコンデンサに貯められている「QV/2」というエネルギーは,「静電的」とい>う特別な場合にのみ成り立ちます. >「静電的」というのは電荷の移動により,電磁波が発生することを防ぐ,という>ことです. >何故防がなければならないのか,それは,電磁波によりエネルギーが逃げてしま>うのを防ぐためです.
うーん,静電的という意味の一部というか結果そういうことが言えるという事ですが,これがイコール静電的ということではないです.極めて幅の広い意味を持つ静電的という言葉をどういう意味使っているのか示してもらうことは話をする上で必要なことだと思います.後,時間変動する場イコール電磁波発生という風にもとれますが,そのようなことはないと思います.どうも解説ありがとうございました.
Re: 皆さんありがとうございます!
Mathmatica3000 さんのレス (2005/02/10(Thu) 23:38)
電池=我々が電荷を移動させるのに必要な手段 それによって仕事を電荷にする. コンデンサに真空のゆがみが出来る. それが,コンデンサにためられたエネルギー.
おこめさん,私は貴方に対し,曖昧に答えたつもりはありません. なぜならば,物理専攻の人間が当然知っておくべき内容だと,この議題を認識しているからです. もちろん受験中の高校生の方は,ご存じないでしょうが.
静電場は電磁波の放射を防ぐため,と私は書き込みをしました. 電磁誘導からわかるように,電磁場は電荷・電流という起源なしに発生しますね. そして電磁場が時間変化すると,電磁波が放射されます. 電磁波は運動量を持ち,エネルギーを運び,エネルギー保存を説明するために必要な,物理的実在です. この電磁場というものを認識出来てこそ,当初エーテルのゆがみと考えられた,ファラデー・マクスウェルの近接作用理論が理解出来た,と言う事になるのです.
あなたは「静電磁場でほぼ完成」というようなことを,口にした事がありませんか?
コンデンサを充電する過程は,準静的(静電的)として,私は示しました. 静電場は準静的,これはどういう意味でしょうか? 力学で「重力の中で,質点を持ち上げ,ポテンシャルエネルギーの増加を計算」したのと何ら変わりはないのです. これでは,遠隔作用論で十分です. 「静電的」なコンデンサの充電は,教育上の課程として,取り上げられているだけなのです.
以上が,私の主張です.
Re: 皆さんありがとうございます!
おこめ さんのレス (2005/02/11(Fri) 00:04)
>静電場は電磁波の放射を防ぐため,と私は書き込みをしました. これは極めて人為的な言葉の使い方(電磁波の放射を防ぐためでなく,そのような場合というのが自然だと思います)ですが,意味は十分分かると思います.すみませんでした.
>電磁誘導からわかるように,電磁場は電荷・電流という起源なしに発生しますね.
これは違いますよ.起源はいつも電荷・電流だと思います.原因なしに場がなぜできるのですか?外場としてある場も実際には系の外に電荷が存在しているのです.これは電磁相互作用を遠隔作用と考えるより深刻な問題です.
>時間変動する場イコール電磁波発生という風にもとれますが,そのようなことはないと思います.
これは任意の場所において電磁波が発生することではないという事が言いたかっただけです.不正確でした.よく分かりませんが,電磁波の発生はローレンツ条件に従う必要があります.他にも境界条件もかかわると思います.はっきりと理解しているわけではないのでどなたか教えていただけませんか?
>あなたは「静電磁場でほぼ完成」というようなことを,口にした事がありませんか? 確かに以前その段階で数学的な道具がそろってしまうという発言はした覚えがあります.物理的な話ではないです.
あまり怒らないでください.物理専攻なら常識だとかそういう話をされるとつまらないし,発言しにくくなるでしょう.間違っているなと思ったらその人に分かるように説明してください.ここはそういう場だと思います.
それから後,コンデンサーがなされる仕事が電池のする仕事に等しいことを示さなければこの問題に答えたことにはなりません.
>「静電的」なコンデンサの充電は,教育上の課程として,取り上げられているだけなのです.
これが答えということですか?最終的に落ち着いたときにコンデンサーに溜まるのは静電場における量と等しいと思います(これについては以前にも書き込みがあります).では,電磁波としてエネルギーが発散するというのが現実(コンデンサーが絶対に壊れない仮定で)に起こるべき現象ということでしょうか?
Re: 皆さんありがとうございます!
tomo さんのレス (2005/02/11(Fri) 01:22)
みなさん,こんばんは.tomoです.
> 初めからコンデンサの電位差がVだとは考えられません.
それはそうですね.私がNo.4146で,ボッシュさんの疑問を代弁した時に, 起電力Vの電池と書きましたので,電池の起電力はVとします. コンデンサーの電位差は充電前は0ですが,電池の+極と-極の電位差はVです.
> 何故,このような複雑な状況下で,「QV」と計算できるのでしょうか? > 計算の仮定を教えてください.
コンデンサーが充電される時,電荷は極板Aから極板Bへひょいっと飛んでいくわけではありません. 極板Aにつながれた導線〜電池〜極板Bにつながれた導線〜極板Bという経路をたどります. No.4231の?のところで,Mathmatica3000さんはここを勘違いされているのではないでしょうか. Mathmatica3000さんの記述を見ると,電荷が持ち上げられるべき電位差は, その時のコンデンサーの極板同士の電位の差であるように受け取れます. そうではないですよね.極板同士は導線でつながっているわけではないのですから, 極板Aから極板Bへ,電池を通らずに移動することはできません.
電池は,電位差Vだけ,電荷を持ち上げることになります.従って,電池のした仕事はQVとなります.
充電された時,コンデンサーは静電エネルギーQV/2を持っています. 電池のした仕事の半分ですね.残りの半分は導線で発生したジュール熱だと思います. エネルギー保存は成り立っています.
Re: 皆さんありがとうございます!
Mathmatica3000 さんのレス (2005/02/11(Fri) 09:36)
>最終的に落ち着いたときにコンデンサーに溜まるのは静電場における量と等しいと思います.
コンデンサに貯まるエネルギーの量は
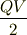
と導きましたが,正確にはこの表式は,静電場のときだけ正しい式です. 電場が時間的に変化する,より一般の式に関しては,より一般の状況を考えて,書き直す必要があります. 書き直した形は,単位体積当たりのエネルギーとして
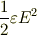
という形に書き換えられます(ご存じだと思いますが).
確かに,最終的にコンデンサに貯められるエネルギーは等しいでしょう. しかし,電磁波の発生・静電場が乱されるということからすれば,「エネルギー収支」としては成り立っていないだろうし,またこの議題から逸脱する,と考えられます.
>コンデンサーが充電される時,電荷は極板Aから極板Bへひょいっと飛んでいくわけではありません.
その通りです.ひょいっと飛んでいくわけではありません. しかし,私は静電的(準静的)という「ものすごく特別な」場合について説明しました. このとき,グラジエントの積分定理から,仕事は経路に依りません. だから,「静電的(準静的)という仮定がある」限り,上の計算は正しいのです.
Re: 皆さんありがとうございます!
Mathmatica3000 さんのレス (2005/02/11(Fri) 09:51)
>それから後,コンデンサーがなされる仕事が電池のする仕事に等しいことを示さなければこの問題に答えたことにはなりません.
何度も言うように,この場合は「静電的」という「ものすごく特別な場合」です. 電磁波の放射がない(ダイナミックでない)ものすごく特別な場合です. 従って計算の過程も,静電的な仮定を守らなければなりません. そこまで電池にこだわるならば,静電的という仮定を守れる「ものすごく理想的な電池」を考えなければならないし,そんなものは現実にはありません.
tomoさん >電池は,電位差Vだけ,電荷を持ち上げることになります.従って,電池のした仕事はQVとなります. では電位差Vができあがっている段階(電荷を持ちあげる以前)の,コンデンサの静電場のエネルギーは,いくらですか?
Re: 皆さんありがとうございます!
崎間 さんのレス (2005/02/11(Fri) 10:33)
> 従って計算の過程も,静電的な仮定を守らなければなりません. > そこまで電池にこだわるならば,静電的という仮定を守れる > 「ものすごく理想的な電池」を考えなければならないし, > そんなものは現実にはありません.
その場合は,電池のした仕事とコンデンサのエネルギーの差異 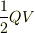 もなくなるのですね.考えていた現象に,少しずつすれ違いがあったような気がします.
もなくなるのですね.考えていた現象に,少しずつすれ違いがあったような気がします.
Re: 皆さんありがとうございます!
おこめ さんのレス (2005/02/11(Fri) 11:42)
>そこまで電池にこだわるならば,静電的という仮定を守れる「ものすごく理想的>な電池」を考えなければならないし,そんなものは現実にはありません.
電池にこだわるのでなく,問題がそれだからです.だれもコンデンサーに溜まるエネルギー,電磁波の発生を問題にしていないということです.現実に起こるかどうかの段階の話をしていないことにも注意が必要です(基本的仮定を守る範囲で話をしてます).
もし現実に起こるべき現象について述べるのであれば,もう一度こうこうこういう理由で電磁波が発生し,ジュール熱はこれだけ発生する.コンデンサーに溜まるエネルギーはこうなる.というように説明されなければ誰もついてこないと思いますよ.根本的に話題としている事が違うように思います.
導線から電磁波発生するときの電流は当然定常電流でないということですね. ∇・j≠0でないと電磁波など発生しないです.これはオームの法則の発散をとれば分かります.次にコンデンサーから電磁波が発生するという事が考えられそうです.これについては考えた事が無いので分かりません.
少なくとも僕はそのような話をしているつもりはありませんでした.実際にこのような問題を考えるときは電流は与えられなければ解決不可能にも思いますが,解析可能なのですか?
Re: 皆さんありがとうございます!
Mathmatica3000 さんのレス (2005/02/11(Fri) 12:46)
話題は同じです. コンデンサの静電エネルギーというのは,コンデンサを充電するために必要なエネルギーのことですよね. ただし,これにはスタティックな,静電的な,という条件が付加します.
>導線から電磁波発生するときの電流は当然定常電流でないということですね. ∇・j≠0でないと電磁波など発生しないです.これはオームの法則の発散をとれば分かります.次にコンデンサーから電磁波が発生するという事が考えられそうです.
その通りです. しかし初めの状態では,コンデンサは充電されていなく電位差も発生していないため,充電する過程で過渡的な状態を経なければなりません. この過渡的な状態が,静電的という過程に反するのです. だから,静電的に仕事を出来るような仮想的な電池が必要だ,と私は言っているのです.
静電エネルギーが 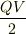 となるのは,静電的な場合に限られます.
そこに何故,電池という動的な,相容れないものを持ってくるのです?
となるのは,静電的な場合に限られます.
そこに何故,電池という動的な,相容れないものを持ってくるのです?
Re: 皆さんありがとうございます!
tomo さんのレス (2005/02/11(Fri) 12:51)
みなさん,こんにちは.tomoです. ご指名を受けました.
> tomoさん > では電位差Vができあがっている段階(電荷を持ちあげる以前)の,コンデンサの静電場のエネルギーは,いくらですか?
電荷を持ち上げる以前のコンデンサーの静電エネルギーは0です.
スレッドの最初で,ボッシュさんが,
> こんにちわ〜初めましてボッシュと申します.大学入試で悩んでいる高校三年生です.
と書いています.私は,大学入試で悩んでいる高校3年生向けにレスをつけてきました. 崎間さんやおこめさんが指摘されているように,議論の内容に違いがあったようですね.
Re: 皆さんありがとうございます!
おこめ さんのレス (2005/02/11(Fri) 13:18)
>この過渡的な状態が,静電的という過程に反するのです.
過渡期に流れる電流は定常電流です(これはもちろん理想的にオームの法則,マクスェル方程式に厳密に成り立つとしたときです).だから静電的かどうかは判断できませんが,電磁波は発生しません.電極板に溜まる電荷からも電磁波は発生しません.このとき極板の磁場,電場はともにラプラス方程式を満たしています.
Mathmatica3000さんの発言からはI=I(t)ならば電磁波が流れるかのように取れますが,I=I(x,y,z,t)でないとまず電磁波は発生しようがありません.
過渡期に流れる電流のノイズなどを考慮にいれて,発生する電磁波についても考えろという事でしょうか?
Re: 皆さんありがとうございます!
Mathmatica3000 さんのレス (2005/02/11(Fri) 13:19)
それは違います.私のレスを,きちんと見ていただけましたか?
あなた方は「静電エネルギー」というものに「電池」という動的なものを持ち出しているため,きちんと静電エネルギー 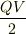 が計算できないのです.
両者は相容れないはずなのに,何故,混同して計算するのです?
電池を持ち出すこと自体が,おかしいのです.
が計算できないのです.
両者は相容れないはずなのに,何故,混同して計算するのです?
電池を持ち出すこと自体が,おかしいのです.
電位差Vが出来上がっている段階では,既に静電エネルギーは 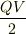 だけ,貯められていますよ.
電位差ゼロの状態から電位差Vを作り出すのに,エネルギーが必要ないわけないじゃないですか.
だけ,貯められていますよ.
電位差ゼロの状態から電位差Vを作り出すのに,エネルギーが必要ないわけないじゃないですか.
Re: 皆さんありがとうございます!
おこめ さんのレス (2005/02/11(Fri) 13:31)
交流だとしても
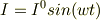
ならば定常電流です.しかしこの場合,交流にさえなりません.実際に計算してみたら分かると思います.
>電位差Vが出来上がっている段階では,既に静電エネルギーはQV/2だけ,貯められていますよ.
その話は大分前に解決していると思います.誰がそれが誤りだといいましたか?
Re: 皆さんありがとうございます!
Mathmatica3000 さんのレス (2005/02/11(Fri) 14:10)
>その話は大分前に解決していると思います.誰がそれが誤りだといいましたか? No.4245でのtomoさんの発言に答えました.
では
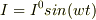 の
の  とは何ですか?
とは何ですか?
ご存じだとは思いますが,定常電流とは,強さが時間的に変わることなく流れ続ける電流です.
Re: 皆さんありがとうございます!
ken さんのレス (2005/02/11(Fri) 15:12)
kenです.こんにちは.
どうも,議論が私の中で混乱してきているので, 確認したいと思います.
まず,コンデンサー(容量C)において, その両端間の電圧がVであるとき, 蓄えられている電荷QはQ=CVであり, 蓄えられているエネルギーはQV/2である.
ここまではMathmatica3000さん,おこめさんはもちろん 最初に質問された高校生のボッシュさんをはじめどなたにも 異論はないわけですね. しかし,Mathmatica3000さんは,これが成り立つのは「静電的」 な場合に限られるという条件を加えていますね. そこでMathmatica3000さんにお尋ねしたいのは「静電的」 という条件が崩れた場合にコンデンサーに蓄えられた エネルギーがQV/2ではなくなるということがありえるのでしょうか. ありえるとしたらどのような場合でしょうか?
さて,コンデンサーに電荷をためる方法として,電池をつなげた場合
にどのようになるかということです.
Mathmatica3000さん以外は最初に質問されたボッシュさんや私を含め
電池が行った仕事はQVであると算出しています.
電池が行った仕事とコンデンサーに蓄えられたエネルギーの差が
どこにいったのかわからないというボッシュさんの質問に対して
Mathmatica3000さん以外は抵抗成分にジュール熱として奪われたという
説をとっています.(もっとも私は,では抵抗が0の理想的な場合は
どうなのだという思考実験をなげかけましたが)
Mathmatica3000さんは
「「電池」という動的なものを持ち出しているため,きちんと静電エネルギー
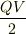 が計算できない.
静電エネルギーが
が計算できない.
静電エネルギーが 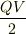 となるのは,静電的な場合に限られます.」という記述があるのみで動的なものを持ち出した場合の記載はありません
おそらく,Mathmatica3000さんはもとの質問が「電池」という動的なものを持ち出し
た場合にエネルギーが保存されないのはなぜかという趣旨なのに,質問の意図を取り違えて,「エネルギーが保存されるのは静電的な場合に限られる」としか述べていないのではないかと思います.
「エネルギーが保存されるのは静電的な場合に限られる」と言うことは,間接的には
「動的な場合はエネルギーが保存されない」と言っているのと同じなのでしょうが
なぜ,「動的な場合はエネルギーが保存されない」のでしょうか.
となるのは,静電的な場合に限られます.」という記述があるのみで動的なものを持ち出した場合の記載はありません
おそらく,Mathmatica3000さんはもとの質問が「電池」という動的なものを持ち出し
た場合にエネルギーが保存されないのはなぜかという趣旨なのに,質問の意図を取り違えて,「エネルギーが保存されるのは静電的な場合に限られる」としか述べていないのではないかと思います.
「エネルギーが保存されるのは静電的な場合に限られる」と言うことは,間接的には
「動的な場合はエネルギーが保存されない」と言っているのと同じなのでしょうが
なぜ,「動的な場合はエネルギーが保存されない」のでしょうか.
Re: 皆さんありがとうございます!
おこめ さんのレス (2005/02/11(Fri) 15:32)
>ご存じだとは思いますが,定常電流とは,強さが時間的に変わることなく流れ続ける電流です.
ああ確かに,tに依らない電流を定常電流,tに依る電流を準定常電流とも言いますね.tとはもちろん時間の事です.しかし名称の事は別にこの問題の本質ではありません.大事な事は回路の外へ電磁波としてエネルギーが逃げるかどうかという事です.I=I(t)のときも∇・J=0ですから電磁波など発生しません. 準定常電流の事を僕が定常電流と言っていたことは厳密でないかもしれません.
Mathmatica3000さんの考える動的とは変動する場とは違います.もし電池のする仕事に不満があるのならば抵抗の非常に小さな起電力一定の電源と考えてください(電池の性質などに詳しくありません).今までの話し合いではそういう認識で話は進んでいると思います.
kenさんへ 僕はkenさんの考えた思考実験に対するコメントをNo.4196でしています.できたら感想を聞かせてください.
Re: 皆さんありがとうございます!
ken さんのレス (2005/02/11(Fri) 15:58)
kenです.
おこめさんこんにちは
>kenさんへ >僕はkenさんの考えた思考実験に対するコメントをNo.4196でしています.できたら感想を聞かせてください.
すいません,正しい答えで新たにコメントを追加することはなかったので, そのままにしていました.謝辞だけはいれるべきでしたね. 別の議論が流れていたので口をはさまずにいました.
ついでに,
コンデンサーに流れる電流Iは内部抵抗を加味した元で
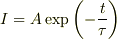 とかけますが,
これは,回路理論の過渡現象として扱われるので,私としては
定常電流や準定常電流という表現は違和感を感じるものです.
私の専門が電子回路であまり電磁気を扱わないからというのもありますが.
とかけますが,
これは,回路理論の過渡現象として扱われるので,私としては
定常電流や準定常電流という表現は違和感を感じるものです.
私の専門が電子回路であまり電磁気を扱わないからというのもありますが.
Re: 皆さんありがとうございます!
おこめ さんのレス (2005/02/11(Fri) 16:11)
そうでしたか,全く誰からも応答が無いので不安でいました.どうも感想をかいていただき,ありがとうございます.
>私としては定常電流や準定常電流という表現は違和感を感じるものです.
僕は回路などほとんど考えた事の無い人間です.僕はただ∇・j=0,∇×E=0を定常電流と呼んでいた.そういう意味でしか僕はこの言葉を使っていません.定常電流の定義としては正しくないかもしれません.いままでの僕が使っていた定常電流という言葉を ∇・j=0,∇×E=0を満たす場の電流 と読み替えていただければいいと思います.
あ,この意味でもこの場合の電流は定常電流ではないかもしれません.考え直してみます.
Re: 皆さんありがとうございます!
CO さんのレス (2005/02/11(Fri) 16:23)
ε=(@×@)ふぅ
落ち着いて読むと,mathematica3000さんは「静電気学」をやっていて,他の人たち(私も含む)は「回路理論」をやっているように見えます.
mathematica3000 さんは,コンデンサが電圧  を持っているならば,それは
を持っているならば,それは 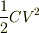 のエネルギーを持ち,静電気学的に考えれば静電エネルギー(*)は
のエネルギーを持ち,静電気学的に考えれば静電エネルギー(*)は 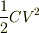 の仕事で蓄えられるのだ,と主張しているようです.それは正しいと思います.
の仕事で蓄えられるのだ,と主張しているようです.それは正しいと思います.
いっぽう,その他の人は「電池とコンデンサ(と抵抗)」を使うことを前提として話をしています.つまり回路理論と過渡現象をもとに話をしているのです.この場合に,過渡的な過程を経て,コンデンサに最終的に静電エネルギー(*) 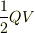 が蓄えられ,ジュール熱としてさらに
が蓄えられ,ジュール熱としてさらに 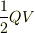 が発生する,という話も正しいと思います.
が発生する,という話も正しいと思います.
ここに食い違いがあるのではないかと思いました.
(*) 電荷分布が持つエネルギー,という意味です.
Re: 皆さんありがとうございます!
Mathmatica3000 さんのレス (2005/02/11(Fri) 16:39)
まずCOさん, >落ち着いて読むと,mathematica3000さんは「静電気学」をやっていて,他の人たち(私も含む)は「回路理論」をやっているように見えます. 落ち着くも何も,此処では「静電エネルギー」を議論しているのではないですか? 静電エネルギーは,文字通り静電学ですが,あなたは何故,動的な電池を考慮しているのですか?
つぎにkenさん,貴方は私の主張を理解してくれていません.
>Mathmatica3000さん以外は抵抗成分にジュール熱として奪われたという説をとっています.
わたしはジュール熱などと言う言葉は使ってさえいませんよ.
と言うか奪われるなんて言いましたっけ?
>「静電エネルギーが 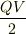 となるのは,静電的な場合に限られます.」という記述があるのみで動的なものを持ち出した場合の記載はありません
動的な場合と,静電的な場合とは相容れません.
静電エネルギーに,何故動的な説明が必要なのですか?
となるのは,静電的な場合に限られます.」という記述があるのみで動的なものを持ち出した場合の記載はありません
動的な場合と,静電的な場合とは相容れません.
静電エネルギーに,何故動的な説明が必要なのですか?
Re: 皆さんありがとうございます!
おこめ さんのレス (2005/02/11(Fri) 16:45)
Mathmatica3000さんへ ジュール熱についてのところからも感じられるのですが,あなたはよく返信内容をよんでいません.また,以前の話し合いについてもよく把握されていない.よく読んでから返信をお願いしたいと思います.あとあなたは主張を皆さんに理解してもらうのではなく理解させる必要があります(もちろん不満があるならばの話です).具体的な計算を示さない限りずっとこの状態が続きそうです.
Re: 皆さんありがとうございます!
Mathmatica3000 さんのレス (2005/02/11(Fri) 16:49)
最後におこめさん,電流の本質は電荷の移動ですね. 電荷が移動すると,一般には電磁波が発生しますね.
定常電流の場合は時間的変動が無く, 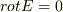 が成り立つので,電磁波の放射がありません.
が成り立つので,電磁波の放射がありません.
ところが時間的に変動する場合は, 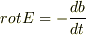 なので,電磁波の放射があります.
なので,電磁波の放射があります.
二つの場合ともマクスウエル方程式から言えます. この違いが私の言う,静的と動的の相容れないところうの根拠です.
コンデンサを充電するには過渡期を経なければ成りません.これは動的です. 今話題にしているのは「静電エネルギー」ですね. これは言うまでもなく,静電学の範疇です.
Re: 皆さんありがとうございます!
おこめ さんのレス (2005/02/11(Fri) 16:55)
電荷の移動が電磁波の発生ではありません.電荷が加速度をもって移動する必要があります.もう一度言いますが,あなた一人異論を唱えているわけです.その意見を通すためには具体的な計算を一から全て示す必要があります.あといっこ前の発言も返信として不自然な事にまだ気づきませんか?
Re: 皆さんありがとうございます!
CO さんのレス (2005/02/11(Fri) 16:57)
>> 落ち着いて読むと,mathematica3000さんは「静電気学」をやっていて,他の人たち(私も含む)は「回路理論」をやっているように見えます. > 落ち着くも何も,此処では「静電エネルギー」を議論しているのではないですか?
一番最初の出だしは,ボッシュさんの発言, 「納得いかない現象があります.それは,コンデンサーの静電エネルギーと電池のする仕事との関係です!」 です.コンデンサーの静電エネルギーと電池のする仕事との関係について議論しています.
> 静電エネルギーは,文字通り静電学ですが,あなたは何故,動的な電池を考慮しているのですか?
充電が完了した状態では電荷の移動はないですし,静電的ですよね.このときにコンデンサーに蓄えられているエネルギー,これを静電エネルギーと呼んでいます.これに問題がありますか?
Re: 皆さんありがとうございます!
Mathmatica3000 さんのレス (2005/02/11(Fri) 17:01)
返信が不自然になってしまったのは,時間をおいて更新せずに投稿してしまったからです. 気に障ったのならば,すみませんでした.
>電荷が加速度をもって移動する必要があります.
電流が時間的に変動したとします.あたたの言う
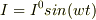 という時間的に変動する電流を考えたとします.
時間的に変動する電流は,あっち行ったりこっち行ったりの加速度運動する電荷の集団です.
という時間的に変動する電流を考えたとします.
時間的に変動する電流は,あっち行ったりこっち行ったりの加速度運動する電荷の集団です.
すなわち,時間的に変動する電流が,電磁波を放射する理由です.
Re: 皆さんありがとうございます!
Mathmatica3000 さんのレス (2005/02/11(Fri) 17:04)
そしてCOさん,
「静電エネルギーの表式は,電池を使った動的な過程とは相容れない」というのが私が最も言いたい事なのです.
従って 「静電的という仮定をいったん置いたなら,動的な過程を考えてしまうのは,おかしいじゃないか」 と言う事を言いたいのです.
わかりにくかったらすみませんでした. 申し訳ありません.
Re: 皆さんありがとうございます!
おこめ さんのレス (2005/02/11(Fri) 17:08)
>>Mathmatica3000さん以外は抵抗成分にジュール熱として奪われたという説をと>っています. >わたしはジュール熱などと言う言葉は使ってさえいませんよ. >と言うか奪われるなんて言いましたっけ?
僕はここの部分を言っています.
電流についてはホントに電磁波が発生するのならばどこからどのような電磁波が発生するのか式で示してください.
Re: 皆さんありがとうございます!
Mathmatica3000 さんのレス (2005/02/11(Fri) 17:12)
式では私の実力では出来ません. しかし,変動する電流が電磁場を発生する事は,現実に実用化されています.
おこめさんは,アンテナ電流はご存じですか? テレビの送受信や携帯電話などで,電波の送受信に使われる原理です. グーグルで検索してみるといいです.
Re: 皆さんありがとうございます!
おこめ さんのレス (2005/02/11(Fri) 17:19)
電源部分がそのようになっている事も考えられるでしょう.分からなかったと思いますが,僕は導線から電磁波は発生しないといっただけの事です.これは完全な説明不足でした.またこの考えが正しいとも限りません.この意見の拠り所は Iをある特定の向きを取っているのでその電流の発散をとればゼロになる.だから導線からは電磁波などでませんよ.そういうことです.これについては話の混乱になるだけなので,以下話に出さないようにお願いしたいと思います.ホントに気になる人が計算すればいい事ですから.
数式が示されなければいかなる憶測も意味を持ちません.哲学など持ち込むのはもっと意味がありません.だから数式で示さなければならないのです.それができなければ主張を通す事は不可能だと思います.実力では無理ではなくやった事がないだけでしょう.ある仮定の元に計算を進めればその仮定の範疇で正しい結果が出てきます(数学的に同値なので当たり前の事ですが).
Re: 皆さんありがとうございます!
ken さんのレス (2005/02/11(Fri) 17:30)
kenです. (レスポンスが遅く,前の話に戻ってしまいますが,)
Mathmatica3000さんの No.4257 について >つぎにkenさん,貴方は私の主張を理解してくれていません. >>Mathmatica3000さん以外は抵抗成分にジュール熱として奪われたという説をとっています. >わたしはジュール熱などと言う言葉は使ってさえいませんよ. >と言うか奪われるなんて言いましたっけ?
そりゃそうでしょう.私も「Mathmatica3000さん「以外は」...説をとっています.」 と書いたのであって,「Mathmatica3000さん「は」...説をとっています.」 とは書いていないですから. 話を逆にしないでください.ただでさえ,話が混乱して,まとめようとしているところに逆に解釈されたら,よけいに混乱してしまいます.
>>「静電エネルギーがfrac{QV}{2}となるのは,静電的な場合に限られます.」という記述があるのみで動的なものを持ち出した場合の記載はありません >動的な場合と,静電的な場合とは相容れません. >静電エネルギーに,何故動的な説明が必要なのですか?
>従って「静電的という仮定をいったん置いたなら,動的な過程を考えてしまうのは,おかしいじゃないか」
そもそも議論の内容は動的な過程の話であって,静電的という仮定をおいたことは ないからです.したがって,先の質問も,動的な場合はどうですかと たずねているわけです.
Re: 皆さんありがとうございます!
Mathmatica3000 さんのレス (2005/02/11(Fri) 17:45)
具体的な計算は, 物理学テキストシリーズ電磁気学砂川重信著 のp305にありますね. そこでは,具体的に長さdのアンテナを考え,変動する電流が流れているとし,ポインティングベクトルから電磁波が運ぶエネルギーを計算しています.
Re: 皆さんありがとうございます!
Mathmatica3000 さんのレス (2005/02/11(Fri) 18:02)
kenさん,大変申し訳ありませんでした.これは全く私の読み間違いです.
確かに,最終状態(電位差Vで落ち着いた状態,これは完全に静電的ですね)では, 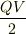 なるエネルギーが蓄えられます.
しかし過渡期を経ると,今おこめさんに説明しているように,電磁波が発生してエネルギーをどこかに運んでいってしまいます.
これが,ロスな訳です.
なるエネルギーが蓄えられます.
しかし過渡期を経ると,今おこめさんに説明しているように,電磁波が発生してエネルギーをどこかに運んでいってしまいます.
これが,ロスな訳です.
それ以前の問題として,電池を使った動的な場合を例にいいましょう. はじめにコンデンサには電位差は発生していませんね.過渡を経なければ成りません. このような状態では,電磁波の放射のようにかなり様相は複雑です. したがって「電池の起電力Vとすると,仕事はQV」と単純にする事は出来ないのです.
説明の順序が悪くてすみません. 初めからこういえばよかったかもしれません.
後もう一つ,おこめさん 電源部分から電磁波がが発生しているだと貴方は言いますけど,電源だって変動する電流が流れているわけです. しかもアンテナは電源に接続されている必要はありません. 検流計につなげばいいだけです.
そして「私の実力では無理」と言う事であって,もっと以前にこのことをきちんと計算している人はきちんといます. 上にも挙げましたが.
Re: 皆さんありがとうございます!
おこめ さんのレス (2005/02/11(Fri) 18:27)
そのような記述はしていません.電源部分がコイルになっていて外部からの電磁波を吸収する場合を言ったつもりでした. 電磁波の話題はださないようにお願いしたつもりでしたが,電磁波によってロスすると考えていたのですか.参考書をもってらっしゃるのならば計算を示してください.僕の答えとはかけ離れています.電源の起電力はEで一定ですよ.
僕たちが話し合っているのはRC回路です.LRC回路ではありません.ここを勘違いされているように感じます.
それから電磁波は砂川さんではなくもっとずっと昔に解決された問題です.しかも引用されている問題とここでの話は関係ないと思います.適用して示してください.
Re: 皆さんありがとうございます!
Mathmatica3000 さんのレス (2005/02/11(Fri) 18:41)
電磁波の話題を出すも何も,私は電磁波の発生との関連をずっと述べているんですよ.
計算を示す事には意味があまり無いのではないですか? 実際にそのことを計算した人がいる,その様な導出がある,貴方の言う数式は存在する,と言う事は確かなのです. 電流が流れる導線から電磁波の放射が変動することをが確認されたのは,その数式の存在から明晰判明です.
あなたは「ネットでを調べるより,大学の図書館へ向かったほうが早く,正確な答えが得られると思いますよ」と以前この掲示板でおっしゃっていましたね(質問者が化学系の人だったやつです).
ご自分で明日,確認されたらどうですか?
Re: 皆さんありがとうございます!
Mathmatica3000 さんのレス (2005/02/11(Fri) 18:46)
以前にも書き込みをしましたが,
はじめにコンデンサには電位差は発生していませんね.過渡を経なければ成りません. このような状態では,電磁波の放射のようにかなり様相は複雑です. したがって「電池の起電力Vとすると,仕事はQV」と単純にする事は出来ないのです.
Re: 皆さんありがとうございます!
おこめ さんのレス (2005/02/11(Fri) 18:48)
その必要はありません.ここで述べられている問題については教科書レベルの解析なら自分でできるからです.また教科書も所有しています.
Re: 皆さんありがとうございます!
Mathmatica3000 さんのレス (2005/02/11(Fri) 18:50)
では電池のする仕事をお示し下さい.
Re: 皆さんありがとうございます!
おこめ さんのレス (2005/02/11(Fri) 19:02)
Mathmatica3000さんが唯一奇抜な発想をお持ちなようなので数式で示してほしいと書き込んだだけです.それは全くせずにほぼ共通認識として落ち着いていることをわざわざ数式で書き込めとそういうことですか?
Re: 皆さんありがとうございます!
Mathmatica3000 さんのレス (2005/02/11(Fri) 19:15)
その通りです. コンデンサーを電池で充電する過程で,いくらの仕事をするか,示してください.
Re: 皆さんありがとうございます!
Mathmatica3000 さんのレス (2005/02/11(Fri) 19:18)
だいたい私は「コンデンサを充電する過程で,電池のする仕事を計算し,表式するのはとてもむづかしい」ということを言っています. 私には出来ません,あなたがやってみて下さい.
Re: 皆さんありがとうございます!
おこめ さんのレス (2005/02/11(Fri) 19:32)
E:起電力,I:電流Q:電荷 w:単位あたりに電池がする仕事(消費電力) 天下り的に次の公式を与えます. Q=∫Idt w=EI 消費電力wを時間積分して仕事Wを計算します. W=∫EIdt=E∫Idt=EQ 以上です.
Re: 皆さんありがとうございます!
とおりすがり さんのレス (2005/02/11(Fri) 19:48)
まあまあみなさん,この話題はしばらくお休みにしませんか. ちょっと時間をおいてからもう一回やってみるとかにして. (私はウエットな日本人なので,キツイ会話は苦手.特技は先送り)
Re: 皆さんありがとうございます!
Mathmatica3000 さんのレス (2005/02/11(Fri) 19:52)
そんな簡単にはいきません. それは定常電流についてでしょう.過渡的な状況も考えましたか?
Re: 皆さんありがとうございます!
おこめ さんのレス (2005/02/11(Fri) 19:55)
Eは一定ですよ.それとも公式が誤りと言いたいのですか? 砂川さんの本には回路の問題は載っていないのですか(RC回路を調べてください.googleでも答えは見つかるでしょう.)?もう少し考えてからどこがおかしいのか示さなければ話し合い(みなさんは議論とおっしゃる)は成立しません.
これ以上の質問は別にスレッド(この用語であってるのか分かりませんが)を立ててください.
Re: 皆さんありがとうございます!
Mathmatica3000 さんのレス (2005/02/11(Fri) 19:59)
過渡的な状況では電流が変化するので,電磁誘導による自己誘導起電力が発生します. その分はどうして考えてないのですか? 定常電流と,時間的に変動する電流は,取り扱いが全然違いますよ.
Re: 皆さんありがとうございます!
おこめ さんのレス (2005/02/11(Fri) 20:02)
だからそれはLRC回路(自己誘導などを起こすのはコイルのところだと記憶しています.しかし正確な事は別にまた考えなければなりませんので正確でない可能性があります)など他の問題の話でしょう.これ以上の質問は別にスレッドを立てていただけませんか?
Re: 皆さんありがとうございます!
nanotube さんのレス (2005/02/11(Fri) 21:25)
はじめまして,みなさんこんぬづわ!
よこやり失礼します. 回路理論というのを全く知らないのですが(汗),私の記憶では大学受験ではあくまでも理想的な回路を扱っていたので,ジュール熱などは考えなかったような気がします・・・ 起電力Vによりコンデンサーの片側からもう片側へ1/2QVが送られるため,(理想的な)電池のなした仕事が1/2QVであるっ!というわけにはいかないんですか?
Re: 皆さんありがとうございます!
おこめ さんのレス (2005/02/11(Fri) 21:36)
どうもはじめまして,nanotubeさん.このような書き込み,それにたいする考察などは以前にされています.当然そのようにこの問題は片付ける事はできますね.余裕があればどこにそのような事が書いてあるか探してみてください.