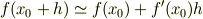テーラー展開
テーラー展開
やかん さんの書込 (2005/02/06(Sun) 10:20)
高校では習ったような習わなかったようなテーラー展開ですが，どうも書籍の説明がムズイものが多く，私好みの柔らかい説明をしてるサイトがありましたので御紹介します（私自身完全にサイトの内容をまだ吟味できていないので悪しからず）．掲示板の読者でご参考になられる方がいらっしゃれば幸いです．
Re: テーラー展開
かつ さんのレス (2005/02/06(Sun) 12:18)
関数 f(x) の点 x 0 の周りでの展開を考えます． テイラー展開を一階で打ち切ると f(x 0 +h)≒f(x 0 ) + f'(x 0 ) よって f'(x 0 )＝f(x 0 +h) - f(x 0 ) h が十分に小さい時，これは点x 0 における微係数の定義
・・・と考へれば，直感的に解ったやうな気になる・・・かも？？
Re: テーラー展開
かつ さんのレス (2005/02/06(Sun) 19:40)
あ，これは失礼(A^^;)．ミスでした．ご指摘有り難う御座います．＞COさん
Re: テーラー展開
たかひと さんのレス (2005/02/07(Mon) 01:18)
やかんさん，こんばんわ．院浪人のたかひとと申します． 貼られたリンクからサイトを閲覧しました．世の中にはこんな先生もおられるのだな，というのが感想です．テーラー展開の説明の他にも，たたみこみの説明を読み，爆笑しました．おもしろい！且つ解りやすい．数学（解析学）は，日常ではあまり使われないからこそ，日常に存在する事柄を取り上げて説明するのが良いのではないかと思いました．
良いサイトを教えていただき，ありがとうございます．失礼します．
Re: テーラー展開
しん さんのレス (2005/02/07(Mon) 14:55)
ああ，テーラー展開だ！
>柔らかい説明をしてるサイトがありました とても分かりやすいですね．
剛体シミュで数値積分を実装時に，"基礎となる理屈"としてお世話になりました． 「誤差はあるけど，十分使えるよ！」っていう強引な所が，私にぴったりです．
Re: テーラー展開
やかん さんのレス (2005/02/07(Mon) 17:18)
＞かつさん ＞ＣＯさん あっ，ほんとだ，極限というか，微分の定義式みたい． うーん，お蔭様で納得できた気になりました！ :) （そうすれば２次以降も同じ論法でいけるのかな． ちょっと考えてみます）
＞たかひとさん ホント面白くてわかりやすいですよね． きっとこの先生，学生になんとしてもわかってほしいと， 頑張ってらっしゃるんでしょうね．きっと私が学生だったら 調子に乗って何回も聞きに行っちゃうかも．
＞しんさん 確か私が高３の時，数学の先生が黒板にテーラー展開書いて，”これが載ってないなんて 駄目な教科書だなあ”なんておっしゃってたのを覚えています． 大学受験は結局展開理解しないまま終わってしまい，なんか難しいもの，という記憶しかなかったのですが，こういうわかりやすい説明はリバイバル学習には大変助かります．
Re: テーラー展開
やかん さんのレス (2005/02/08(Tue) 12:33)
やかん＞ ＞（そうすれば２次以降も同じ論法でいけるのかな． ちょっと考えてみます）
なんか私勘違いしてました．すみません・・．
先日のURLで，本文中に引用されている部分積分を使った方法，かろうじて部分積分の公式を覚えていた身には，これもしっくりくるような気がしました（１個所1/2が抜けてますね）．
Re: テーラー展開
崎間 さんのレス (2005/02/08(Tue) 23:28)
やかんさんご紹介のページ，どちらも分かりやすいですね．とくに
は目からウロコです．いろいろな方が，Webでいろいろな説明を書いておられますねー．分野別にまとめてリンク集をこしらえたいものです :)
Re: テーラー展開
やかん さんのレス (2005/02/10(Thu) 02:21)
崎間さん，こんにちは！
＞やかんさんご紹介のページ，どちらも分かりやすいですね
ホント，私が読んでわかるのですから，相当のわかりやすさです． 高校時代，インターネットがあったらなあ．でもあったらあったで 勉強調べないでゲームばっかりやってたりして・・．やっぱこれで良かったのかも (^^;
