いましん（大学１年生） さんの書込 (2005/01/31(Mon) 01:36)

gradとdivはどう違うのでしょうか？どちらも，偏微分を表しているようで，同じにみえるのですが…．わかりやすい解説をお願いします．

ひろき さんのレス (2005/01/31(Mon) 03:48)

初投稿の後に失礼します． もし私の書いたことが間違っていたらどなたか指摘を御願いします．

言葉で説明すると，gradという演算はあるスカラー場の傾きのことです． スカラー場とはたとえば静電ポテンシャルや中心力ポテンシャルなどだと思えばよいと思います． つまりポテンシャルを表す関数が与えられていればそのポテンシャル上のどの位置でどのくらいの傾きがあるかがわかるわけです．

gradはポテンシャルのようなスカラー場に対して適用されますが，divは発散といってベクトル場に対して使う演算です．そのベクトル場に発散の傾向があるかどうかを調べるのに使います． たとえば一つの正電荷の電気力線を描いてみてください正電荷から外側に向かって広がるように矢印を描くことが出来ると思います．なんとなく”発散！”って感じがしませんか？電気力線は電場と同じ意味なので電場というベクトル場は発散の傾向を持っています．現に div<b>E</b>=ρ/ε ₀ という式が電磁気学にはあり，電場の“発散の傾向”が0ではないということがわかります． ここからガウスの法則や磁場の渦無しの法則を語ることが出来ますが．それは教科書で勉強してください．(とても説明できる量ではないので)あと流体力学なんかにも出てくるので，ちょっと読んでみるといいと思います．

ちなみにこの説明はあくまでgradとdivの私の理解の仕方を書いたものなので，是非教科書を読み返してもう一度確認していただきたいです．

ひろき さんのレス (2005/01/31(Mon) 03:53)

P.S 初めて訪問したのに，長々と説明してしまってすみません．>管理者の方

おこめ さんのレス (2005/01/31(Mon) 06:55)

ひろきさんの言うようなイメージはだいたい流体のような視覚的なイメージですが，保存する物理量は物理量（ベクトル）の時間変化が物理量の時間変化の位置依存性（多くの場合流れと呼ぶと思います）のdivに等しいという形にまとめることができると思います．gradは別にスカラー場，ベクトル場に限らず定義できますよ．僕はあまりこの表示は好きでないので∇と∇・で書きます．このほうが演算規則が分かりやすいです．あと計算のときに列ベクトルを使うと，もっと計算が楽になりますよ．

あとgradはベクトル関数でも定義できて，成分は行列表示で３行３列になります（２かいのテンソルというのでしたっけ）．divのスカラー関数はgradに等しくなります．なのではじめに書いた保存の形を示していると思っていただいても結構ではないかと思います．

∂/∂tF＝−∇・GF：物理量G：物理量の流れ

div,gradはどちらも位置勾配に関係した量（divは勾配総量，gradは勾配を成分に分けて表示）と考えても良いと思います．

ここからは特に自信はありませんが，gradは独立でない物理量のそれぞれの位置成分（つまりラグランジェ的な見方）の結合則を一次元下の関数で表す時に使う．divはテンソル場をそれぞれの物理量の流れの成分に分割して考えるときに使う（これを更にgradを用いると１次元下の[ナブラのダイアド-ラプラシアン]のかかったテンソルのポテンシャル？に帰着できる）．このとき一次元あがる． と考えることができそうです． あとdivの場合，体積積分すると面白いことが分かりますよ．

でもまずはベクトル関数のdiv演算はスカラー関数，スカラー関数のgrad演算はベクトルだということから徐々に慣らしていきましょう．考えるより使って慣れるのがいいかもしれません．

やかん さんのレス (2005/01/31(Mon) 18:28)

いましんさん，はじめまして．私はベクトル解析好きな割にいまだにちゃんとわかってない（grad＝山登りの一番きつい向きときつさ，div＝温泉の湧き出し，rot＝渦潮，ぐらいの乏し〜いイメージです）ので，ひろきさんや，おこめさんの説明がとても勉強になります．私は人に説明するなぞできないので関連のＵＲＬ探すぐらいしかお役に立てないのですが，以下のもご参考になりますか？

• http://www.ese.yamanashi.ac.jp/~itoyo/lecture/kisoden/kisoden1/nabla.htm

おこめ さんのレス (2005/01/31(Mon) 21:02)

僕の書き込みは不正確な上に無駄が多いので無視してください．

ひろき さんのレス (2005/01/31(Mon) 21:37)

いやいや，とても勉強になりました． ベクトル場のgradが2回のテンソルになるというのは考えたことも無かったです． >おこめさん

今まで，gradはスカラー場にしか演算しないと思い込んでましたから．目からウロコ(意味が違うかな？？)が落ちた気持ちです．

おこめ さんのレス (2005/02/02(Wed) 23:49)

行列形式で計算するときの方法を念のために書いておきますね． 列ベクトルAの転置行列をA^と書いた場合の発散は ∇・A=∇^A 勾配は ∇A =∇A^ です．

山本明 さんのレス (2005/02/03(Thu) 19:14)

＞いましんさんへ

ごく単純な言い方をしますが，

・gradはスカラー関数に作用して，ベクトルを作るものです． ・divはベクトル関数に作用して，スカラーを作るものです．

スカラー関数，ベクトル関数という言葉は大丈夫でしょうか??スカラーというのは方向を持たない量です．空間の各点でスカラー量を与えるのがスカラー関数．ベクトルというのは大きさだけでなく，方向も持っている量です．つまりベクトルにはx成分，y成分，z成分があります．空間の各点でベクトル量を与えるのがベクトル関数．

grad と div の定義をよく見てください．似ていると思われたかもしれませんが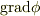， には，x成分，y成分，z成分がありますね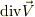． には，成分は存在していません．

どうしてこんな量を考えるのか，こういった量にはどんな意味があるのか？…という疑問に対する答えは，上でひろきさんが書かれています．参考にしてみましょう．

＃やかんさんが教えてくれたページの(eq.10)は誤植ですね． ＃右辺のi,j,kは不要です．

正確には，上でおこめさんが書かれたように，ベクトルに対するgradというのもあるんですが，それは滅多にお目に掛からないのでひとまず置いておきましょう．必要になったときに思い出してください．（私もすっかり忘れてました… (^^; ）

＞ひろきさん ご挨拶遅れましたが，はじめまして． これからもよろしくお願いしますね．

やかん さんのレス (2005/02/03(Thu) 19:27)

山本明さん，こんにちは．いつもお世話になります． ＞＃やかんさんが教えてくれたページの(eq.10)は誤植ですね． ＞＃右辺のi,j,kは不要です．

あっ，本当だ！ベクトルになっちゃってる！人にＵＲＬ紹介するときは （理解できなければともかく，これなら私レベルでも注意してればわかったはず）自分で ちゃんと内容の真偽，誤植の有無など確認してからにするべきですね．申し訳ありません．これから気をつけますm(__)m

やかん さんのレス (2005/02/04(Fri) 16:02)

以前の私のカキコミは，あんまりくだらない上に明らかに間違ってるようなので削除して，と・・， またちょっと懲りずに考えてみました（やかんの考え休みに似たり）．以前御紹介いただいた書籍”道具としての物理数学”（日本実業出版社）を読んでるのですが，とってもわかりやすくて面白いです．それに書いてあったのですが，数学の本はいきなり定義を書いて（grad=・・・，とかdiv=・・・とか），それを証明してあって，確かに厳密にあってて大丈夫だから，さあ覚えろ，使え，という感じだけど，それが発見された経緯や，どんなニュアンスを表現してるのかがわからないと全体を俯瞰できないので難しく感じる，ような事がかいてありました．その点は特に”そうそう”と変に共感しました．定義式を覚えても，どうもgradと，divのイメージが湧きずらいなあ（”湧きだし”という割には） 以前読んだ本にはスカラー関数ｆはなんでもいい（当たり前だ！）例えば，空間における温度分布．空間だから，x,y,z方向３次元あって，ｘがマイナス方向に１動くと２℃下がる，プラス方向に１動くと，２℃あがる，という時，プラスに動きゃ動くほど温度上がる，つまりｘ方向の変位に対する温度変化の割合は2÷１＝２これが∂f_x/∂x，変化率なんですね．その位置にいれば，実際に動かなくても，プラス方向に動いたら，温度あがりそう，という事です（かね？）．偏微分記号にしてるのはy,zと関係なくというだけの意味だから，横軸をｘ，縦軸をｆのｘ成分とすると，∂f_x/∂xは微分の初歩で習う，接線の傾き，これがy,z方向でも別個にあり，３つ組の要素，大きさと方向を決められるから，ベクトルに対応する，ということでしょうか？当然場所（位置座標）により，ｘのプラス方向に行けば温度下がる事もありえるから，演算の結果に変数が残っていれば（定数でなければ），位置の関数になるということですね．それにひきかえ，divの方は・・， ベクトルから，スカラーができるんだから，えーっと，この場合，∇との内積の形してるから，やっぱ内積なんでしょうね．内積って同じ方向への相乗作用を表すわけだから，x,y,zそれぞれの方向（単位ベクトルをi,j,kとか）へのベクトルの寄与というか，有効増減率，これはもちろんx(y,z)方向に変位したときの，という事だから，やはり，偏微分演算子がくっつく，その率（スカラー）を，y,zとも同じウエイトで考え，単純にたして，変位による増加率がプラスか，マイナスか，大きいか，小さいか，をあらわしたもの，それがdiv，でしょうか？だんだん，自分で言ってる事わかんなくなってきました．勝手に言葉作ってるし・・． (^^;