古典的波動方程式

ゆまともさんの書込 (2005/01/30(Sun) 00:19)

某企業で材料開発に携わっているゆまともと言います．最近，材料開発を突き詰めていくと，物理が改めて重要だと感じまして，久方ぶりに教科書をめくって勉強を始めたところです．今読んでいるのは，マッカーリ・サイモンの物理化学と言う本なのですが，この本は，私のような量子化学初学者にも非常にわかりやすく，学生時代にあればどれだけ理解が深まったかと思う一冊です．ただ，一部よくわからない点があります．

シュレディンガー方程式の対比として，古典的波動方程式が出てくるのですが，2つ固定点の間に張った振動する弦の変位をu(x,t)とすると，

d2u(x,t)/dx2 = 1/v2 * d2u(x,t)/dt2（Vは速度）

とあります．偏微分方程式なのですが，左辺と右辺がそれぞれ何を意味しているのかよくわかりません．また，なぜ2階なのでしょうか？この式が導出される前提の式があるのでしょうか？基本的な問題なのかもしれませんが，ご教示頂ければ助かります．

Re: 古典的波動方程式

おこめさんのレス (2005/01/30(Sun) 00:51)

波を表す関数の進行波と後退波が解になるような方程式が上の式（波動方程式の一つ）です．２階微分方程式なので解が２つあるのです．それ以上の意味はそれぞれの力学系によって事情が違うと思います．後言える事は左が位置による変動，右が時間発展を示しています．

Re: 古典的波動方程式

かつさんのレス (2005/01/30(Sun) 10:53)

おこめさん，横から失礼．ゆまともさん，はじめまして．

何故，2階なのかと言えば，勿論“そうなるから”ですけど・・・ :) まぁ１階じゃ共振と言うのはあり得ないですから，共振の起こる最低の階数と言えばそうですかね．つまるところ，ゆまともさんのご質問は，弦の振動の方程式をどうやって導けば良いのか？，と言う事ですか？この式を立てるのに前提となる式は，F=ma と三角関数の近似だけですね :)

Re: 古典的波動方程式

ゆまともさんのレス (2005/01/30(Sun) 13:04)

おこめさん，かつさんご返答有り難うございます．この方程式の解は変数分離法と境界条件を入れてやり，オイラーの式やt=0の初期条件などを代入してやると，

u(x,t)=cos(w1t)sin(πx/L）+1/2＊cos(w2t+π/2)sin(2πx/L）（L:固定端間距離）

となり，第1調和振動と第2調和振動の和になります．この解法は問題ありません．

かつさんご指摘のようにこの弦の振動の方程式（d2u(x,t)/dx2 = 1/v2 * d2u(x,t)/dt2（Vは速度））をどのように導出するかという点がよくわからないのです．F=ma と三角関数の近似から導出するとのことですが，どのように導出するのでしょうか？ご教授頂ければ幸いです．

Re: 古典的波動方程式

崎間さんのレス (2005/01/30(Sun) 14:32)

> F=ma と三角関数の近似から導出するとのことですが， > どのように導出するのでしょうか？ご教授頂ければ幸いです．

考えている波動媒体（たとえば弦）の微小断片に対して，質点の力学の運動方程式と同じものを立てます（図がなので分かりづらいですが，なんとか想像していただければ…）．

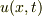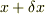縦軸に u(x,t) ，横軸にをとり，弦の微小部分 Q と Q' を考えます．Q の座標は，Q' は $x+\delta x$ とします．この断片に対して運動方程式を求めます．

断片に作用する力は，弦の張力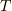と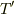で，それぞれ逆向きです．弦の断片に対する重力の効果は無視できるとし，弦の単位長さあたりの密度を $\rho$ とします．

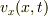断片の軸方向の速度成分を v_x(x,t) と書くと，運動方程式は

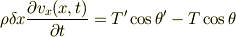
$\rho\delta x\frac{\partial v_x(x,t)}{\partial t}=T'\cos \theta '-T\cos \theta$

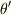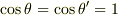と書けます．ここで $\theta$ , $\theta '$ はそれぞれ Q, Q' で弦と軸のなす角です．角度が小さいとき， $\cos\theta = \cos\theta '=1$ と近似できます．さらに，微小断片の長さ 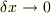$\delta x\to 0$ の極限で，上式の右辺はゼロとなるため，張力の大きさは等しく 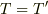T=T' として良いことになります．

ここまでが準備です．

知りたいのは，に垂直方向の運動方程式です．垂直方向の力は

$T\sin\theta ' - T\sin\theta$

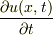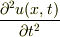となります．垂直方向の速度は $\frac{\partial u(x,t)}{\partial t}$ で表されるので，加速度は $\frac{\partial^2 u(x,t)}{\partial t^2}$ となります．したがって運動方程式は

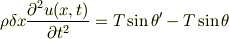
$\rho\delta x\frac{\partial^2 u(x,t)}{\partial t^2}=T\sin\theta ' - T\sin\theta$

です．このとき

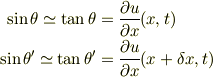
$\sin\theta \simeq \tan\theta &= \frac{\partial u}{\partial x}(x,t)\\\sin\theta' \simeq \tan\theta' &= \frac{\partial u}{\partial x}(x+\delta x,t)$

ですから，

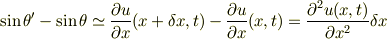
$\sin\theta'-\sin\theta \simeq\frac{\partial u}{\partial x}(x+\delta x,t) - \frac{\partial u}{\partial x}(x,t) = \frac{\partial^2 u(x,t)}{\partial x^2}\delta x$

となります．したがって運動方程式は

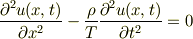
$\frac{\partial^2 u(x,t)}{\partial x^2}-\frac{\rho}{T}\frac{\partial^2 u(x,t)}{\partial t^2}=0$

になり，

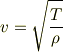
$v=\sqrt{\frac{T}{\rho}}$

の関係から，

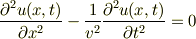
$\frac{\partial^2 u(x,t)}{\partial x^2}-\frac{1}{v^2 }\frac{\partial^2 u(x,t)}{\partial t^2}=0$

です．この微分方程式が（1次元）波動方程式です．

Re: 古典的波動方程式

かつさんのレス (2005/01/30(Sun) 15:08)

ここで書くには，図とか無いと解り難いかも知れませんが・・・努力してみます．

弦の振動は y方向のみ，弦の方向を x 軸にします．弦長を L，線密度（質量/単位長さ）をσ，張力を T として，弦が正弦波で振動している姿を想像して下さい．弦の変位と微少区間 [x, x+Δx] に働く力を Fy とすると，点 x と点 x+Δx は張力の働く方向を考慮し，張力の方向とｘ軸方向との角度をそれぞれθ，θ'として， Fy = T sinθ' - T sinθ 弦の振幅を y=u(x,t) と置きます（勿論境界条件は u(0,t)=u(L,t)=0 ですね） θ，θ' が十分に小さいとして，sinθ≒θ故， Fy/T ≒ θ'-θ = { ∂u(x+Δx, t)/∂x } - ∂u(x,t)/∂x

≒ {∂u(x, t)/∂x + Δx・∂ ² u(x,t)/∂x ² } - ∂u(x,t)/∂x ＝ Δx・∂ ² u(x,t)/∂x ²

ここで，∂u(x+Δx, t)/∂x が [x+Δx, t] での x に関する偏微分を表しています．で，この区間の弦の質量は明らかにσΔx 故，y 方向への運動方程式はF=maから σΔx・∂ ² u/∂t ² ＝T・∂ ² u/∂x ² ・Δx

後は求まるでしょう．

Re: 古典的波動方程式

かつさんのレス (2005/01/30(Sun) 15:11)

ありゃ，崎間さんとかぶっちゃいましたね (^^; 明らかに崎間さんの方が丁寧に，キチンと書かれていますので，私のは無視して下さい．

Re: 古典的波動方程式

崎間さんのレス (2005/01/30(Sun) 15:15)

かぶってしまいました，すいません．長い文章を書いていると良くこういうことがありますね (^^; でも二つあれば安心です（僕は間違いが多いので）．

Re: 古典的波動方程式

CO さんのレス (2005/01/30(Sun) 17:26)

むかし，日曜の朝早くのテレビでこんなことを言っていたのを思い出しました．「暗いと不平を言うよりも，進んで明かりをつけましょう．」

ということで，不便ながらも図を書いてみました． <pre> u(x,t) ++----------+----------+-----------+----------+-----------+-----------+----------+--------++ + + + + + + + + | | | | | ++ ++ | | | T'sinθ' | ++ ↑ ** | ｜ ********** | | ｜ ***** | | ｜ ** θ' | ++ ****____________ ++ | ** : | | * : | | * θ : | ++ *****___________ : ++ | ** ｜ : | | * ｜ : | | * ｜ : | ++ **** ↓ : ++ | **** T sinθ : | | * : : | ++ ** : : ++ | * : Q : Q' | | ** : : | + ** + + +: + : + + + | **----------+----------+-----------+----------+-----------+-----------+----------+--------++ x x x+dx </pre> うーん，いまいち・・．画像を載せられたらいいですね :)

Re: 古典的波動方程式

かつさんのレス (2005/01/30(Sun) 21:27)

>「暗いと不平を言うよりも，進んで明かりをつけましょう．」諫言，痛み入ります．m(__)m

>うーん，いまいち・・．いやいや，グラフの AA化としてはなかなか見事です． :)

Re: 古典的波動方程式

ゆまともさんのレス (2005/01/30(Sun) 21:47)

崎間さん，かつさん，COさん

大変わかりやすい解説頂き大変ありがとうございました．運動方程式を立てることがミソだったのですね．高校物理程度しかわかっていない私でも十分理解できました．もやもやが解消され，気分が良くなりました．シュレディンガー方程式で，粒子のエネルギーは量子化されており，整数nで決まることが，遡っていくとこのような古典的な弦の運動方程式に帰着するところに物理のロマンを感じます．学生時代，量子の世界はとびとびの整数の世界で，これは覚えるしかないと教えられたことを思うと，古典力学と量子力学のつながりを感じることができたのは，目から鱗です．これからもさらに理解を深めるよう進めていきたいと思います．本当に有り難うございました．

Re: 古典的波動方程式

おこめさんのレス (2005/01/30(Sun) 22:28)

>シュレディンガー方程式で，粒子のエネルギーは量子化されており，整数nで決まることが，遡っていくとこのような古典的な弦の運動方程式に帰着するところに物理のロマンを感じます．

いや非相対論的量子力学の場合，波動方程式の種類からして違いますよ．あとですね，弦の運動に帰着するのではなく，量子が波動性と粒子性を持っていると言うことです（高校の教科書にも載っていると思います．）．あと古典力学とのつながりを眺めるのならば解析力学をやると分かると思います．しかし化学にはあまり関係ないので，興味がなければあまり見る必要も無いと思います．