arc さんの書込 (2005/01/28(Fri) 17:33)

初めまして．電磁気学を勉強していたところ，分からないところが出てきたので教えてください．

「荷電粒子が加速度運動すると電磁波を出す」 ということはよく聞くのですが，なぜ，等速度運動する荷電粒子は電磁波を出さないのかが分からないのです．

荷電粒子（以後粒子と書きます）と共に動く慣性系から見れば，粒子は静止したままだから，電磁波を出しそうにはありません．しかし，等速度運動をしているということは，空間の電場が変化するから，その結果として磁場が生じ，さらにその結果電場が生じ…という具合で，電磁波が出されそうにも思えます．電磁波が出されれば，粒子は運動エネルギーを失うから，いずれ静止してしまうことになる．でも，それだと明らかに，荷電粒子と共に動く慣性系から見た場合とは矛盾してしまいます．

いったい，この議論はどこが間違っているのでしょうか．よろしくお願いします．

arc さんのレス (2005/01/28(Fri) 17:36)

すみません，自己紹介が抜けていました． 僕は大学一年生で，電磁気学を学んだばかりの者です． 初等的な質問かもしれませんが，よろしくお願いします．

おこめ さんのレス (2005/01/28(Fri) 18:44)

arcさん，はじめまして．まず言葉で言わずに数式で矛盾を示してみてください． それが示されない場合，なぜ矛盾だと感じるのかを教えてください．

arc さんのレス (2005/01/28(Fri) 19:30)

いくつかの教科書を見てみて，荷電粒子の電磁波の放射に関するところを読んだりしたのですが，確かに出てくる結果は，荷電粒子の加速度がゼロであれば，電場，磁場がゼロになり，電磁波は出されていないことになるようですが，僕が読んだ教科書では，荷電粒子から十分遠方で議論していて，近くではどうなっているのかが分からないのです．

十分遠方で電場や磁場がゼロであれば，つまりは電磁波が来ていないというわけだから，電磁波は発生していないということになると思うのですが，それでは，荷電粒子の近くの電場や磁場の変動はどうなったのかが分からないのです．

電場が変動すれば，

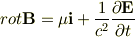
及び，

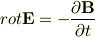
から，電場が変動＞そのまわりの磁場が変動＞そのまわりの電場が変動… と続いていって，電磁波が発生しそうな気もするのです． でも，そうはなりませんよね…． とりあえず，荷電粒子が動いている場合，電場が変化するのは間違いないと思うのですが…． また，仮に電場が変動して，磁場も生じたとしても，Poynting Vectorがゼロになれば電磁波は出ていないことになるのかな？などとも考えたのですが，やはりよく分かりません．

最初に矛盾といったのは，上の文章のとおりで，数式では矛盾しないと思うのですが，なぜそうなるのかが直感的によく分からないんです．数式を用いずに，直感的に考えたら，上のような矛盾めいた結論になってしまう…．これは数式の方が正しいんだと思って勉強を進めることもできると思うのですが，なんだかモヤモヤしたものが残って気持ちが悪いんです．

おこめ さんのレス (2005/01/28(Fri) 19:45)

分かっているとは思いますが，マクスェル方程式はガリレイ変換に従いませんよ． そこが直感とずれるところではないですか？後，荷電粒子の運動を考えているのであれば，粒子の運動方程式を考えてみてください．

それから関数の変数を書かないのが原因でどこから見ているのか分かってないのではとも思います．よくxを観察する場所，x'を電荷の位置として区別します．

arc さんのレス (2005/01/28(Fri) 20:20)

早い回答，ありがとうございます． マックスウェル方程式がガリレイ変換に従わない，というのは，お話程度に聞いたことがあるくらいです．そこから特殊相対論が生まれた？基本であるMaxwell方程式に光速cが入っているということは，ガリレイ変換に対して，不変ではない．そういう話だった気がします．

荷電粒子の運動方程式は

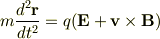
でしょうか．（ただし，上の式のローレンツ力は自己力によるもの） 等速度運動をする場合は右辺がゼロになる？と考えれば，確かに，等速度運動を続けるから，電磁波も発生しそうにないのですが…．

ガリレイ変換すると，電場や磁場はどのように変わるのでしょうか．それでも，やはり，電場が変化して，その結果磁場が変化して，というようなことが起こりそうな気がするのですが…．電場や磁場が変化しても電磁波を出さないということはあるのでしょうか．

おこめ さんのレス (2005/01/28(Fri) 20:33)

簡単のために電磁波がある一定の方向を向いて進行している場合を考えてます．

電磁波は真空では磁場成分と電場成分は直交（divE=0,divB=0）しています．運動方程式の左辺がゼロなのでｑ≠０，磁束密度，電場が荷電粒子の進行方向に直交する．ｚ軸を荷電粒子の進行方向にとってみるとx,yに電磁場が振動しています．しかしその成分はゼロなので電磁場を変化させない．これでよろしいでしょうか？

ほんとは荷電粒子は電気分極します．つまり電磁波の発生の一番簡単な例は変動する電気双極子を考えることです．

僕も詳しくやってないので間違いがあるかもしれません．なので後で調べてみてください．それから電磁気学は変動しない場で基礎はほぼ全て完成してしまうので，そこから見直したほうが近道かもしれませんね．

EMAN さんのレス (2005/01/28(Fri) 21:30)

> それでも，やはり，電場が変化して，その結果磁場が変化して，というようなことが起こりそうな気がするのですが…．電場や磁場が変化しても電磁波を出さないということはあるのでしょうか．

arcさん，こんばんは．

電場と磁場が変化しても，電磁波にならない形はありますよ．

電荷の周りには電場があります． 静止している人には電場にしか見えません．

ところが静止電荷に対して運動している人から見ると， そこには磁場も見えます． 電荷についてはあまり考えずに，ただ電磁場に注目した方がいいです． 電場をローレンツ変換してみると答えが出ます．

多分，思いもよらない結果になると思います． 私はこれを知った時，とても感動しました．

ＥＭＡＮ さんのレス (2005/01/29(Sat) 00:08)

電場をローレンツ変換する，と書きましたが，難しいかと思います．

この話題については一年ほど前，某掲示板で議論されました． 大変懐かしく思います．

以下はその時の議論のまとめ（試作）です．

• http://homepage2.nifty.com/eman/bbs/elemag/jiba.html

良ければ参考にしてみて下さい．

arc さんのレス (2005/01/29(Sat) 02:03)

ローレンツ変換って，名前は聞いたことはあるけれど，どういうものか知らなかったので，ちょっと調べて，とりあえず計算してみました． 計算は，Maxwell方程式を使ってやってみました．すると，静止電荷に対して運動している方向の成分は変化せず，垂直な成分には磁場が出てくることが分かりました！磁場の計算はしていないのですが，この調子だと，運動に平行な成分は変わらず，垂直な成分には電場が出てきそうです．

これはつまり，動いている系で見たら，静止している系での電場のいくらかが磁場になって見えたり，磁場が電場になって見えたりするということでしょうか． これは面白い結果です．

ところで，静止電荷を運動している人から見ると，静止している人とは電場や磁場が違って見えるということが分かりましたが，電荷が動くわけだから，運動している人から見ると，電場と磁場が平行移動しているような感じになりますよね？そうすると，これは，EMANさんがおっしゃった「電場と磁場が変化しても，電磁波にならない形はありますよ」という一つの例なのでしょうか？

arc さんのレス (2005/01/29(Sat) 02:36)

掲示板，見ました．とても参考になりました． つまり，電場の変化と磁場の変化の連鎖が起こらない，ということですね？ ただ，きちんとMaxwell方程式は満たしていると．ちょっと特殊な例を考えてみたりすると，確かにそんな気もしてきました．

では，電磁波を出すときと出さないときでは何が違うんでしょう？Poynting Vectorを計算するしか，それを判別する手段はないでしょうか？質問攻めですみません．

やかん さんのレス (2005/01/29(Sat) 15:04)

arcさん，はじめまして．私はMaxwellの方程式理解しきってないのでここのスレでレス書いていいものかどうかちょっと躊躇したのですが，もしかしてＥとかＢの時間微分がゼロだとだめ，つまり，電荷の等速度運動のような，定常電流では，時間微分がゼロですから，電磁誘導がおきないんじゃないんでしょうか．（ラジオに”ジッ”と雑音が入るのはスイッチを入れたときだけ） ポインティングベクトルは，ＥＸＨだから時間微分がゼロでも定義できるのでは． ポイントずれてたらすみません．

おこめ さんのレス (2005/01/29(Sat) 16:20)

＞ポインティングベクトルは，ＥＸＨだから時間微分がゼロでも定義できるのでは．

変動しない場ではE×H＝０です．静電場，静磁場とわけて考えることができるのは電場と磁場がいつも変動しない場では線形独立だからだと思います．

やかん さんのレス (2005/01/29(Sat) 19:11)

>変動しない場ではE×H＝０です．

あっ，そうなのですか・・．ポインティングベクトルは電気エネルギーを運んでいるのだと思ってました．また私間違ったこと書いちゃってすみません． おこめさん有難うございます．

おこめ さんのレス (2005/01/29(Sat) 19:54)

間違ったかもしれません．次のような計算をしてみました．

荷電粒子の運動エネルギーTの変動を計算すると dT/dt=v(t)・f(t)=v(t)・q(E(r(t))+v(t)×B(r(t))=qv(t)・E(r(t)) q(x)v(x)=j(x)=j(x')δ(x'-r(t)) =∇×H j(x)・E(x)=(∇×H)・E=-∇・(E×H)+H・(∇×E)=-∇・S ∫j(x)・E(x)dV=-∫S(r(t))ndS d/dtT=∫j・EdV=-∫SndS です． 場だけに注目すると d/dtE(total)=d/dt[E(e.m.)+E(mech)]=d/dtE(mech)=j・E=-∇・S だから電磁場のエネルギー時間変化はゼロですが，全エネルギーの時間的な減少量は表面から流れ出るエネルギー流密度ポインティングベクトルに等しいことが分かります．これがゼロになるということはオームの法則E＝σjのσ=0 or j=0の場合だけということになります．だから自分の以前の発言はすごい特殊な（理想的な）場合を言っていたようです．ごめんなさい．

Dr.StrangeLab さんのレス (2005/01/30(Sun) 15:56)

出張している間（ボストン雪降りすぎ！）に面白そうな議論が終わっている… んで，ふと思ったのですが． ・導線に一定の電流が流れるとき，電子は電場で加速→金属原子に当たって停止 を繰り返しているわけですが，この金属原子に当たるときに制動放射は出ないのでしょうか？ （微弱過ぎて検出できない？）

arc さんのレス (2005/01/31(Mon) 09:09)

皆さん，ありがとうございました．とても参考になりました．これからも有益な議論を眺めさせてもらいます（笑）場合によっては書き込みます．

＞Dr.StrangeLabさん

確かに，それだとなんか出てきそうですよね…．

やかん さんのレス (2005/01/31(Mon) 12:54)

＞おこめさん ＞荷電粒子の運動エネルギーTの変動を計算すると，

おおっ，うー，難しい・・．なんか自分が何にもわかってないで書き込んでるのが 良くわかりました．やっぱ，こういう風に数式がすらすら計算できる上で じゃないと駄目ですよね ・・． (^^;

Dr.StrangeLabさん >出張している間（ボストン雪降りすぎ！）に

海外出張に行ってらしたんですね．お帰りなさい〜いヽ(´▽｀)/

＞導線に一定の電流が流れるとき，電子は電場で加速→金属原子に当たって停止 を繰り返しているわけですが，この金属原子に当たるときに制動放射は出ないのでしょうか？

これって，やっぱり出てるんじゃないかなー．きっとおっしゃるように ＞微弱過ぎて検出できない？ のような気が私もします・・．

CO さんのレス (2005/01/31(Mon) 14:04)

>・導線に一定の電流が流れるとき，電子は電場で加速→金属原子に当たって停止 >を繰り返しているわけですが，この金属原子に当たるときに制動放射は出ないのでしょうか？

交流電流の流れている電線なんかも怪しいですよね (^^;

やかん さんのレス (2005/01/31(Mon) 18:42)

COさん，こんにちは．

＞交流電流の流れている電線なんかも怪しいですよね

あっ，なんかいっぱい出てそう・・．なんとなくそばよると体に悪そうですね (^^;

かつ さんのレス (2005/01/31(Mon) 21:41)

みなさん，こんばんは．

> ボストン雪降りすぎ！

私も実は先週，木曜までドイツ（バイエルン地方）でしたが，さらっさらの パウダースノーが毎日降ってました :)

> 交流電流の流れている電線なんかも怪しいですよね (^^;

定量的に何かあれば面白いですねぇ．例えば，電線の抵抗と空間のインピーダンス の関係とか，抵抗率と長さと線幅と周波数で決まる関係とか・・・

やかん さんのレス (2005/02/01(Tue) 12:14)

かつさん，こんにちは．

＞私も実は先週，木曜までドイツ（バイエルン地方）でしたが，さらっさらの パウダースノーが毎日降ってました

あっ，いいなあ．もしかしてスキーとかやられました？ :)

そういえば”電流から電磁波，交流”で思いだしたのですが，昨シーズンスキーに行ったとき，ゲレンデの鉄塔に高圧線らしきものが走っていて，リフトで上っているときに， 電線が”ウィ〜ン”ってうなってるんですよ．どう考えてもリフトの振動と関係なさそうだし，高電圧だろうから，空中に放電してるのかな，なんて勝手に解釈していたのですが，翌日は不思議と音はしませんでした．あれってコロナ放電とかいうやつかな．暗くなかったから何も見えなかったけど，きっと湿度によっても放電量とか違うんでしょうかね．でもそうすると空中放電は，電磁波放出と別におきてるんでしょうか．

かつ さんのレス (2005/02/01(Tue) 22:15)

やかんさん，こんばんは．

> あっ，いいなあ．もしかしてスキーとかやられました？

いえ，私はスキーはやりません．ま，それ以前に仕事で行ってますし (^^;

> 電線が”ウィ〜ン”ってうなってるんですよ

会社の近くに東京電力の変電所があって，うなっていますけど，あれは そもそも，電線がうなっているのですかね？ もしかして変圧器が磁歪でうなっているのか？とか考えてましたが・・・ 定かな理由は解りません (^^;

やかん さんのレス (2005/02/02(Wed) 20:15)

>いえ，私はスキーはやりません．ま，それ以前に仕事で行ってますし

あっ，お仕事だったのにすいません，失礼な事言ってしまいまして．つい，自分の感覚で考えてしまいました (^^;

＞会社の近くに東京電力の変電所があって，うなっていますけど

あっ，そうそう，私も変電所で音聞いた事ある．でもスキー場はトランスなかったような． なんか，いかにも電磁波出てるっていう感じの音しますよね（非科学的な言い方ですみません (^^; )

おこめ さんのレス (2005/02/02(Wed) 20:58)

音が届くということは音波は出ていますね :)

かつ さんのレス (2005/02/02(Wed) 21:12)

音波が出ると言ふことは・・・電線ないしは付属物に力学的な力がかかっている． って事は・・・磁歪 または ローレンツ力．周辺に変圧器が無かったとしたら 後者しか無いんですが，それなら高圧線よりも低圧の方が電流は大きいやうな？ なんか不思議 (^^;

やかん さんのレス (2005/02/03(Thu) 17:13)

きっと交流だから，やっぱなんかが振動してるんでしょうかね :) そうすると，音の周波数も関東なら，50Ｈｚだったりして． 時報の”ポッ，ポッ，ポッ”の音が，確か音名”イ”（ハ長調のラ）４４０Ｈｚだから， 220，110，55，だから，えーっと，３オクターブ下，ぐらいかなあ・・． (^^;