エネルギー

タケオさん，はじめまして．面白い考えですね．私は大学でちゃんと物理を勉強したわけではないので，学問的に正確な議論はできないのですが，一般向けの入門書を読んだときに，”静電エネルギーは空間に蓄えられている”ような表現の記載は見かけた気がします（それが良い表現なのか，あるいは一般向けの多少不正確なぶっちゃけた比喩なのかはわかりませんが）．空間のゆがみとか，ひずみっていうのも，物理で良く聞きますよね．現実の巨視，可視的なイメージとして，なんとなくしっくりくるような気はするなあ．結局，原子レベルの微視的な物や，不可視的な物って，どう考えたって，本当に正確なイメージって，できないかもしれないから，既知の法則，事実，データに矛盾しない当座の条件で考えるなら，ゆがみ，ひずみ，ねじれ，などの言葉も使っても許されるかなあって気もしますけど（やっぱ駄目かな）

＞二乗部分がひずみであるのことが多いような気がします

そう言われてみれば，そんな気も・・．さささんのおっしゃるように２乗はエネルギー求めるときに積分するからなのでしょうが，それは抜きにしても，そのエネルギーが何のひずみ（に例えられる）か，という事ですよね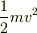． $\frac{1}{2}mv^2$ って，特殊相対論で増加した質量の一次近似分でしたっけ？えーっと，質量のゆがみ？駄目かなあ（絶対信用しちゃ駄目ですよ）．

Re: エネルギー

タケオさんのレス (2005/01/24(Mon) 19:25)

ありがとうございます．

＞特殊相対論で増加した質量の一次近似分でしたっけ？えーっと，質量のゆがみ？駄目かなあ（絶対信用しちゃ駄目ですよ）．

確かに，，，そこまで考えが及びませんでした． mc^2〜m0c^2 + 1/2 mv^2ですよね．なるほどぉ．

信用しちゃいますっ．ありがとうございました．

数学的に出た式でも，いつも意味を見出そうとしてしまうんですよね．最終的にはイメージできないような世界を物理で扱っていくのかな？ちょっと不安です．

Re: エネルギー

おこめさんのレス (2005/01/24(Mon) 22:45)

>仕事が力を距離で積分したものなら二乗が出てきて当たり前なんですが，物理的には意味がないのかなぁと思いました．

どうもはじめまして．上に書かれているのは仕事が運動エネルギー変動に等しいことを言っているのであってエネルギー一般についての話ではないと思います．仕事というものの法則は面白く，非力でも倍の量動かせば同じ結果が得られるという不思議な性質がありますね．

ところでエネルギー（正しくは全エネルギー）というものの物理的な意味は「かならず保存する量」という意味しかありません．関数がどのような顔をしていようが全エネルギーは必ず保存（時間微分がゼロということです）します．運動エネルギーは物理量の２乗に比例すると思いますが，クーロンポテンシャルなどのポテンシャルエネルギーは一般にそんなことはいえないと思いますが，そこのところはどうお考えでしょうか？

それからエネルギーが保存しなければ，どこかエネルギーを数え忘れているということです．ただし，現在の量子力学では不確定性原理の範囲でエネルギー保存則は破れてしまう（物理量がゆらぐ）そうです．本題からずれてしまったようですが，これに対する意見や誤りの訂正をお願いします．

Re: エネルギー

やかんさんのレス (2005/01/25(Tue) 13:12)

＞信用しちゃいますっ．ありがとうございました．

あっ，デタラメだから駄目ですってば (^^;

>数学的に出た式でも，いつも意味を見出そうとしてしまうんですよね．

私偉そうな事言える学力ないのですが，これってものすごく大切な事のような気がします．私は幼稚な例しかあげられないのですが， A（払った金額）−B（商品の値段）＝C（おつり）という，公式があったとして 600円の商品に500円払ったら，この公式が使えると仮定して 500-600=-100 答えマイナス100円のおつり！って数学的にはなります．代表的なマイナスの解釈には確か３つぐらいあって（意味が逆，基準値（ゼロ）以下，解不適，だったかな），この場合は，逆の意味，おつりはゼロで，100円追加で払う，と人間が解釈しないと，意味が通じません．（あるいは，A<Bの際はこの公式は使えない，とするか．）こんな問題の解釈はみんな頭で瞬時にやってますが，もっと複雑な事象を扱う方程式で複素数なんかが出てくると，数式や，特に解がちゃんと意味を持つかどうかという事を考えるのはきっととても大切なんでしょうね．

＞最終的にはイメージできないような世界を物理で扱っていくのかな？ちょっと不安です．

電子を丸で書いたり，原子核をツブツブで書いたり，ブラックホールをアリジゴクみたいに書いてるの見ますけど，もちろん，正確じゃないでしょうし・・．でも不正確ながらイメージしないと駄目なんでしょうね．世界地図で，なんとか図法とか，ありますけど，定点からの距離はあってるけど，面積違うとか，地球儀以外正確ではないと言ってしまえばそれまでですが，その都度，利用，応用できれば不正確もありかな，なんて思ったりもします．わかってないのに生意気ですみません．

Re: エネルギー

おこめさんのレス (2005/01/25(Tue) 17:40)

＞最終的にはイメージできないような世界を物理で扱っていくのかな？ちょっと不安です．

物理学一般(他の分野でも同じだと思いますが)に言えますが，イメージを作るために２次元グラフでよく展開します．運動状態を知るためには運動量と位置の座標で展開することで評価することができるます．他にもエネルギーと位置，時間など好きなように２次元に貼り付けて現象を説明していきます．どれだけ多次元でも，二つの要素の相互関係を見るのに２次元のグラフを使うのが一番効果を発揮できて，これはちょうど解析力学の位相空間の項などで説明されています．

またこの手法は量子力学でも使えて，ディラックのブラベクトル，ケットベクトルなどといって，一般に状態を|a>などとあらわして，これを好きな変数で展開するといったようなことをします．たとえば状態|φ>のxとの関係を知りたければ内積をとることによって<x||φ>＝φ(x)とできてφという得体の知れないものをｘで表すことができます．他にも粒子数（エネルギー）で展開することも多いですね．（粒子数の張る空間をフォック空間と言うんでしたっけ？）ともかく全てを同時に知ることはできなくても知りたい二つの関係を知ることはできるということです．

量子力学なんかじゃなくて例えば人も同じです．たとえば「A君はB君に親切だ．」という観測が得られたとしても，新しく「A君はC君には不親切だ」という事実が得られるかもしれません．これは親切，不親切だというひとつのものさしで話をしましたが，A君は男だ，とかA君は学生だ，A君は３１歳だとかいって，パラメータは無限次元に「A君という状態」を作ることができます．互いの状態をそれぞれの軸にとって展開することで状態の相互関係が分かると言った感じです．更にどんな風に親切だとか修飾していく様な感じで強い力とか弱い力などを入れるのが場の量子論ですね．

間違っているかもしれませんが僕はこんな感じで物理をイメージ付けてます．

Re: エネルギー

タケオさんのレス (2005/01/26(Wed) 00:04)

おこめさん，やかんさんありがとうございます．

量子力学は数学的にしか理解できないものなのかと思ってました．多次元のものでも二次元の関係は見ることができるんですね．全くイメージとかけ離れていくわけではなさそうでよかったです．

>>仕事が力を距離で積分したものなら二乗が出てきて当たり前なんですが，物理的には意味がないのかなぁと思いました．どうもはじめまして．上に書かれているのは仕事が運動エネルギー変動に等しいことを言っているのであってエネルギー一般についての話ではないと思います．

おっしゃるとおりですね．すいません，自分でも何が言いたかったのか，，．

>運動エネルギーは物理量の２乗に比例すると思いますが，クーロンポテンシャルなどのポテンシャルエネルギーは一般にそんなことはいえないと思いますが，そこのところはどうお考えでしょうか？

ポテンシャルエネルギーは特別なものなんじゃないかなと思ってました．保存力だからポテンシャルが定義できるわけで，他のエネルギーとは少し異質で，つじつまあわせ？ではないですが，たまたまきれいな（二乗ではない）形になっているだけかと．んん，よくわかんないです．

Re: エネルギー

おこめさんのレス (2005/01/26(Wed) 16:06)

関数形の形を見て運動に関するエネルギー次元を持つ量が速度の２乗に比例する．ということをニュートン力学が予言し，それが実験と近似的に等しい結果を示しているということしか分からないということでは駄目ですか？

他のエネルギーについてもそうです．エネルギーという概念自体が物理学で最も抽象的な概念のひとつで，エネルギーがいつでも変化しない事（これがエネルギーの哲学的，または主観性を排除した定義）からそれを見るだけでどんな運動かが理解できるという風にも言えます．

物理で，どんな運動かを理解するときに運動方程式を見る方法とグラフを見る方法などがあります．でも一番コンパクトなのが方程式で，最も正確な内容を含んでいます．だから最終的に実験から得られた情報を方程式にまとめていつでも使えるようにするんです．そこから更に方程式をいろんな形に変形してその方程式の性格を知ったり，実験していないような内容でもシュミュレーションすることができるってことですね．その結果エネルギーや，運動量などというものさしを利用して現象を評価しようって事でしょうね．エントロピーなんかもそんなものに含まれます．

エントロピーで思い出しましたが，熱力学の関数なんかが丁度良い例ですね．あれは実際にどんな常態なのか全ては分からないわけですが，熱については熱力学関数で知ることができます．熱力学関数には色々名前がありますが，一つの状態を色々な変数で展開した結果に過ぎません．とりわけ化学などの分野ででギブズの自由エネルギーとよばれる関数がもてはやされるのは実験系の状態によくなじむというだけです．

[home] [掲示板] [ページの先頭]