雪＠物理初心者 さんの書込 (2005/01/20(Thu) 13:44)

はじめまして．物理初心者の雪です． 大学で一応物理をかじってますが…物理，難しいです…．

量子力学の授業で， 「エルミートの多項式，ルジャンドルの多項式，ラゲールの陪多項式のそれぞれの意味と，どういう場面で使うべきなのかを調べよ．」 という課題が出たんですが…． 普通に計算問題なら何となく分かるのですが， 意味を改めて聞かれると分からなくなってしまいました． 意味って言うと…普通の式だけでは説明が足りないのでしょうか…．

どなたかご教授お願い致します．

Joh さんのレス (2005/01/20(Thu) 20:17)

雪さん，はじめまして．

私は，量子力学のことは良く知りません．具体的にどういう場面で役に立つのか，きっと他の人が教えてくれるでしょう．

それぞれの数式の意味ですが，どれも超幾何関数という，超幾何方程式の正準形の解の一つとして表現されるものです．超幾何方程式の正準形というのは というような微分方程式で，0,1, 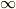で特異点を持ちます．例えば，ルジャンドル多項式はa=-n, b=n+1,c=1,x= 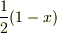とした超幾何関数です．ラゲール多項式やエルミート多項式は，超幾何方程式の特異点を0と 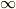だけにまとめてさらに簡単にしたものの解で，合流型超幾何関数というものです．数学的に言うとどれも超幾何関数の一種で，乱暴に言えば同じようなものです．

物理的な意味ですが，これらの関数を使うと微分方程式が変数分離型に出来るので便利だということが言えるでしょう．例えばルジャンドル多項式を使うと，球面ラプラス方程式が変数分離型に出来ます．

あんまり，期待されていたような回答にはなっていないかも知れませんね．特に分からないこととか，雪さんなりに考えたことなんかを書いていただけるといいんですが．

おこめ さんのレス (2005/01/20(Thu) 22:23)

半年ほど前に僕が教授に質問した内容と同じです．教授はたいした意味は無いと言ってました．要するにシュレーディンガー方程式にポテンシャル関数を代入してやって級数展開法で解いてやったときに出てくる解がそれらの関数であるというだけです．ルジャンドル関数なんかはたしか電気双極子モーメントの解だったと思うので古典的対応を考えるときに便利というだけです．僕自身も今はたいした意味は無いと認識しています．