無題

物理苦手ですさんの書込 (2005/01/19(Wed) 18:19)

「半径ｒの円盤が滑らかな水平面上で中心の周りに角速度ｗで回転しているとき，ヘリ上の一点を固定した．固定点の周りには自由に回転できるものとするとその回転の速度はどれほどか？」という角速度保存の問題が出たんですが，よくわかりません．誰か教えてくれませんか？

ヘリ上と円盤の関係が，この問題文だけでは読み取れません．

ここで言う角速度保存とは，フィギュアスケートで手を引っ込めると（半径を小さくすると）角速度が増す，というやつでしょうか．

ちょっと甘いかと思ったのですが，

> ヘリ上と円盤の関係が，この問題文だけでは読み取れません．

と言うのが気になったもので，釣られてきました．（笑数式打ち込みの練習も兼ねて書き込ませて頂きます．

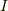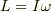この円盤の重心周りの慣性モーメントをとすると，角運動量は， $L=I\omega$ と表せます．

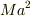ここで縁を押さえると，回転の中心は重心から半径だけずれた位置になるので，円盤の質量をとすると慣性モーメントは Ma^2 だけ増えます．（平衡軸の定理）

後は角運動量保存を使って求められるでしょう．

EMANさんありがとうございます．ヘリっていうのは，ヘリコプターのことではなかったんですね．切腹…．

> ヘリっていうのは，ヘリコプターのことではなかったんですね．

え？！

誤字がありました．「平衡軸」じゃなくて「平行軸」です．物理苦手ですさん，間違って覚えないように気をつけて下さい．