大学のレポートで・・・

ナックルさんの書込 (2005/01/19(Wed) 17:26)

２次元の運動を考える．慣性系でｘ方向に速度ｖで等速に運動している質量ｍの物体Ａを等角速度ωで回転している座標系から見たときを考える．ただし，ｔ＝０で，Ａは原点におり，そのとき２つの座標は重なっているとする．回転している座標系での運動方程式を解いて，回転している座標系での物体の位置と速度を求めよ．

という問題なんですが，よくわかりません．どなたか教えてくれませんか？

どこが良く分かりませんか？

まずは

> 回転している座標系での運動方程式

これをたててみて下さい．

おそらく・・・

md^2X/dt^2 = 2mωdY/dt + mω^2X

md^2Y/dt^2 = -2mωdX/dt + mω^2Y

だと思います．

お願いします．

おそらく

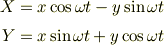
$X & = x \cos \omega t - y \sin \omega t\\Y & = x \sin \omega t + y \cos \omega t$

を微分したのだと思いますが，そうすると 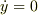$\dot{y} = 0$ の条件を使って

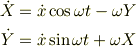
$\dot{X} & = \dot{x} \cos \omega t - \omega Y\\\dot{Y} & = \dot{x} \sin \omega t + \omega X$

となります．ここで 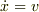$\dot{x} = v$ の条件を使い忘れていませんか？これをつかったのちに，さらに微分して整理すると

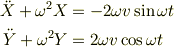
$\ddot{X} + \omega^2 X & = - 2 \omega v \sin \omega t\\\ddot{Y} + \omega^2 Y & = 2 \omega v \cos \omega t$

となります．この微分方程式は・・解けそうな形ですよね．