誰かお願いします．

home > 掲示板 >

このページのPDF版

サイトマップ

誰かお願いします．

かきっこさんの書込 (2005/01/19(Wed) 15:43)

e＾ｘ/x の積分の仕方をおしえてください．

物理科の学部１年生です．テストでこまってます．すいませんが誰か教えてください．

Re: 誰かお願いします．

やかんさんのレス (2005/01/19(Wed) 16:35)

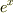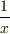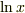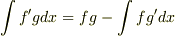かきっこさん，こんにちは．私の学力ではお教えするなどということはできないのですが確か e^x って，何回微分しても積分しても形が変わらないんでしたっけ？ $\frac{1}{x}$ は，積分すると， $\ln x$ それと， $\int f'g dx= fg - \int fg' dx$ っていう公式ありましたっけ？ fとg,どっちかにどっちか入れると，できそうですね．ちょっとやってみていただけますか？違ってたらすみません．

Re: 誰かお願いします．

CO さんのレス (2005/01/19(Wed) 18:17)

やかんさんの方法でうまくいくかな..？

この問題，どこから持ってきましたか？(正しいですか？ (--;)

Re: 誰かお願いします．

やかんさんのレス (2005/01/19(Wed) 18:41)

COさん，こんにちは．いつもお世話になります．

＞やかんさんの方法でうまくいくかな..？

す，すいません・・．自分でもやってみたのですがあれえ，うまく行かない・・．ちょっと甘かったです．これからはちゃんと自分でといてからレス書くようにします（反省！）かきっこさん，間違ってごめんなさいm(__)m

Re: 誰かお願いします．

おこめさんのレス (2005/01/19(Wed) 20:07)

級数展開法でできるのではないですか？ e^x=?n=0,∞(1/n!)x^nですから(e^x)/xは容易に積分できると思います．実関数で積分しづらいときは複素数積分でやるのが良いらしいです．しかしこの場合はどうなのでしょう？

Re: 誰かお願いします．

CO さんのレス (2005/01/19(Wed) 21:11)

> 級数展開法でできるのではないですか？ > e^x=?n=0,∞(1/n!)x^nですから(e^x)/xは容易に積分できると思います．

やるとどうなります？解析解がでてきますか？

Re: 誰かお願いします．

おこめさんのレス (2005/01/19(Wed) 22:59)

手段だけ示しただけで，まだ計算していません．初等関数の級数展開に積分値がならなければ多項式でしか定義できないのではないですか？あきらかにx=0で発散するので級数展開法ではなく複素積分が妥当かもしれませんね．いずれにしても計算はしていないです．

Re: 誰かお願いします．

山本明さんのレス (2005/01/22(Sat) 16:59)

数式打ちの練習がてら．おこめさんの記述そのままですけど．

手元の数学公式集には，

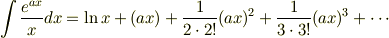
$\int \frac{e^{ax}}{x} dx= \ln x + (ax) + \frac{1}{2\cdot 2!}(ax)^2 + \frac{1}{3\cdot 3!}(ax)^3 + \cdots$

と書いてありますね．これは級数展開をしてますね．

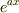$e^{ax}$ をテイラー展開をすると，

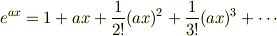
$e^{ax}= 1+ax+\frac{1}{2!}(ax)^2+\frac{1}{3!}(ax)^3+\cdots$

なので，

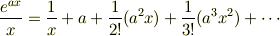
$\frac{e^{ax}}{x}&= \frac{1}{x}+a+\frac{1}{2!}(a^2x)+\frac{1}{3!}(a^3x^2)+\cdots$

です．これを積分すれば，

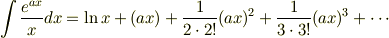
$\int \frac{e^{ax}}{x} dx= \ln x + (ax) + \frac{1}{2\cdot 2!}(ax)^2 + \frac{1}{3\cdot 3!}(ax)^3 + \cdots$

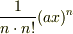となるでしょう．この先 $\cdots$ の部分は似たような形の項になり，を使って表せば $\frac{1}{n\cdot n!}(ax)^n$ で，は無限大までの和となります．

積分領域によっては，複素積分を導入した方がやさしいかもしれませんが，不定積分ではこれが限度だと思います．（うわー，数式掲示板って気持ちいいなぁ！COさんお疲れさまでした!!）

Re: 誰かお願いします．

CO さんのレス (2005/01/22(Sat) 17:14)

なるほど．これでも「解けた」と言うんですね．大学一年生の質問なので，解析解(というかきれいな解)を期待しているのだと思いました．なので私は「問題を写し間違えているのでは?」と疑ってます．(^^; # 質問者の方，問題があっているか教えて下さい．もう見てないかな :(

> うわー，数式掲示板って気持ちいいなぁ！COさんお疲れさまでした!!

ちょっと面倒かもしれないけど，やっぱり数式は数式として書きたいですよね :)

Re: 誰かお願いします．

Joh さんのレス (2005/01/22(Sat) 18:05)

ご質問の積分は，積分指数と呼ばれるもので，次のように普通表記します．

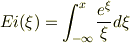
$Ei(\xi)=\int _{-\infty }^{x}{e^{\xi }\over \xi }d\xi$

解析解は出ません．

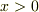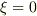領域 x>0 において， $\xi=0$ で発散してしまいます．ご質問は不定積分のようになっていましたけど，どういう答えが求められているんでしょうか．広義積分の主値ということでしょうか．級数展開は山本さんの書かれたもので合っていると思います．(定数が要るかも．)

いずれにしても難しい問題ですね．

Re: 誰かお願いします．

やかんさんのレス (2005/01/24(Mon) 17:48)

いやあ，難しい問題だったんですね．なんか，２５手詰の詰め将棋を３手詰と勘違いしてさしちゃった気分です．（かきっこさん，すみませんでした）答えは単項式か２，３項式（解析解って言うんでしょうか）かと思っていたのですが無限級数の和になるんですね．勉強になりました．有難うございました．

Re: 誰かお願いします．

おこめさんのレス (2005/01/24(Mon) 23:53)

＞いやあ，難しい問題だったんですね．なんか，２５手詰の詰め将棋を３手詰と勘違いしてさしちゃった気分です．

解の検討がつかないときには級数展開法が広く応用できることは一回生の講義でもやることですし，機械的な作業なので求積法，定数変化法，変数分離法，逆演算子法，複素積分，フーリエ変換，ラプラス変換などの他の方法よりもやさしいと思いますよ．ただ，解が出た後に初等関数に直せるかどうか考えるとなると面倒かもしれませんね．

Re: 誰かお願いします．

山本明さんのレス (2005/01/25(Tue) 01:45)

>なんか，２５手詰の詰め将棋を３手詰と勘違いしてさしちゃった気分です．

ご安心を！私もパッと見で，やかんさんと同じこと考えました♪ その次に考えたことは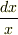， $\frac{dx}{x}$ を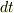にできないか？という検討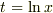． $t=\ln x$ と変数変換しようとしてみて，実際に計算してダメだと判断しました．まあ，誰だって短い手数で詰めようとしますよねっ！ (^^;

＞Johさん

勉強になりました．ありがとうございます．

Re: 誰かお願いします．

おこめさんのレス (2005/01/25(Tue) 08:32)

山本さん＞まあ，誰だって短い手数で詰めようとしますよねっ！そうですね．

ただ僕は，全く解の形が分からなかったり，積分可能かも分からないときは微分積分学によって確立された判定法などに従って手の出るところから詰めていくか，ともかく解をいろいろ代入してみるとかして，とりあえず解を見つけてからできるだけ短い手数で詰めることを考える方法が楽な方法じゃないかなぁーと思います．才能の無い僕としては機械的な手法に頼りたいところです．

Re: 誰かお願いします．

やかんさんのレス (2005/01/25(Tue) 12:21)

＞おこめさん＞解の検討がつかないときには級数展開法が広く応用できることは一回生の講義でもやることですし，機械的な作業なので求積法，定数変化法，変数分離法，逆演算子法，複素積分，フーリエ変換，ラプラス変換などの他の方法よりもやさしいと思いますよ．

うわあ，やっぱり，大学の内容はすごい．私も理学部憧れてましたが，もし入れていたとしても，ついていけなかったかもなあ (^^; ところで，この問題では結論は無理という事ですが，初等関数に直せる問題では，やはり既知の級数展開式から逆に自分で類推して，という事になりますか．当たり前のことだったらすみません・・．

＞山本明さん >ご安心を！私もパッと見で，やかんさんと同じこと考えました♪

ああ，お蔭様でなんか精神的に救われた気がします！もし，街頭とかで”この問題解けたら景品差し上げまーす”なんてやってたら，私うっかりやっちゃいそうです (^^;

Re: 誰かお願いします．

おこめさんのレス (2005/01/25(Tue) 17:10)

＞やかんさん >ところで，この問題では結論は無理という事ですが，初等関数に直せる問題では，やはり既知の級数展開式から逆に自分で類推して，という事になりますか．当たり前のことだったらすみません・・．

初等関数は 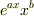$e^{ax}x^{b}$ ＝ｘ＾（b）Σk=0,k=∞｛a^(k)ｘ^(k)/k!｝でまとめることができると思います．（a∈C,b∈C）この公式を元に級数展開の解から初等関数に逆変換できると思います．一番簡単なのはやはりa=1,b=0のe^xで，ｘで微分しても無限級数の形は変わりません．上の初等関数のべき級数のm,nを好きなように変えて得られた級数解を再現できたらその初等関数が解だということになりますね．

最後に念のために，cos(ax),sin(ax),sinh(x),cosh(x)などもe^(cx)の組み合わせで作れるということを言っておきます．

Re: 誰かお願いします．

やかんさんのレス (2005/01/25(Tue) 20:23)

おこめさん，有難うございます．とても勉強になりました．m(__)m

Re: 誰かお願いします．

かつさんのレス (2005/01/28(Fri) 00:37)

亀レスでナンですが，結局 Coさんが > なので私は「問題を写し間違えているのでは?」と疑ってます．(^^; と仰っていたのは，ぶっちゃけ，虚数単位が指数に入ったフーリエ変換型のが正しい設問だったんじゃ無いかい，と言うことですか？

Re: 誰かお願いします．

CO さんのレス (2005/01/28(Fri) 04:09)

かつさん，こん＊は．

たしかにフーリエ変換型 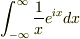$\int_{-\infty}^{\infty}\frac{1}{x}e^{ix} dx$ だと複素積分できますね． :)

>> なので私は「問題を写し間違えているのでは?」と疑ってます．(^^; > ぶっちゃけ，虚数単位が指数に入ったフーリエ変換型のが正しい設問だったんじゃ無いかい，と言うことですか？

正直に言えば元の問題までは考えていませんでした．

・学部一年生への問題である (きれいな解が出るはず) ・(学部一年の)物理で使う式にみえない・数値的にしか解けなさそう・積分区間が書かれていない

と直感から，

(こんな問題が出る可能性) << (かきっこさんの勘違いの可能性)

だと思ったので，上のように発言しました．さらに言えば，Mathematica でも解けなかったから・・ (^^;

P.S. 質問したら，見に帰ってきてほしいですよね・・・ :( こっちは議論が続いたからまだ良かったですが http://qrl.jp/?164364 (No.3864の書込)とかはかなりしょんぼりです．

Re: 誰かお願いします．

かつさんのレス (2005/01/29(Sat) 00:02)

CO さん，こんばんは．

> ・(学部一年の)物理で使う式にみえない

私もそう思いました (^^; あの形，昔，楕円関数だったかな？（最早昔の事で定かで無い (^^;）を勉強した時に偶然に出てきた記憶があって，学部一年ですごいな，なんて思いました :)

> P.S. 質問したら，見に帰ってきてほしいですよね・・・ :(

いや，全く．最近，ずっとこの傾向ですね．ちょっと萎えてしまいます．

[home] [掲示板] [ページの先頭]