チャパ さんの書込 (2005/01/16(Sun) 13:53)

ビオ・サバールの法則の導き方が分かりません．どのようにしてこのような形になったんですか？導き方の書いているページでも良いです，教えてください．

おこめ さんのレス (2005/01/16(Sun) 18:37)

マクスウェル方程式に定常電流の条件（∇・j=0,∇×Ｅ=0）を加えてやると電流に対するポアッソン方程式を得るので，それをフーリエ級数を用いて解けばベクトルポテンシャルの解がでてきます．（正しい磁場を与える範囲でベクトルポテンシャルを決めて計算しないとポアッソン方程式は出てきません．あとまず電流密度は点電荷によるものを計算して，あとで重ね合わせてください．）ポテンシャルの外積が磁束密度なので，この磁束密度の形がビオ・サバールの法則の形になっている事が確認できますよ．もしかしたら，この公式を求めるのに∇×Ｅ=0の条件は要らないかもしれません．

CO さんのレス (2005/01/17(Mon) 03:55)

こん＊は．

Biot-Savart の法則は，歴史的には，実験を積み重ねて定式化されました．

おこめさんのおっしゃってることをフォローをしておくと，静磁場での方程式は

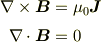
です．これに を代入すると，

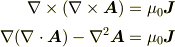
となります．ゲージとして Coulomb gauge (クーロンゲージ 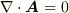)を選んでやると，

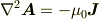
となり，おこめさんがおっしゃっている Poisson 方程式が得られます． これを適当に解いてやると(これが大変そうですが (^^; )，ベクトルポテンシャルの解が得られるということみたいです．

# おこめさんの言っていることとなにも変わりませんね (^^; # 数式を使ってみたかっただけです．(汗

やかん さんのレス (2005/01/17(Mon) 15:14)

チャパさん，おこめさん，COさん，こんにちは． えーっと，わけわかってないのにレス書くやかんです．なんか生意気っぽくてすみません． 私もからっきしわからないのでこの機会に，ごちゃごちゃお聞きしちゃおうかな，と思いました（チャパさんのスレなのにお答えでなくてすみません）．この間，こちらで御紹介いただいたブルーバックス”高校数学でわかるマックスウェル方程式”をホクホク読んでいるのですが，まずアンペールの法則 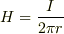は，演繹的に導いたのではなくて，測定値からアンペールが，帰納的にH（磁界）を 定義したものでしょうか？それから，以下のURLに載っていたのですが，”ビオサバールの法則”は”アンペールの法則”から導かれる（ただし高校の範囲を超える！残念！）と あるのですが，本当にそうなのでしょうか？それと，ビオサバールの法則が発表されたのは1820年10月30日，マックスウェルが生まれたのは1831年ですから，マックスウェルはそれを体系化したという事でしょうか？良くわかってないのにすみません・・． あっ，それと円形コイルの中心の磁界は 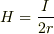と書いてあったのですが，これってこの前チャパさんが言いかけてた針のような細いものに巻くと磁界が強くなる？って，事と関連するのでしょうか？

＞ http://www.keirinkan.com/kori/kori_physics/kori_physics_2/contents/ph-2/2-bu/2-3-2.htm#Anchor-5253

チャパ さんのレス (2005/01/17(Mon) 17:06)

え〜今からチャパさんの謝罪会見を始めます．礼！ ぬおおお〜〜〜やっぱりこの分野は少し私のようなものでは早すぎたか・・・ うん読めば読むほど分からなくなってくる・・・最近回転や発散，勾配などを覚えたばっかだから・・・せっかくみなさんが教えてくれたのにすみません・・・今度またあらためて勉強します．でも，大まかには分かった気がします．

Dr.StrangeLab さんのレス (2005/01/17(Mon) 18:41)

やかんさん＞”ビオサバールの法則”は”アンペールの法則”から導かれる やかんさん＞（ただし高校の範囲を超える！残念！）と

高校の範囲を超える〜っていうじゃな〜い？ でも，高校の範囲でもなんとかなりますからぁ〜残念！ ということで下をどうぞ． （ベクトルの外積が高校の範囲外というのは聞かなかったことにします^^）

電流I[A]が流れる長さds[m]の部分を考えます． この部分から距離rの位置に磁荷qm[Wb]を置きます． 磁荷qmからr[m]離れた場所の磁束密度B[Wb/m^2]は B = qm/(4πr^2)…1)

この磁束密度Bから，電流Iの流れる長さds[m]の部分が受ける力F1[N]は F1 = Ids×B…2) 2)に1)を代入し， F1 = Ids×rqm/(4πr^3)…3)

ここで，電流Iの流れる長さds[m]の部分が作り出す磁界をdH[A/m]とすると， この磁界により磁荷qmが受ける力F2は F2 = qm・dH…4)

作用反作用の法則より，F1=F2であるので，3)及び4)から， qm・dH = Ids×rqm/(4πr^3)…5)

qmを両辺から除いて dH = Ids×r/(4πr^3)

でいかがでしょう？ （磁荷が出てきたり，微小線分の電流…どこから電荷が供給されているのか？ とか，怪しいものがいろいろ出ていますが…m( )m）

やかん さんのレス (2005/01/17(Mon) 19:32)

Dr.StrangeLabさん，一緒に乗っていただいた上，お教え頂いて有難うございます ヽ(´▽｀)/ B=μHといいますが，まず”H（磁界）”はアンペールの法則で定義したとして 磁束密度Bは，電荷のような”磁荷”というものが存在するとここで”磁荷”を定義し，比例した”磁束”というものが出ているとすると，同心球上の表面積とBはきっと反比例するから， ＞B = qm/(4πr^2)…1)

高校の教科書に出てくる，F=IBＬも実験から得られた式らしいですね．あとは，別々に出てきた，ＢとＨを透磁率μで結びつける，・・のかなあ．

＞この磁界により磁荷qmが受ける力F2は

F2 = qm・dH…4)

磁界Ｘ磁荷が，力になるんですね．これは電気のＦ＝ｑＥそっくりですが，きっと電気同様こうなる，という事で最初から定義がなされたのかなあ． Ｈはアンペールの法則で定義済み，磁荷は上のＢで定義したとすると， あれえっ，あっ，いいのかなあ・・．なんか私，なまじB=μHとか，F=IBＬとか うろ覚えしてると，どれが実験からの経験式なのか，どういう順番でどれがどう，定義されていったのか，わからなくなっちゃいそうです．切腹ー！

Dr.StrangeLab さんのレス (2005/01/17(Mon) 21:56)

確かに，磁界H[A/m]から磁荷qm[Wb]が受ける力F[N]を F = qm・H とするのはあまり教科書なんかにも出てきませんね． （ひょっとして高校の教科書には出てこない？） でもちゃんと次元は合っています．

電気のF = q・Eは実験で早くから分かっていたけど， 磁荷は存在しないから拙者も切腹！（笑）かな…と思いました． しかし，電気素量が計測されるまでは F = q・E を直接実験で確認するのは無理なような気もするし… ファラデーがそうなるように考えることにしたんだったかな？

＞電気のＦ＝ｑＥそっくり そうなんですよね．非常に対称性が高い． 電荷の単位クーロンは，アンペア×秒ですが， 磁荷の単位ウェーバーはボルト×秒で， この辺の対称性も萌え（笑）です．

かつ さんのレス (2005/01/17(Mon) 23:20)

みなさん，こんばんは．

> ファラデーがそうなるように考えることにしたんだったかな？

ファラデーが発見したのは，電気分解の法則ですよね． で，これはクーロン力の法則が先で，そこから，電荷が電場を作る 事からの論理的帰結なんじゃ無いかと．

やかん さんのレス (2005/01/18(Tue) 13:40)

かつさん，こんにちは．ご無沙汰してます(^-^) 私基礎知識がないくせに，昨日からインターネットと，本を読んで勝手に考えたりしてたのですが，いろいろ書いてあるのを見ると，ビオサバールの式も実験から得られた式で，ただ，サインとか入っているのは微小電線からの磁界の寄与が，クーロンの法則に似せて，同心球面状に広がるだろうことを前提に，電線に沿って，線積分した結果が，アンペールの法則に一致することをもってできたような事が書いてありました．考えてみれば２乗に比例，反比例ぐらいはまだしも，実験式にサインが出てくるなんて不思議だし，前提が入った上で既知の法則に矛盾しない，という事なんでしょうかね．だから，厳密には微小電線の及ぼす影響は測定できないけど，間接的には合っていると言う事になると書いてありました．チャパさんのお答えになるかどうかわかりませんが，したがってビオサバールの法則は，アンペールの法則に矛盾しないように作った実験式，という事らしいです．

• http://homepage2.nifty.com/eman/electromag/magnetic.html

そいでもって，本の巻末に書いてあった，線積分して，ビオサバールからアンペールにする式，こーれが，やかんの悲しさでわからない・・・． 電線上の微小線分Δｓと角θをなす方向に距離をｒ，電線への垂線の長さをR，垂線の足とΔｓまでの距離をｓとすると，

最後の定積分区間はπ/２から０までで，答えをもう片方の無限遠までということで ２倍すればアンペールの式になるらしいのですが，さあてどういう手順でθに置換積分 したんだかさっぱり・・．

かつ さんのレス (2005/01/18(Tue) 23:07)

やかんさん，こんばんは．

> クーロンの法則に似せて，同心球面状に広がるだろうことを前提...

そうでしたか．私も切腹．(A^^;)

> さあてどういう手順でθに置換積分したんだかさっぱり・・．

これは，本に書いてある通りで，s・tanθ＝R からでしょう． d tan(αθ)/dθ＝α・sec ² θ ですね．

やかん さんのレス (2005/01/19(Wed) 11:16)

かつさん，レス有難うございます．私，物理の法則って，あんまりきれいな形で教科書に載ってるものだから，なんか初めから人類が知ってたような錯覚に陥る事が時々あります．これも本の受け売りなのですが，クーロン力の式も，万有引力の式に似るだろう事は 予想しつつも，針金のねじれはかりを自分で考案し，慎重に実験したと書いてありました．きっと，計測したり，計算したりしながら”いいぞ，いいぞ，予測と合え！合え！，よっしゃああ！”とか言って作ったのでしょうか．ほんと，先人の努力はありがたいと思いました．

＞これは，本に書いてある通りで，s・tanθ＝R からでしょう． d tan(αθ)/dθ＝α・sec2θ ですね．

あ，有難うございます．タンジェントの微分はセカントの２乗になるんですね． サインがコサイン，コサインがマイナスサインまでは覚えていたのですが・・． また，３角関数の微積分やりなおさないとなあ．これでも高校の時はできたはずだったのですが・・・（実は当時もわかってなかったりして）．

チャパ さんのレス (2005/01/19(Wed) 18:21)

有り難うございます私の謝罪会見（タイトル）につきあってくれて・・・いや〜でもみんな切腹しすぎだよホント・・・（私の謝罪会見なのに・・・）Dr.StrangeLabさん有り難うございます．何とか私の理解できる範囲だったので何とか理解しました．これでやっと熟睡できる．やかんさん，かつさん，おこめさん，COさん有り難うございましたっぎり〜．では，私も・・・切腹！！！

Dr.StrangeLab さんのレス (2005/01/19(Wed) 20:07)

＞クーロン力の式も，（略）針金のねじれはかりを自分で考案し， ＞慎重に実験したと書いてありました． しかし，どうやってクーロンの時代に電荷量の絶対量を測ることなく 実験からあの式を導き出してきたのでしょうかね． 恐らくいろいろな電荷を帯びた球を捩り秤で距離を変えながら測ったのだと 思います．しかし，「距離の２乗に反比例する」は距離だけ変えればいいですが， 「電荷量の積に比例する」ところはどうやって示したのでしょう？ 金属球を接触させて同電位にする→表面積で静電容量が決まる…とかやったのかな？

やかん さんのレス (2005/01/20(Thu) 12:36)

＞「電荷量の積に比例する」ところはどうやって示したのでしょう？

あっ，そう言われてみればそうだ・・．電荷どうやってはかったんだろう？ そういえば電荷の１クーロンは電線間に及ぼす力で定義されたアンペアから定義した ものだから，それを考えても電荷は簡単に測定できなさそうですよね．どうやったんだろう？ ＞金属球を接触させて同電位にする→表面積で静電容量が決まる…とかやったのかな？

う〜ん，なるほどなあ・・．Dr.StrangeLabのおっしゃる通りの気がします．

Dr.StrangeLab さんのレス (2005/01/20(Thu) 23:20)

今日いろいろ考えたのですが，思考実験かも知れません．

＞金属球を接触させて同電位にする→表面積で静電容量が決まる…とかやったのかな？ 本当は電位の考え方はまだなさそうなので，前提として， 0-1）同じ大きさ，材質の金属の球Aと球Bを接触させる 0-2）金属なのでお互いに電流が流れる 0-3）AとBは同じ球なので，電荷にとっては区別できない →したがって，同じ電荷を帯びるはず

次に，思考実験１として， 1-1）球Aと球Bに働く力は作用反作用を考えると同じで逆向き 1-2）球Aと球Bを入れ替えても力は同じでなくてはおかしい 1-3）したがって，力は電荷の和または積に比例するだろう

さらに，思考実験２として， 2-1）球A○と球B●，球C◎を接触させ，同電位にする 2-2）球Aと離して球BとCを並べて配置した状態（○◎●）にする． 2-3）球Aと球Bの間に働く力をFとする．球Aと球Cの間にも同じFの力が働く． つまり，球Aは全体で2Fの力を受けている． 2-4）したがって，球Aが受ける力は相手の電荷量に比例する． 2-5）AとBを並べ，Cを単独にしても，同様の関係が成り立つ． これより，電荷の間に働く力は電荷量の積に比例する．

＞電荷の１クーロンは電線間に及ぼす力で定義されたアンペアから定義した アンペアの定義が先（真空中で１メートル離れて平行においた２本の導線に 等しい電流を流したとき， 500万分の１ニュートンの力を及ぼしあう大きさの電流．） で，A/sをクーロンとしていますから，確かにその通りです． 等しい電流…U字型配線にして測ったんでしょうかね．

やかん さんのレス (2005/01/21(Fri) 13:01)

なるほど・・．う〜ん，結構難しいですね・・． 確かに同材質，同形状の物は，同電荷に帯電する（MAXに帯電させる事ができたと考えて）という事や，接触させると等電荷になるだろう，という事が前提なんでしょうかね． 昔の科学者は本当に大変だったろうなあ．計算も筆算でやったんでしょうねえ．当たり前かもしれませんが，頭の良さだけでなく，相当な熱意がないと，出来ないことですね．

＞アンペアの定義が先（真空中で１メートル離れて平行においた２本の導線に 等しい電流を流したとき， 500万分の１ニュートンの力を及ぼしあう大きさの電流．） で，A/sをクーロンとしていますから，確かにその通りです．

良かったー！確かそうだと思っていたのですが，自信がなかったので安心しました！ Dr.StrangeLabさん，有難うございます．