岐阜人 さんの書込 (2005/01/07(Fri) 16:59)

この本のリーマン仮説を読んでいて「え？」と思ったところが有るんですが，なぜ ゼータ（−1）＝1+2+3+・・・・+k+・・・・，つまり自然数の和が−（マイナス）十二分の一になるのですか？何で−？何で整数ではないのですか？実際自然がこの事実を使っているということが物理のある分野で発見されたとも書いてあります．お願いします！

CO さんのレス (2005/01/08(Sat) 17:58)

こんにちは，岐阜人さん．

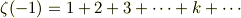
って本当ですか?? 私はこの分野に関しては素人ですが,それはおかしい気がします．

Riemann Zeta Function については次に詳しく書かれていますので一読してみて下さい．

• http://mathworld.wolfram.com/RiemannZetaFunction.html

このページで最初の方の(7)式に

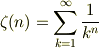
って書かれていますけど，こう書ける条件が(1)式の上に

On the real line with x > 1, the Riemann zeta function can be defined by the integral...(以下略)

と書かれています．要約すると， が 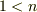の正の整数でなければ

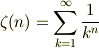
とは書けないということです．

もし 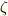関数で 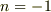の場合を計算するのでしたら，(69)式 〜(71)式のようになるみたいですよ．

岐阜人 さんのレス (2005/01/10(Mon) 13:38)

COさんありがとうございます．僕は今受験生でありましてそこを見てもさっぱり解りませんでした．自分の解らない事を人に尋ねてもダメですね．出直してきます．

CO さんのレス (2005/01/10(Mon) 13:57)

あ，受験生さんでしたか，これは失礼いたしました． さすがに英語ページをいきなりは厳しかったですね．(^^;

とりあえず，ゼータ関数が

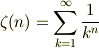
と書けるのは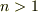， のときだけのようです．

したがって，

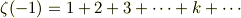
とは書けないということらしいです．

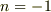のときは別な表記になるけど，それを計算すると 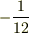という結果が得られるようです．