振り子
振り子
日常 さんの書込 (2004/12/05(Sun) 13:41)
初めまして.運動方程式,習いたての高専生1年です.物理苦手かもです. テスト近いので,入手した過去問を解いているのですが,いまいちわかりません. 下の問題なのですが,(1)と(2)の違いがわからず,(3)はできません; なんでもいいので書き込んでいただけると幸いです.
静止していた電車が動き始めたとき,天井につるした振り子の糸は鉛直方向と5度の角をなしていた.g=9.8[m/ss] (1)地上の観測者から見たとき,おもりにはたらく力を挙げよ. (2)電車の中の観測者からみたとき,おもりにはたらく力を挙げよ. (3)電車の地上にたいする加速度を求めよ.
慣性力の説明
おこめ さんのレス (2004/12/05(Sun) 14:04)
はじめまして,日常さん. (1),(2)の違いって高校生の時は正直よく分かりませんでした.えっとですね,要は運動を測る座標が電車と一緒に動くのが(2)で地球のある点に張り付いているのが(1)です.(2)のようなところから見るのを運動系で運動を見るっていうんですけど((1)は静止系),このとき見かけの力(慣性力)が働くんです.それがちょうど大きさが(3)でもとめる電車の加速度(振り子と電車は一緒に移動しているから加速度は振り子と同じです.)と振り子の質量の積で向きが逆になるんですよ.この問題の核心だと思うので,そこのあたりの事情だけ説明しておきます.
説明) 電車の加速度をaとしたとき(1)では運動方程式は
(質量)×(加速度)=力
で ma=F? 次に(2)のときも (質量)×(加速度)=力 ただし力はFと慣性力の和で (質量)×(電車から見た振り子の加速度)=F+慣性力 つまり代数で表すと ma'=F+F' と書けます.電車の上では振り子の加速度a’はゼロだから(電車の中から見ると振り子はずっと静止しているので速度もゼロ,加速度もゼロってことです) 0=F+F'? です. <b>(ポイント!!)</b>ここで?式と?式は同じ運動を表しているので全く同じ運動方程式であることを思い出してください!(同じ運動なのに違った運動方程式が成り立つ事は無いってことです.) ?と?式を比較すると F'=-ma? が成り立つことに気付く事ができます. (説明終わり) まとめ ?式が成り立つことについてもう一度まとめておきます 仮定) 1.運動方程式と運動との対応は1対1である. 2.振り子,観測者(座標系),電車の加速度がaで等しい 結論) 最後に?式を完全に言葉で書くと (振り子にかかる慣性力)=(振り子の質量)×−(地面に対する観測者の加速度) です.
日常さんはこういう説明が欲しかったのではないでしょうか?あとは上の問題に当てはめて問題を解いてみてください.
少々不親切な説明ですが・・・・まあ,頑張ってください.後この問題は振り子の問題とは思わない方が混乱しないと思いますよ.
Re: 振り子
CO さんのレス (2004/12/05(Sun) 14:18)
日常さん,こんにちは.
これは物理習い始めだと結構なやむ問題ですよね. (1)と(2)の違いは, (1)は,地上にいる観測者は静止しているので慣性力を見出しません.ただし観測者から見たおもりは加速度運動しています. (2)は,電車の中の観測者は加速度運動しているので慣性力を見出します.ただし観測者から見たおもりは静止しています. (慣性力が何なのか,は上でおこめさんが説明してくださっているようですね)
(3)は電車の中に乗った観測者から考えるのが便利です.図を書くとわかりやすいんですが・・
<pre>
/|
/ |
/θ|
/ | → 電車の進行方向(加速度 a)
/T |
/ |
f ←● |
/|
/ ↓
F mg
</pre>
うまく出てるかな.走っている電車の中の観測者は,このような力のつりあいの状況を見ています.
 は慣性力,
は慣性力, 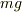 は重力
は重力  はそれらの合力で糸の張力
はそれらの合力で糸の張力 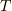 と釣り合っています.
図を睨むと,次の関係が見えてきます(見えて欲しい).
と釣り合っています.
図を睨むと,次の関係が見えてきます(見えて欲しい).
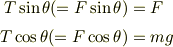
この二つの式を連立して 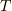 を消去し,
を消去し,  について解きます.慣性力
について解きます.慣性力  の大きさは
の大きさは 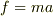 で書けるので,
で書けるので,  が求まるというわけです.
が求まるというわけです.
どうでしょうか?
# 慣性力は私も高校のとき,よくわからず悩んでました・・.
Re: 振り子
日常 さんのレス (2004/12/05(Sun) 17:30)
御二方,丁寧な説明ありがとうございます. 慣性力は,授業で聞いた覚えが・・・; 見かけの運動ですね.
明日,試験なので頑張ってみます. また疑問があったら,持ち込みたいと思います. ありがとうございました.
Re: 振り子
ブルー さんのレス (2004/12/06(Mon) 00:12)
日常さん,みなさんこんばんわ!!ブルーです.よろしくお願いします 日常さん,テストがんばってください!
おこめさんとCOさんが素敵な解答されたので,僕は精神論を・・・・・( ̄. ̄ )ボソ...
>物理苦手かもです 僕も最初はそうでした!しかし苦手だと思うのは,「物理ってぜんぜん面白くね〜よ」となる原因です.僕は高校2〜3年まで「苦手だから面白くない」と思ってましたし,それで勉強しなかったので全国模試で100点中20点なんてこともありました.しかし,物理に目覚めてからは90点くらい取れるようになりました.
どうしてこんなに物理がわかるようになったかというと,「物理はイメージだ!」ということに気づいたからです.物理ってイメージできれば「面白く」なります.そこで,「橋本流解法の大原則」という本を読んでみてください.物理が面白くなること間違いないです.
Re: 振り子
おこめ さんのレス (2004/12/06(Mon) 23:31)
>どうしてこんなに物理がわかるようになったかというと,「物理はイメージだ!」ということに気づいたからです.物理ってイメージできれば「面白く」なります.そこで,「橋本流解法の大原則」という本を読んでみてください.物理が面白くなること間違いないです.
僕が持っている高校の参考書は『橋元の理系物理頻出問題解法』だけですね.センター試験後に買いました.『橋元流解法の大原則』には手が出ませんでした.たしかけっこう分厚くないですか?(分厚い方が分かりやすいのでしょうけど)
Re: 振り子
崎間 さんのレス (2004/12/07(Tue) 01:03)
> 『橋元流解法の大原則』には手が出ませんでした. > たしかけっこう分厚くないですか?
ごく標準的な厚さだと思いますよ.読みやすい本だと思います.おこめさんくらいの知識があれば,立ち読みで全部読み通せる(練習問題は除いて)のではないですかね.
Re: 振り子
やかん さんのレス (2004/12/07(Tue) 13:36)
日常さん,みなさん,こんにちは.日常さん,試験お疲れ様でした! 以前,同じような話題があった時に,管理人さんが参考になるリンクをご紹介されたのを思い出しました.
- http://www.geocities.co.jp/HiTeens-Penguin/1552/comi_lecu/physics/phy-1350.html
- http://www.ne.jp/asahi/hanako/physics/lecture/dynamics/kansei_fig001.htm
- http://www.ne.jp/asahi/hanako/physics/lecture/dynamics/ensui_fig001.htm
でももうここではすでに,おこめさんやCOさんが,わかりやすい説明を充分されているので必要ないかもしれませんね(毎度わかってないのにお節介ですみません・・).
Re: 振り子
CO さんのレス (2004/12/07(Tue) 20:43)
けっきょく日常さんにはわかってもらえましたでしょうか? 試験がうまくいったことをお祈りしております.m(__)m
Re: 振り子
崎間 さんのレス (2004/12/07(Tue) 22:45)
> 以前,同じような話題があった時に, > 管理人さんが参考になるリンクをご紹介されたのを思い出しました.
やかんさん,よく覚えてらっしゃいますね.すっかり忘れてました(^^;
> 試験がうまくいったことをお祈りしております.m(__)m
同上です.
Re: 振り子
tomo さんのレス (2004/12/08(Wed) 18:34)
ちょっと気になったので自分の考えを書いてみます.
> (ポイント!!)ここで?式と?式は同じ運動を表しているので全く同じ運動方程式であることを思い出してください!(同じ運動なのに違った運動方程式が成り立つ事は無いってことです.)
「全く同じ運動方程式」という表現は,個人的には語弊があると思います. ?と?では式の意味が違うからです.つまり,(一つの運動を記述しているので) 「数学的には」全く同じ方程式が立つと言った方が良いのではないかと….
Re: 振り子
おこめ さんのレス (2004/12/08(Wed) 19:56)
>「全く同じ運動方程式」という表現は,個人的には語弊があると思います. そのとおりです.ただ高校生の方に『数学的には』と漠然と書くと???となってしまうかもしれません.うーん,適当な言葉が思いつきませんね.ごまかしの説明ですみません.
同じ方程式(数学的な方程式)を満たすということを強調したいあまりにこのようなあやまちをしてしまいましたが,本来ひらりとかわして(何もかかずに)説明すべきでしょうでしょうね.
Re: 振り子
tomo さんのレス (2004/12/09(Thu) 00:53)
> ただ高校生の方に『数学的には』と漠然と書くと???となってしまうかもしれません.
なるほど….確かにそうかもしれませんね. 難しいですね.分かってもらえるように説明するというのは.
Re: 振り子
yu さんのレス (2004/12/11(Sat) 22:04)
崎間さん,はじめまして. yuといいます.山本明さんのHPから流れてきました.
慣性力についてはかなり悩まされたので,相当思い入れ(恨み?)が強いです. 正直に白状すると慣性力のついてはっきり理解できたのは大学三年になってからだと 思います.(まだ理解してなかったりして,,,)
勝手ながらなぜ慣性力は見かけの力とよばれるものかを喋ってみたいと思います. 例えばよくある電車の例で考えたいと思います. ホームで電車が止まっているとき,扉付近の電車内にいる人(A氏)と プラットホームに立っている人(B氏)が向かいあっているとします. そのとき電車が急発進(加速度運動)するとA氏は後ろによろけることになります.
これからその現象を考えていきたいと思います. B氏からみたら,A氏はもともと止まっていたのだから止まり続けているのは 当然です.(これが慣性の法則の静止バージョンです.) だからA氏が急発進(加速度運動)するときに,B氏が後ろによろけるのは止まろうとする性質(慣性の法則)から当たり前のことになります. その一方で,A氏は急発進したことで後ろによろけたわけです.じゃあ,A氏はよろけた 理由をどこに求めたらいいのでしょう? まず考えなければならないのはよろけた以上,ma=F(ニュートンの第二法則)から 力を受けていなければなりません.じゃあ,だれがA氏を押したのでしょうか?
B氏からみたら,A氏はただ単にそこにとどまろうとしただけです. この立場から考えるにA氏は誰か(もしくは何かから)押されたわけでなく, ただそこにいようとしたのに,急発進(加速度運動)したせいでma=Fから 力を受けなければならないわけです(ただそこにいようとしたのにかかわらず,,,). だからこのような(まわりくどい言い方とすると慣性の法則を保とうとするために) 力を考えなければならなかったわけです.そのためこの力を慣性力と呼んだわけです. そして誰かに押されたり,重力,電磁力なんかとの力というよりは, 慣性の法則を保つようなものをホンモノ(!)の力と区別して見かけの力と呼びます.
ひじょ〜に,まわりくどい言い方をいいましたが, 非常に自然な考えです.(まわりくどいのは自分が変なこといろいろ考えちゃったせい)
,,,という感じで慣性力というものを理解しています.オカシナ点があったら 指摘してくれたらありがたいです.
Re: 振り子
おこめ さんのレス (2004/12/11(Sat) 22:37)
>慣性の法則を保つようなものをホンモノ(!)の力と区別して見かけの力と呼びます.
運動系から見た時に働く力と慣性系から見た時に働く力の差分を慣性力と言ったほうが分かりやすいかも知れません.そしたら”ホンモノの力”という造語をしなくてもすっきり説明できると思います.最後に結局,他の力と比較して説明しているので分かりづらいように思いました.(好みの問題かもしれません)