タイヤの力学
タイヤの力学
久家重允(くげしげまさ) さんの書込 (2010/05/29(Sat) 13:08)
70歳近くの元電気工学屋です(現役を離れて6年です.力学については工業高校程度です.)長年インターネットで調べましたが得心の行く記事が見つからなかったので投稿した次第です.
ゆっくりと水平に転がる質量m(kg)半径r(m)の車輪(タイヤ)が,段差h(m)の階段を乗りあげる場合,車輪に加えるべきトルク(N-m),又は車輪中心にに加える水平方向の力(N)は,どれくらいになるのでしょうか. 図や式を使ってご教示いただければ幸いです. また,タイヤと段差のところの摩擦係数は影響するのでしょうか?タイヤの弾性なども関係するのですか?ある程度の速度をもって,乗りあげる場合はどんな配慮が必要でしょうか?
Re: タイヤの力学
Yokkun さんのレス (2010/05/29(Sat) 23:42)
最も初歩的には,重力 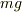 ,段差の角での抗力
,段差の角での抗力 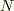 ,水平方向の力
,水平方向の力  のつりあいを考えればよいと思います.
のつりあいを考えればよいと思います.
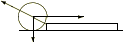
段差の角を軸とする力のモーメントのつりあいから,車輪中心と角を結ぶ半径の水平方向からの角度を  として,
として,
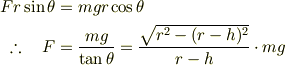
を得ます.すなわち,
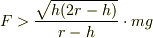
のとき,車輪が段差を上がります.下記はシミュレーションの動画です.
設定は, 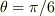 すなわち,
すなわち, 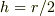 です.
ただし,以上の解析は,十分ゆっくりと引いた場合に上がる限界ということですから,速度をもって段差に衝突する上がり方では,また条件が異なると思われます.
です.
ただし,以上の解析は,十分ゆっくりと引いた場合に上がる限界ということですから,速度をもって段差に衝突する上がり方では,また条件が異なると思われます.
Re: タイヤの力学
甘泉法師 さんのレス (2010/05/31(Mon) 20:58)
こんにちは.Webで 仙台電波高専他 http://www.cc.sendai-nct.ac.jp/~ckuma/paper/chair/chair1_9808.pdf Q&A http://soudan1.biglobe.ne.jp/qa3896171.htmlを見つけました. ご参考になるでしょうか.
Re: タイヤの力学
Yokkun さんのレス (2010/05/31(Mon) 22:11)
甘泉法師さん,こんばんは.有用な情報をありがとうございます. 質問された方の反応はないようですが,
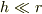 のとき,
のとき,
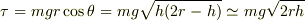
ということでしょうね.おかげさまで,計算ミスに気づきました.