novice さんの書込 (2010/05/27(Thu) 18:52)

物理のかぎしっぽの記事の読破率だけ反省しても，物理について私はまだ初歩的な部分しか理解できていないと思うのですが， 少なくともこれまでのところ，まったく理由を見つけられなかった疑問が１つあります．（とんちんかんな質問でしたらすみません）

<b>どうして物理学の理論表現に因果関係を表す記号を導入しないのでしょうか？</b>

物理学の理論は数学あるいは数理論理で表現される部分がほとんどなのだと思いますが， 標準的な数学での関数や関係，論理記号を用いるのに加えて，因果を表す記号を入れても いいように（素人考えですが）思われます．（「数学」には必要無いかと思いますが）

でもこういう物理学のテキストでは，因果関係の主張は数学的表現の意味には含まれず， 方程式の解釈とか理解とかいう，いわば数学の言外の部分に担わされているように思います．

明示的に因果関係を表す記号を導入しない理由をご存じの方がいらしたら教えてください． できれば，この疑問への回答を載せている成書などありましたら挙げていただけると幸いです．

novice さんのレス (2010/05/27(Thu) 18:52)

この掲示板の過去ログを検索させていただくと，過去にも関係するような話題があったようですが， ttp://hooktail.maxwell.jp/bbslog/21287.html ttp://hooktail.maxwell.jp/bbslog/20607.html 私にとっては答えがまだ見つけられていません．

私が推測する回答候補は a) 実は物理学者は因果関係に関心がなく関数関係だけが研究対象だから（「無関心」説） b) 因果関係を表現することはどんな論理体系であっても不可能だから（「不可能」説） c) 因果に関する言説を含めた物理学を記号表現するのはとっても難しくまだできる人がいないから（「未解決問題」説） d) 一部の分野ではすでに導入されているよ（「不勉強」説） e) 物理学での「因果」は常識とは違って周知の数学的関係（の組み合わせ）で定義されるからこれ以上の記号は要らない（「定義の問題」説） です． ・決定論が云々とか議論があるし，みんな因果的「解釈」がしたいのだからa)はないだろう， ・c)はまだしもb)には積極的な証明が必要でしょうから，そしてそのような証明を耳にしたことがないので，b)もないだろう， ・e)は，たとえば ma = F の "=" が右辺から左辺への因果だと定義する，など考えられますが，そうすると「解釈」は必要なくなりますからこれもないだろう， と予想しています．

トビラ．． さんのレス (2010/05/28(Fri) 08:41)

はじめまして

とても興味深く拝見させていただきました．

独創的な考えはとても好きだからです．

的はずれなことをいっているかもしれませんが，僕の考えも一応のせておきます．

まず因果関係を表す記号というからには，時間的に飛躍させる記号であることが理解できます．つまり時間の次元を持つ記号のように思えます．，，，とこの話はおいといて・・・・(笑)

まず因果率をかんがえるからには，そのパラメーターは時間でなくてはいけません． そこで時間をパラメーターとする運動方程式が与えられたら，解釈によってはある時間ａを境に二つの事象に別れる場合があります．ａより前の事象が原因で，ａよりあとの事象が結果です．

しかしこの境界条件(つまり事象の分かれ目)には任意性があり，因果関係をかんがえることは本質的ではないと思います． 本質的なのは，運動方程式などです． つまり物理学で大切な「計算」は本質的なものだけをもちい計算し方程式をたたきだします．そのあとの方程式をどのように解釈するかは人間の仕事であり，そこで事象の定義や今いった境界条件をもちい因果関係を理解すればいいと思います．そして数式に用いる記号は計算に役立つものである必要があります．しかし今いったように因果関係を示す記号は計算において不要なので(なぜなら本質的でないので)，そのような記号を導入してもなんの法則も得られないのではないでしょうか？(因果関係とは「原因と結果」という一つの結果を示していて，それに対し運動方程式は「原因と結果」の意味を示し，また同時に因果関係の原因である．と思います．なので因果関係は計算後にわかることなので，計算の途中に用いるものではない気がします)

その事は次のことからも言えると思います．つまり数式とは法則を扱うものなのです．因果関係を示す記号を導入して，その記号にどのような法則があるでしょうか？例えば不等号なら移項することや，両辺をマイナスで割ることにより，大小の関係が反転するなどの法則があります．集合論なら，∩や∪の法則として

Ａ∪Ｂ＝Ａ＋Ｂ−Ａ∩Ｂ

の法則が成り立ちます． このようにして数学に用いる記号には，それなりの法則がないと実用性がないんです．数学とは法則を扱う分野だからです．

計算に因果関係を表す記号を用いるなら，その記号にそれなりの法則が必要だと思いますが，僕が考え付く限りありません．ただ結果を分かりやすく表示するだけのように思います．

なので無理に導入する必要がないと思います． でももちろんあってもいいと思います．結果を分かりやすく表示するために．

ただ応用上は現段階では使えないと思います．いつかは使えるようになるかもしれませんが

novice さんのレス (2010/05/28(Fri) 13:05)

変な質問に答えていただいて恐縮です．

> 因果関係を示す記号を導入して，その記号にどのような法則があるでしょうか？

おっしゃりたいことを「法則」と呼ぶのは私には違和感がありますが，それはさておき，

一例として，私の素朴な分析によると，「引き起こす」を意味したい記号 C について ・ ∀x∀y( x C y → ¬(y C z) ) ・ ∀x∀y∀z( (x C y ∧ y C z) → x C z ) などの公理をおくことは，素朴な因果概念からの合意はできると思います． ご指摘のように時間パラメタを入れて ・ ∀x∀y∀z∀t1∀t2∀t3( ( x(t1) C y(t2) ∧ y(t2) C z(t3) ) → x(t1) C z(t3) ) などとしたほうがよいのかもしれません． 調べてみたところ，時間や因果の概念を入れた論理はすでに研究されているようなので (temporal logic や causal logic で検索してみてください)， 厳密な理論体系に因果概念を入れること自体は不可能ではないような気がします．

しかし，このように因果記号を導入するには，因果関係の relata (上のx, y, z) は何なのか，とか，どのような公理をおくべきか，など， いわゆる「物理学での」因果概念の分析をしなければならないと思うのですが，これについてマジョリティの物理学者はどう考えているのか， という点が私のよくわからない事の１つです．

> しかしこの境界条件(つまり事象の分かれ目)には任意性があり，因果関係をかんがえることは本質的ではないと思います．

事象の分かれ目の話はとても興味深いです． 離散時間ならまだしも，のっぺり連続の時間を措定して，物理学者はどうやって因果に言及するのかと不思議に思っていました． というのも，連続なので，ある時点t1のすぐ次の時点t2というのが無い(?)ように思います． あるいは，t1 ＜ t2 であるどのような2時点の組 (t1, t2) でも因果関係が成り立つ，と方程式を読むべきなのでしょうか．(物理学的には ＜ ではなく ≦ での定式化が標準ですか？？) でもそうすると，いわゆる因果「連鎖」という概念にそぐわないように思います． すなわち，t1 での状態が t3 での状態を「引きを起こした」とすると，どのような t1 と t3 の間にも t2 が存在するので， t3 での状態を「引きを起こした」のは t1 ではなく t2 の状態であり，t2 を引き起こしたのが t1 だと考えられますが， すでに明白なようにこの論理は無限に続きます．すると，t1 の状態が引き起こすのは「何」なのかを語れなくなるように思います．（有名なパラドクス？） この例では，relata を「状態」としましたが，「事象」とすれば回避できるのでしょうか？（「事象」の定義次第と思うのですが） あるいは連続時間マルコフ過程などをもっと勉強すればこの点については答えがあるのでしょうか？ もしや因果連鎖の概念が素人的な誤りで，物理学者はこの概念をとうの昔に捨てているのでしょうか？

また，「因果の矢」の問題と呼ぶのでしょうか，素朴な因果の概念からすると時間について考慮することは必要のように思われますが， 時間パラメタを入れただけでは我々の因果概念に一致するのに十分でなく，プラスアルファの何かが必要のように思います． それが ma = F が何か足りない理由のようにも思えます． たいていの物理学者は，この辺のことは無視しているのでしょうか．もしそうだとすれば，何故なのでしょうか？

> そのあとの方程式をどのように解釈するかは人間の仕事であり，そこで事象の定義や今いった境界条件をもちい因果関係を理解すればいいと思います．

このご指摘はとても示唆的だと思うのですが，そうすると，物理学の成果を活用するエンジニアような人たちが現場で物理学理論に因果関係を足して 使用するのが実状だ，ということならば，因果関係の主張は物理学理論には含まれていない，ということになりませんでしょうか？

> 数式に用いる記号は計算に役立つものである必要があります． や > なので因果関係は計算後にわかることなので，計算の途中に用いるものではない気がします など， 計算ができるかどうかや，計算での有益性について強調しておられますが， 物理の理論は物理世界の在り様を正しく記述することが，まずもっての目的であるはずだと思います． 在り様（一般的法則など）の記述が正しいことこそ，その変数に具体的な値を入れたもの（これが計算？）が現実を予測できる根拠ではないでしょうか． だから，記述が複雑になってしまって計算や予測が難しくなっても，それが世界の記述として正しいなら仕方ない，というのが物理学者の立場ではないかと思います．（工学者の立場かどうかは別です） このような立場からは，運動方程式などはたまたま単純な式で記述され応用が容易である幸運な例，と見なされるのだと思います． もしこの立場でいるならば，新しい理論的道具や対象を導入するかどうかは，計算が簡単なままにできるかどうかではなく，より正しい記述に近づくかどうかという基準が優先されるはずです．

因果関係に関する記号を明示的に導入することは，「この世界では何から何への因果関係が存在するがその逆はあり得ない」 というような命題について，それを方程式の言外の解釈（多義性）のようなものに任せず，理論に含めるということですから， 理論の厳密化（正しさへの近づき）には違いない思うのですが，どうでしょうか．

それと，お答えにある「計算」ですが，方程式から方程式が出てくるということで，式の変形や代入のような操作という意味で用いておられると理解したのですが， それによって出てきた方程式が「原因と結果」を表しているとのこと． しかし，おそらくそこには数学でよく見る記号（等号など）しかないでしょう．で，それを上述のように因果明示化するのであれば，ここに因果を表す記号が含まれていなければならず， そうすると，計算前の方程式（の組？）にもそれが含まれているか，途中の計算の規則に因果記号の導入則のようなものが入っていなければならなくなると思います． それが無い計算は，因果的に多義なものから多義なものを導出しているだけではないでしょうか．（この理解でおっしゃることをくみ取れていますか？）

novice さんのレス (2010/05/28(Fri) 13:08)

すみません．先の ∀x∀y( x C y → ¬(y C z) ) は誤りで ∀x∀y( x C y → ¬(y C x) ) です．

nabeyang さんのレス (2010/05/28(Fri) 13:54)

特殊相対論の範囲だと原因が結果を引き起こすという見方ができます．これは原因となる事象が先に起き，結果となる事象が後に起こるという意味です．しかし，因果律を満たすべしという法則は，特殊相対性理論の中には含まれていないそうです．(電磁気学，ニュートン力学は特殊相対論に含まれます)

yama さんのレス (2010/05/29(Sat) 01:34)

因果関係というと，事象Ａが原因となってその結果として事象Ｂが生じ，さらにＢが原因となって結果Ｃが生じ・・・といった因果関係の連鎖を考えられておられるのでしょうか？ しかし実際の事象の間の関係はもっと複雑で，単純に原因と結果が１対１に対応しているとは限りません． 例えば地球の運動を考えると，現在の地球の位置と速度によって未来の位置と速度が決まります．現在の位置や速度を変化させると，それに対応して未来の位置や速度も変化するので，現在の位置や速度が原因で，その結果が未来の位置や速度であると考えたくなります． しかし現在の地球の位置や速度を変えなくても，他の惑星の位置や速度を変えれば未来の地球の位置や速度は変化します．つまり未来の地球の位置や速度に影響する原因としては現在の地球の位置や速度だけでなく，他の惑星の位置や速度も合わせて考えないといけないわけです． さらに現在の地球の位置や速度は他の惑星の未来の位置や速度にも影響します． このようにいろいろな事象の因果関係は複雑にからみあっていて単純にＡ→Ｂ→Ｃ→・・・のような直線的な関係とは限らないわけです． もちろん太陽系全体の状態を１つの事象と見なせば，太陽系の全天体の現在の位置と速度によって未来の太陽系の状態が決まるので，その場合は直線的な因果関係の連鎖を考えることはできるでしょう．しかし太陽系全体の状態という複雑なものを１つの事象と見なすことが適切かどうかは疑問です．事象としては局所的で単純なものを考えるべきだと思います． さらにＡとＢの中間の状態とかその中間状態とＡとの中間の状態・・・というように無限個の状態が考えられるのでこれをどのように扱うかが問題になります．パラドックスが生じないような取り扱いが必要になるわけです．

もし因果関係を表す記号を導入していろいろな事象の間の因果関係を記述できたとしても，そのことにどんな有用性があるのかは疑問です． 単に因果関係があるというだけでなく，どんな関係があるかを導くことができ，それに基づいて未来の状態を予測できれば有用でしょう． しかし因果関係を表す記号だけを用いて，因果関係の有無以上の具体的な結果が引き出せるとは思えません．

これに対して現在の物理学では微分方程式によって状態の変化が記述されます． 微分方程式は無限小時間だけ隔たった状態を関係づけますが，それを積分することによって未来の任意時刻の状態を予測できます． いろいろな事象相互の関係も微分方程式を解くことによって導くことができます． つまりいろいろな現象は微分方程式によって適切に記述され，それを解くことにより有用な結果が得られるわけです．

このようなわけで，因果関係を表す記号を導入することについては，その必要性や有用性に疑問を感じます．

摩訶不思議 さんのレス (2010/05/29(Sat) 09:51)

> 因果関係の明示的表現 novice - 2010/05/27(Thu) 18:52 No.26802 > どうして物理学の理論表現に因果関係を表す記号を導入しないのでしょうか？

> Re: 因果関係の明示的表現  novice - 2010/05/28(Fri) 13:05  No.26810
> もしや因果連鎖の概念が素人的な誤りで，物理学者はこの概念をとうの昔に捨てているのでしょうか？

そのような記号の導入は，少なくとも物理にとっては不要だと思うが，なぜ「物理」だけにこだわるのかね？ 当然，化学関係の掲示板でも，次のように尋ねているはずだよね．

どうして化学の理論表現に因果関係を表す記号を導入しないのでしょうか？

ごく普通の論理的思考を持ち合わせていれば，物理だけにこだわる必要がないのは明らかだよね． 物理だけに因果関係を明示する記号の導入の必要性を唱えるとすれば，それはとても不思議不思議．

トビラ．． さんのレス (2010/05/29(Sat) 10:08)

さいあくだあああああぁぁぁぁぁぁっぁあ メッチャ書いて返信したのに，名前が入力されてませんって言われて，すべて消えた．さいあくだーーーーーー

あああああああああああああああああああああああああ

トビラ．． さんのレス (2010/05/29(Sat) 10:42)

もういやだ，・・・メッチャかなしい．．．とりあえず，とても重要だと思うところだけ書いときます．

はぁぁ・・・キーボードクラッシャーになりそう・・・・

＞物理の理論は物理世界の在り様を正しく記述することが，まずもっての目的であるはずだと思います． 在り様（一般的法則など）の記述が正しいことこそ，その変数に具体的な値を入れたもの（これが計算？）が現実を予測できる根拠ではないでしょうか． だから，記述が複雑になってしまって計算や予測が難しくなっても，それが世界の記述として正しいなら仕方ない，というのが物理学者の立場ではないかと思います．（工学者の立場かどうかは別です） このような立場からは，運動方程式などはたまたま単純な式で記述され応用が容易である幸運な例，と見なされるのだと思います． もしこの立場でいるならば，新しい理論的道具や対象を導入するかどうかは，計算が簡単なままにできるかどうかではなく，より正しい記述に近づくかどうかという基準が優先されるはずです．

はぁ・・・ここだけ返信しときます．はぁ・・・泣きたい，もう嫌だ・・・４時間くらいかけたのに・・・

とりあえず，ここだけ軽く返信します．結果からいいます．確かにそうだと思います． サイコロをふって，結果１が出る事象をAとします．その確率は

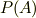
です．しかし，これにはサイコロを振る事象を明記すべきだと思います．厳密に言うと，サイコロの上が１である事象をAとして，そしてサイコロを振る事象をBとして，因果記号を→だとすると 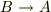となります．つまり，事象Bが原因で事象Aがおこる確率は

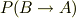
と表記すべきです．なぜなら，一般にはサイコロを振る事象なんていくらでも考えられます．例えば機械を使ってサイコロを放つ事象をB，地面に対し，１を上に向けてサイコロをおき，それに毎回同じ方向で似たような弱い衝撃を与えてサイコロを少しふる事象をCとおくと，一般に

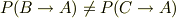
となるはずです．また，同様な考えにより事象Bがおこる確率を 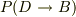とするなら，つまり，事象Dが原因で事象Bがおこる確率を用いるなら，事象Dが原因で事象Aがおこる確率は

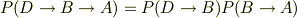
となります（多分，この場合条件付きの確率ではないと思うので）．よって，このように因果記号を導入することは必要に思えます．今はまだ現実的に実用化できなくても，人類が進歩し知能が複雑になれば使うと思います．

このように考えうる記号はなんでも導入すべきだと思います．数学の多様性のためにも．それに，その記号が役に立たないことを証明するにはありとあらゆることを調べてすべて否定してから言えることだと思うからです．

他にも，「因果関係」は「関係」の部分集合で・・・因果関係は情報の伝達なので時間パラメータは必要や，他にも状態の２つの解釈など語っていたんですが，もう嫌です．書きたくないです．泣きたい．メッチャ試行錯誤してまとめてたのに・・・最悪．（めっちゃ愚痴）

トビラ．． さんのレス (2010/05/29(Sat) 11:30)

とりあえず，ここも返信しておきます．

＞また，「因果の矢」の問題と呼ぶのでしょうか，素朴な因果の概念からすると時間について考慮することは必要のように思われますが， 時間パラメタを入れただけでは我々の因果概念に一致するのに十分でなく，プラスアルファの何かが必要のように思います． それが ma = F が何か足りない理由のようにも思えます． たいていの物理学者は，この辺のことは無視しているのでしょうか．もしそうだとすれば，何故なのでしょうか？

ma=ｆはただの関係で因果関係ではないと思います．この式の意味はa=f/mと式変形することによりわかりやすくなります．加速度aは，物質固有の量mに反比例するという意味で，どっちが原因でどっちが結果というものではないと思います．ただの関係だと思います．もしこの両辺に因果関係があるなら，ある時間の関数をC(t)とし，t=t_1のとき，C(t_1)=aで，t=t_2のときC(t_2)=f/mとなり，時間の方向を指定し，つまり，t_1<t_2なら，aが原因でf/mが結果ということになると思いますが，この方程式は，時間に対して不変なので，両辺が因果関係にあるということはないと思います．（どっちが原因でどっちが結果というのは時間の上下関係（どっちが先か）により決まることです．時間の上下関係がないのであればどちらが原因など言えないので，因果関係とは言えずただの関係だと思います）

＞このご指摘はとても示唆的だと思うのですが，そうすると，物理学の成果を活用するエンジニアような人たちが現場で物理学理論に因果関係を足して 使用するのが実状だ，ということならば，因果関係の主張は物理学理論には含まれていない，ということになりませんでしょうか？

これについても返信しておきます． 物理の方程式はまた，ある意味で因果関係の上を行く存在だとも思います．

まず，状態の２つの解釈について述べると，１つ目の解釈は，例えば，今どんな状態？って言われたら，「丸々な状態」，返信しますが，このとき用いている状態の意味はその瞬間における状態という意味です． それに対し，解析力学で現れる力学的状態とは，例えば

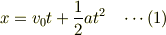
の運動を質点が満たしていれば，この方程式を満たすことをこの状態と呼びます．つまり，全時間の事象を含みます．

因果関係とは，前者の状態のことを意味します．それに対し，物理の方程式が示す状態とは後者を示します（もちろん例外的方程式もあります．たとえば固有状態のSchrodinger方程式）． 事象Aが(x_1,t_1)だとして事象Bが(x_2,t_2)だとして，それは(1)式を満足したとします．すると事象Aが事象Bの原因でこれが因果関係ですけど，これを時空図にすると２点になるのに対し，運動方程式（１）は線になります．なので，物理方程式は因果関係を内包するということになると思います．

トビラ．． さんのレス (2010/05/29(Sat) 11:54)

＞となります（多分，この場合条件付きの確率ではないと思うので）．

間違えでした．条件付きの確率です多分．なので，

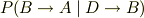
が，答えだと思います．また，事象Bと事象Cが原因で（ただし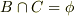， ）事象Aがおこる確率は

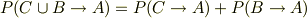
になりますね．また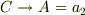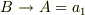， ， と考えると

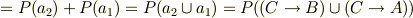
と考えることができるから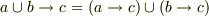， が証明できますね．（多分）

このようにしていくと，因果記号は必要ないような気がしてきますが（つまり，すべての事象を 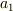や 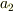と置き換え事象を再定義すればよい．），事象の細分化という点において，有意義なことのように思えます．それはまるで，テンソルやベクトルをもっとも基本的な量スピノールに分解するかのように．・・・ってそんなこともないか．もうなにがなんやら

トビラ．． さんのレス (2010/05/29(Sat) 17:20)

＞また，「因果の矢」の問題と呼ぶのでしょうか，素朴な因果の概念からすると時間について考慮することは必要のように思われますが， 時間パラメタを入れただけでは我々の因果概念に一致するのに十分でなく，プラスアルファの何かが必要のように思います． それが ma = F が何か足りない理由のようにも思えます．

これについて，自分の意見が間違っていたように思えてきたのでもう一度返信します． この世のすべての物理方程式を一つにまとめた 「万物の方程式」 があったとして，方程式の数をパラメータとしたなら，万物の方程式からEinseteinの方程式やSchrodingerの方程式に枝分かれしたなら，方程式の数が２になるわけですから，原因が万物の方程式で，結果がこの２つの方程式となり（たただし，パラメータの少ない数から多い数に方向をとる．），またこれから種々の方程式が導かれるけど，このようにして方程式の個数をパラメータにして，少ないほうを原因と解釈するなら，時間ではなくこれをパラメータにしてもいいように今思えました．

ただ，人間の思考を主観におくと，Schrodingerの方程式とEinseteinの方程式が原因で万物の方程式を導出できた．つまり，２つのものが原因で１つの方程式（結果）が得られたとも考えられますが（それは時間をパラメーターとした場合の解釈で），時間の向きとは標準理論によるとエントロピーつまり，情報量が少ない状態から多い状態に増える方向を指します．なので，方程式の個数が少ないほど情報量が少なく，方程式の個数が多いほど情報量が多いと考えると（つまり，エントロピーによりパラメーターの方向をきめ），個数のパラメーターを用いて方程式の因果関係を考えるとができるかもしれません．そこには以前僕がした時間の批判も必要ないように思えます． パラメータの選び方には任意性はあるもののエントロピーにより方向を決めてしまえば，因果関係が明らかになると思います． ・・・あれ？この場合の万物の方程式ってエントロピーが高い状態なのかな？よくわかんないです．

yama さんのレス (2010/05/29(Sat) 21:11)

方程式の数は，表し方によって変化します． 例えば１つの方程式 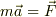も成分に分けて表せば

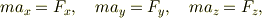
という３つの式になります． 成分で表しても次のように１つの式にまとめることもできます．

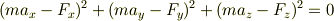
従って方程式の数をパラメータにするのは無意味だと思いますし，方程式の数と情報量やエントロピーは無関係だと思います．

novice さんのレス (2010/05/31(Mon) 12:44)

熱心な返信をいただき，ありがとうございます．

> ma=ｆはただの関係で因果関係ではないと思います．

私もそう思います．ゆえに，因果関係を述べるものはここには含まれていないな，と思ったので，冒頭の質問をさせていただきました．

> なので，物理方程式は因果関係を内包するということになると思います．

この点は，私の

>> t1 ＜ t2 であるどのような2時点の組 (t1, t2) でも因果関係が成り立つ，と方程式を読むべきなのでしょうか．

と同じ意味かと思います． そこで，yamaさんも

> さらにＡとＢの中間の状態とかその中間状態とＡとの中間の状態・・・というように無限個の状態が考えられるのでこれをどのように扱うかが問題になります．パラドックスが生じないような取り扱いが必要になるわけです．

とおっしゃっているのですが，物理学は，「中間」の状態を無視してはいないのだと思います． すると，物理学では，「時点 t1 の状態が引き起こすのは「何」ですか？」という質問にどう答えるのが標準的な見解なのでしょうか？

novice さんのレス (2010/05/31(Mon) 13:35)

> もし因果関係を表す記号を導入していろいろな事象の間の因果関係を記述できたとしても，そのことにどんな有用性があるのかは疑問です． > 単に因果関係があるというだけでなく，どんな関係があるかを導くことができ，それに基づいて未来の状態を予測できれば有用でしょう． > しかし因果関係を表す記号だけを用いて，因果関係の有無以上の具体的な結果が引き出せるとは思えません．

「AはBの原因である」と述べることは，「AはBの原因かどうかわからない」よりも，実践的にも有用だと私は思っていました． が，そうではないという考え方があるわけですね． すると yama さんとしては，私の言うところの a) 「無関心」説 が正しいということでしょうか．

このような立場からの返信をいただける方がいらっしゃったので，少々付け加えさせていただこうと思います． 私は，物理学はほとんど初心者に近いですが，私の知っている範囲では生物学などの自然科学や社会科学全般や医学・疫学などでは， いわゆる相関関係と因果関係は明確に区別されます． そして，このデータで主張できるのは相関関係（正確には変数間のdependence）まで，このデータでは因果関係を主張できる，などと いう判断が，ほとんどどんな研究でもなされていて，文の書き方に注意が払われます． つまり，そのような科学分野では主張に因果関係を含むかどうかはキーポイントであり，理論の有用性も変わってきます．

運動方程式などは，私からすると相関関係を述べているものに見えます． この方程式に因果関係の主張がトッピングされるとさらに有益になり，実際エンジニアはそのようにしてこれを活用しているのだと思います． それでも相関関係（関数関係）に加えて因果関係を述べることは有益ではないのでしょうか．

もし有益でないとすれば，そのような方程式の類をわざわざ因果的に「解釈」する必要性は何なのか教えてください．

novice さんのレス (2010/05/31(Mon) 13:56)

えー，このように，私は相関関係にプラスして因果関係を述べることは有益だと信じているのですが（さらに言えば物理学者や周辺分野の応用者も私に同じだろうと信じているのですが）， 方程式などの理論表現において，因果関係に関する複数の解釈の余地があって，その全部が正しいのではなく，ある解釈は間違っていて一部の解釈だけ正しい， という場合が（もしあるならば）問題だと思うのです． 上で ttp://hooktail.maxwell.jp/bbslog/21287.html を引用したのは，そのような一例を挙げたかったためです． このように，「こういう因果的解釈はダメで，こういう解釈ならよい」というきまりがあるのであれば，それを理論に含めて明言しておくべきだ，と思うわけです． それが，因果関係の記号を導入する一番の理由（もし導入するなら）だと私は思います．

トビラ．．さんは運動方程式について

> この方程式は，時間に対して不変なので，両辺が因果関係にあるということはないと思います．

とおっしゃっています．私もそう思います． 私は運動方程式を例に出しましたが，物理学の多くの分野を熟知している訳ではないので，時間に関して方向性をもつような例がありましたらご教示下さい． 私が知っているのは，熱力学のエントロピーの例のみです． つまり，私のいう e)「定義の問題」説の資格がありそうなのはエントロピーだけしか現時点で候補が見あたっていないのですが， エントロピーも「それが因果の本質である，その他の法則は方向性を規定しない関数関係だけだ」というような明示的な言説は見たことがありませんし（かぎしっぽにもありません）， 決定論などを議論する人が必ずエントロピーに言及しているかというとそうでもないようですので，物理学者の立ち位置がよくわからないのです．

もし「方向性を規定しない関数関係だけだ」というのが物理学の全部の法則に該当するなら， 物理理論は因果関係を含んでいないのではないかと思いました． でも，関数関係から因果関係を導出する標準的なやり方が物理学者の常識として共有されている可能性もあると思ったので（私は知らないので） もしあるならそれを教えていただきたいです． トビラ．．さんやyamaさんは代入や積分などの操作でそのようなやり方の提示を試みられたように思うのですが，satisfactoryではありません． なぜなら，その結果として得られる「t1の状態Aに続いてt2の状態Bになる」ということは，因果関係を意味するのに十分ではないからです．それも単に相関の記述です． たぶん，普通の数学的操作では，「引き起こす」という意味は出てこないのです．それは数学にそれを意味するものが含まれていないからで， 「引き起こす」を導入しない限り，数学的言語で表現できる命題が因果関係を表現することはないと思われます． そして，物理理論のどこかに「引き起こす」が含まれていないと，それは理論外から恣意的に持ち込んでいることになると思います． いかがでしょうか．

nabeyang さんのレス (2010/05/31(Mon) 15:09)

>ある解釈は間違っていて一部の解釈だけ正しい，という場合が（もしあるならば）問題だと思うのです．

結論からいえば，どんな解釈をしても構わないし，好きな記号を個人的に使って，物理学の問題を問いても問題ありません．問題ないというより，研究の現場では普通にやられていることです．問題設定によって，記号を変えたり，新しい概念を導入することはふつうのコトです．しかし，ある現象を解析するときに，その現象の起こる間，一度も変化しないような変数を変数として扱う人はあまりいません．それと同じように，因果関係といったものに対して，答えようとしていないときには，その記号は使う必然性はありません．

1グループあるいは1個人しか使わない記号も，用語，概念もあります．ファインマンによる経路積分量子化も，別に正準量子化という量子化の方法があったのですが，彼独自に開発した量子化の方法です(量子化の意味についてはわからなければ気にする必要はありません)．今では，ある問題については標準的に使われる方法です．

novice さんのレス (2010/05/31(Mon) 16:18)

典型的な例を見つけてしまったので，トビラ．．さん，確認させていただきたいのですが，

> ma=ｆはただの関係で因果関係ではないと思います．

この点，はてなキーワードによると， ttp://d.hatena.ne.jp/keyword/%B1%BF%C6%B0%CA%FD%C4%F8%BC%B0 因果関係だと述べられており，因果律を保証するとまで言われています． これはまったくの誤りということでしょうか．

暇なんだな〜 さんのレス (2010/05/31(Mon) 16:41)

つまらん話がよほど好きらしいな．

スレ主はよほどの暇人らしいｗ

novice さんのレス (2010/05/31(Mon) 16:58)

nabeyangさん，回答ありがとうございます． 2点確認したいのですが，まず

> 結論からいえば，どんな解釈をしても構わないし，好きな記号を個人的に使って，物理学の問題を問いても問題ありません．

物理学のテキストで登場する方程式などは<b>すべて</b>，どんな解釈をしても構わないようにできているのでしょうか？ 例えば，私が上でURLを挙げた過去ログでの議論のように，特定の解釈が誤りだとかいう言説はすべて間違いだということでしょうか？

また，2点目としまして，

> 因果関係といったものに対して，答えようとしていないときには，その記号は使う必然性はありません．

ここでおっしゃることは理解できるのですが，しかし， 私の知る限りのすべてのテキスト（かぎしっぽも含む）に，「因果関係」の記号は現れていません． 人々は皆，誰一人として，因果関係に興味がないのでしょうか（私にはまったく信じられないのですが）．

例えば，私が壁のスイッチをオンにすることが部屋の照明が点灯することを引き起こす，ということについて， 少なくともこれを作った人は因果関係を考慮に入れたはずだと思いますが， 因果関係の言葉を含まない物理学理論をどのように総動員すればこの現象を記述できるのでしょう． おそらく，因果関係を意味する言葉を導入しなければできない，という点は nabeyangさんには同意いただけるのではと思います． このように，日常的にも技術的にも因果関係を考慮しなければならない例はありふれている，と私には思われます． それにもかかわらず，関心がある人がいないとか，その作った人１人が独自に因果関係を理論に足して考えた，ということはないと思われるのですが． つまり，因果関係はごくごく少数の人の関心事ではなくて，大多数の人々の関心事ではないのでしょうか． すると，因果関係ぬきの理論もあっていいと思いますが，そこに因果関係を組み入れた理論がポピュラーでないのは変だと思われます．

ということで，もしや因果関係ぬきの理論から因果関係を組み入れた理論を，簡単に，誰しも同じように，導き出せる方法があるのでしょうか，という 疑念に行き着くわけです．もしあるなら，それが物理学の一部かどうかが，私の疑問への答えを左右するポイントかと．

交響曲第６番ロ短調OP.74 さんのレス (2010/05/31(Mon) 17:23)

>スレ主はよほどの暇人らしいｗ

暇というか自分の意見を正当化しようと必死だな．もはや笑いを通り越して悲愴感さえ漂ってくる．

nabeyang さんのレス (2010/05/31(Mon) 18:06)

>物理学のテキストで登場する方程式などはすべて，どんな解釈をしても構わないようにできているのでしょうか？

僕が「どんな解釈でも問題ない」と言った意味は，妥当な解釈ならば，どんなように解釈しても良いという意味です．もう一つ．もし妥当でない解釈だとしても問題無いのは，それは1個人が使っているものであり，それに文句を言う人もいないでしょう．鵜呑みしたり，誤解するのは，それを受け入れた人の問題だと思っています．

>このように，日常的にも技術的にも因果関係を考慮しなければならない例はありふれている，と私には思われます．

このように，といわれているのはむしろ論理学的問題だと思います．文中に登場するものが，物理学独自の概念を使ったところで，それは因果関係に関する論理の問題であって，物理学の問題ではないと思っています．日常的，あるいは論理的に正しく物理現象の因果関係について把握したことろで，物理的な問題に答えることには一歩も近づかないと思っています．(素朴な論理的整合性はもちろん，物理学的問題を解くときにも必要な要素です．)もちろんこれは，僕個人の意見であって，大多数の人がそうだという保証はありません．

なお，「物理的問題」や「論理的問題」などを厳密化して議論していったところで，それは物理の問題ではなく，物理学の解釈とか，論理の問題になるんだと思います．

トビラ．． さんのレス (2010/05/31(Mon) 19:18)

＞因果関係だと述べられており，因果律を保証するとまで言われています． これはまったくの誤りということでしょうか．

「（一定方向から）力が働く」＝「運動量が変化する」 です．運動量が変化すれば，力が働いていることになります．それが慣性の法則です．

力が働くのと運動量が変化するのとは同時だと思います．ニュートン力学だと物体に接触していなければ力は働きませんから．もし，力が働いた後，運動量が変化するのであれば，この方程式F=maは正しくありません．時間差を考慮にいれる必要があります．

「例えば，この式が正しいとして，先に力が加わるということは，力が加わった瞬間には運動量の変化は全くないということになります．運動量の変化が全くないということは力が加わったことにならないと思います．」

なので，この方程式が正しいと主張するニュートン力学の範囲だと，力が加わるのと運動量が変化するのとは等価で同時であると思います．

例えば，物体Aに物体Bがぶつかったとします．どちらも等速直線運動していました．Aに力が加わったから，Aの運動量がかわったともいえるし，Aの運動量が変わったから，Aに力が加わったとも言えると思います．「運動量の変化」が原因でない証拠はどこにあるのでしょうか？

それに，「運動方程式は時間反転に対しても成り立ちます」

なので，F=maは時間を反転させても成立するということになります．それはつまり，時間を巻き戻しした世界でもこの方程式は矛盾なく成り立ちます．そうなると，力が先駆けておこり，少し時間がたったのち運動量が変化するというこの方程式の解釈に矛盾が生じます．なぜなら，この解釈が正しいとすると，時間反転した世界では，運動量が先駆けて変化し，力が働くという式になり，これは，F=maと異なる方程式となるからです．しかし，時間反転した世界でもF=maは成立すると考えられているからです．

と僕は思います．ただ，僕より賢い学者がこのように書かれているということは，多分僕の考えが間違っているのでしょう．間違ったこと言って混乱させて，すみませんでした．（ペコペコ許してチョ）

しかし，

＞とおっしゃっています．私もそう思います．

とあなたも一応は発言してます．もちろん，そう発言させたのは僕が悪いんだとは思います．（でも，それでも僕は自分の意見が正しいと思います．）

＞私は運動方程式を例に出しましたが，物理学の多くの分野を熟知している訳ではないので，時間に関して方向性をもつような例がありましたらご教示下さい． 私が知っているのは，熱力学のエントロピーの例のみです

ちょっと言っている意味がわかりませんが，つまり，エントロピーの存在は時間に対して方向性を持っていると思っているわけですね？それに以前，特殊相対性理論では，時間反転に対しても，元の時間の方向の方程式が矛盾なくなりたつのような発言もされていたと思いますが，ちょっと誤解している気がします．例えば，エントロピーの話が理解できたなら，次のことも理解できる気がします．

宇宙論では，相対論が用いられます．その相対論は時間反転にていしても，粒子の運動は成り立ちます．つまり，「大げさな話」宇宙開闢（カイビャク）のときビッグバンが起こり，粒子が広がっていったとします．そして，何億年か後にすべての粒子の速度を同時に反転させるとします．それはつまり，時間を反転させることと同じことです．そうすると，ビデオテープを巻き戻ししているかのように，今まで起こった現象がそのまま巻き戻しされそしてやがては，ビッグバンをも再現し最後に一点に集まりもとに戻ります．そういう意味で，相対論は時間反転に対しても方程式が成立するという意味で，過去と未来とが全く同じで「区別できない」というわけではありません．開いた宇宙だった場合．相対論で計算すると，未来は星同士の間隔はすかすかになり，過去（宇宙開闢）ではすべての物質やエネルギーが一点に集まっています．大げさな話そういうことです．なので，相対論はエントロピーの問題を考えることができないのではないです．すべての物理現象は，多粒子系を考えることにより多分，多分ですがエントロピーを考えることができると思います．

つまり，関数関係だけの式でも，時間の方向性は方程式によっては決まってきます．

トビラ．． さんのレス (2010/05/31(Mon) 19:45)

yamaさんへ

＞従って方程式の数をパラメータにするのは無意味だと思いますし，方程式の数と情報量やエントロピーは無関係だと思います．

確かにそうですね．方程式の個数をパラメーターにするにはいささか無理がありました．でも，例えば，一般相対性理論と特殊相対性理論とでは，一般相対性理論の方が情報量が多い気がします．なぜなら，特殊相対性理論で計算できない現象も計算できるからです．このようにして，「方程式そのもののエントロピーや，情報量」のようなものは定義できないのでしょうか？ なんかできる気がします．

yama さんのレス (2010/06/01(Tue) 00:44)

>> さらにＡとＢの中間の状態とかその中間状態とＡとの中間の状態・・・というように無限個の状態が考えられるのでこれをどのように扱うかが問題になります．パラドックスが生じないような取り扱いが必要になるわけです．

>とおっしゃっているのですが，物理学は，「中間」の状態を無視してはいないのだと思います． >すると，物理学では，「時点 t1 の状態が引き起こすのは「何」ですか？」という質問にどう答えるのが標準的な見解なのでしょうか？

時間は連続的なので，ある時刻の直前とか直後の時刻というものはありません．従ってある事象の直前の事象とか直後の事象というものもありません． 「ある事象が起きるとき，その直前にそれを引き起こす原因となる事象があるはずだ．」という考え方は的外れであって，その考え方を貫こうとすればパラドックスが生じるでしょう． 状態が引き起こすのは「何」かというのは，このような考え方を前提にしているように思われるので，何とも答えようがありません．

物理学では，状態の変化のしかたは，普通は微分方程式で表されます． 微分方程式は無限小時間だけ離れた状態を関係づけるわけですから因果関係を含んでいるともいえますが，因果関係といっても上記のようなものではなく，原因と結果が連続的につながっているわけです．

>「AはBの原因である」と述べることは，「AはBの原因かどうかわからない」よりも，実践的にも有用だと私は思っていました． >が，そうではないという考え方があるわけですね． >すると yama さんとしては，私の言うところの >a) 「無関心」説 >が正しいということでしょうか．

因果関係の有無は大抵の場合は式を見れば分かるし，特に強調したいときは言葉で説明すればいいので，特別な記号は必要ないということです． 例えば，時刻0のとき初速度v0で真上に投げられた物体の時刻tでの速度vは，この初期条件の下で運動方程式 ma=-mg を解くことにより v=v0-gt と求められます． 速度vが初速度v0の関数になっているので，速度と初速度の間に因果関係があるのは一目瞭然であって，特別な記号で因果関係を表すまでもないでしょう．

>私は，物理学はほとんど初心者に近いですが，私の知っている範囲では生物学などの自然科学や社会科学全般や医学・疫学などでは，いわゆる相関関係と因果関係は明確に区別されます． >そして，このデータで主張できるのは相関関係（正確には変数間のdependence）まで，このデータでは因果関係を主張できる，などという判断が，ほとんどどんな研究でもなされていて，文の書き方に注意が払われます． >つまり，そのような科学分野では主張に因果関係を含むかどうかはキーポイントであり，理論の有用性も変わってきます

その通りです．しかしその場合の因果関係は言葉で説明されていて特別な記号は使われません． また物理学のように変化の過程を式で表すことができれば言葉による説明も必要なくなります．例えば何かが原因となって発病し，病状が進行していく過程を方程式で表すことができれば，因果関係は方程式の中に含めることができます．

>運動方程式などは，私からすると相関関係を述べているものに見えます． >この方程式に因果関係の主張がトッピングされるとさらに有益になり，実際エンジニアはそのようにしてこれを活用しているのだと思います． >それでも相関関係（関数関係）に加えて因果関係を述べることは有益ではないのでしょうか．

運動方程式は物理量の間の相関関係を表していますが，これは微分方程式なので物理量の時間的な変化の仕方を記述します．その意味で因果関係を含んでいます． それ以上どんな因果関係をトッピングするのでしょうか？ といっても運動方程式に含まれるのは完全な因果関係とは言えません．時間反転すると原因と結果が逆転しますが運動方程式は時間反転に対して対称なのでどちらが原因でどちらが結果かは運動方程式だけでは決まらないからです． そのあたりはトッピングの余地があるかもしれませんが，時間の向きについては別途検討が必要でしょう．

>例えば，私が壁のスイッチをオンにすることが部屋の照明が点灯することを引き起こす，ということについて少なくともこれを作った人は因果関係を考慮に入れたはずだと思いますが，因果関係の言葉を含まない物理学理論をどのように総動員すればこの現象を記述できるのでしょう．

それは言葉で説明すればいいでしょう．物理学で因果関係の言葉を用いてはいけないとは言っていません．特別な記号は必要ないということです．

yama さんのレス (2010/06/01(Tue) 01:05)

トビラさんへ

>このようにして，「方程式そのもののエントロピーや，情報量」のようなものは定義できないのでしょうか？

もしそのようなものが定義できたとしても，方程式のエントロピーと，その方程式によって記述される物理状態のエントロピーは関係ないように思います．