初心者 さんの書込 (2010/05/11(Tue) 19:01)

今期から非圧縮性流体を学び出した大学生です． 疑問に思ったことがあったので質問させていただきます．

ポテンシャル流では複素ポテンシャルが定義できるとありました． そして，その基本解として一様流，吹き出し，吸い込み，渦の複素ポテンシャルが書いてありました．

そこで疑問に思ったんですが，ポテンシャル流は渦なし流れなはずなのになぜ渦の複素ポテンシャルが存在するのかまったく意味がわかりません．

あと，渦度と渦って別物なのでしょうか??

回答よろしくお願いします．

ASA さんのレス (2010/05/12(Wed) 12:07)

>渦の複素ポテンシャル 記憶があやふやですが，これって円柱周回の一様流じゃないですか？

>ポテンシャル流は渦なし流れ こっちの渦は，局所的な旋回(渦巻き)で中心は任意の位置で，数に制限はなしだったと思います．

toorisugari no Hiro さんのレス (2010/05/12(Wed) 12:08)

> そこで疑問に思ったんですが，ポテンシャル流は渦なし流れなはずなのになぜ渦の複素ポテンシャルが存在するのかまったく意味がわかりません．

複素ポテンシャルが解析関数であるには，渦なしのほかに非圧縮性も要求されますが，「吹き出し，吸い込み」があるのは変ですね．こちらも問題です．

吹き出し，吸い込み，渦は全域で渦なし，非圧縮性を満たすわけでなく，特異点(原点)以外の領域でのみ「渦なし，非圧縮性」を満たす解なのです．

これらの特異点は，流体領域でなく，円柱などの非流体領域におかれるので，流体領域では渦なし非圧縮性を満たすと考えられます．

つまり，物体や境界に渦や湧き出しが隠れていると考えます． これは，電磁気学で「鏡像法」を学んだ方なら違和感を持たないと思います．

ASA さんのレス (2010/05/12(Wed) 15:16)

検索したら>ttp://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1214457872 この回答が参考になると思います．

No.26744への補足 >円柱周回の一様流 円柱を置くのは，特異点(原点)を避けるため，一様は流れに対して横の変化が0という意味．従って，渦度(局所回転量)rotV=0で渦なしとなっており矛盾はしてません．しかし，上の回答にあるように原点周りの循環(閉曲線量)は，0ではありません．循環でも流れの旋回量(曲がり具合)を表わせることが紛らわしさの要因ですね．概念的に違うものなのでしっかり区別しましょう．

ASA さんのレス (2010/05/12(Wed) 16:20)

訂正します． >一様は流れに対して横の変化が0という意味 説明が変ですね．原点周りの回転流で，たまたま，渦度が0，つまり∂xVy-∂yVx=0が成立する場合．具体的には，Vx=ay/r^2,Vy=-ax/r^2,|V|=a/r^2.流れの大きさが距離の2乗に反比例する場合ですね(ちなみにポテンシャルはφ=a/r;2次元流)．

ASA さんのレス (2010/05/12(Wed) 19:47)

ミスが多いな(2次元だから以下が正しい)． >|V|=a/r.流れの大きさが距離に反比例する場合 原点周りの循環Γ=2πaであり距離rに関係ない定数(これが一様な回転流）．

ASA さんのレス (2010/05/12(Wed) 20:10)

まだ，間違いがあった． >流れ関数ψ==aLogr，ポテンシャルはφ=-a*arctan(y/x)，△ψ=0,△φ=0

ASA さんのレス (2010/05/12(Wed) 20:50)

補足 循環Γ=2πa;一定と，角運動量L=mvr;一定とを対比させて， |V|=a/r.流れの大きさが距離に反比例する場合を自由渦(角運動量変化をもたらす力がないという意味)と呼ぶケースもあるようです．

初心者 さんのレス (2010/05/12(Wed) 23:43)

＞ASAさん 回答ありがとうございます． つまり「渦」は回転流のことであり流れの状態を示していて， 「渦度」は空間の各点における物理量という解釈でよろしいですか？？

あと，最後の補足の循環ΓはΓ=2πa・Vθですよね?? （Vθが一定であれば）

＞toorisugari no Hiroさん 回答ありがとうございます． なるほど，特異点が非流体領域におかれるから流体領域ではポテンシャル解析ができるという考えだったのですね．非常に納得しました．

あと物体や境界に渦や湧き出しが隠れているという考え方は目から鱗でした． 恥ずかしながら，鏡像法は先ほどネットで調べて知りました． この前勉強したフーリエ級数の半区間展開に考え方が似ていると感じました．

ASA さんのレス (2010/05/13(Thu) 06:34)

>あと，最後の補足の循環ΓはΓ=2πa・Vθですよね?? 今の場合，渦の強さを示す循環Γは定数なのでΓ=2πaでよいはず． 参照>ttp://ibis.mach.me.ynu.ac.jp/Matsui/Lecture/FD2/FD2-8.pdf

toorisugari no Hiro さんのレス (2010/05/13(Thu) 10:53)

> 循環ΓはΓ=2πa・Vθですよね??

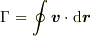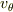ですから，閉経路が半径 の円周で速度の角度方向成分 が一定なら，おっしゃるとおり 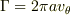となります．

ASA さんのレス (2010/05/13(Thu) 11:31)

toorisugari no Hiro さん ノーテーションや参考文献をちゃんと確認してからコメント願います． No.26748やらNo.26750で |V|=a/r.とaは，回転の強度を示しています． aは半径ではありません． No.26752の参考文献(8.2.3循環)との対比をすると，文献では|Vθ|=Γ/2πrとなってますが，ここでのノーテーションでは，|V|=|Vθ|ですから， 比較してa=Γ/2πを得ます． 変形してΓ=2πa(No.26748の式)となってます．

toorisugari no Hiro さんのレス (2010/05/13(Thu) 19:48)

> |V|=a/r.とaは，回転の強度を示しています．aは半径ではありません．

|V|=a/r.で定義される「回転の強度」という変な概念は初めて見ました． 参考文献にもそのような記述はありませんし．

なお，参考文献での循環の定義は通常の循環の定義と符号が逆になっていますね．

ASA さんのレス (2010/05/13(Thu) 21:05)

> |V|=a/r.で定義される「回転の強度」という変な概念は初めて見ました． 書き方が悪かったかな？以下""内のような追加があると誤解し難かったかも． >>No.26748やらNo.26750で |V|=a/r.と"．ここで"aは，回転の強度を示しています． これでaが半径を示しているとは，普通思いませんよね． toorisugari no Hiroさんには，aが，速度|V|の比例定数であって，回転流である今の場合その強さを表わしていることが理解できないのでしょうか？ 念のため説明しておきます． 位置ベクトルr~と速度ベクトルV~の内積はr~・V~=0であり原点を中心とする回転流となってます(No.26747Vx=ay/r^2,Vy=-ax/r^2より)． V~=(yf(r),-xf(r))であるときは，原点での回転流れですが，f(r)=r^(-2)のときだけ，rotV~=0(渦度0,渦なし)になります． このとき，原点を含まない場合の循環は0ですが，特異点である原点を含む閉曲線での循環は，ある定数となります(どこでも渦なしだからといって，どんな循環でも0になるとは限らないケースであり，循環と渦度の違いが明確になる事例ですね)． 参照>ttp://hooktail.sub.jp/vectoranalysis/MultivaluedPotential/ この循環の大きさは，速度の比例定数(ここではaを採用)で示されます． そして，この循環の大きさが渦の強度を表わすことは，紹介した参考文献にも「Γ:渦の強さで「循環」circulation と呼ばれる*2．」と説明されてますよ(参考文献もよく読みましょう)． Γ=2πaであるので，比例定数aを「回転の強度」と看做すことは，変ではありません(電磁気で例えれば単位系の違いにすぎない)．後，循環は角運動量と対比され，完全流体での保存則が説明されます(渦度が対応関係にあるわけでないことに注意)． ご理解いただけたでしょうか？ いずれにせよ，初心者さんが混乱しかねないので，ノーテーションや参考文献をちゃんと確認してからコメント願います．

ＡＳＡ さんのレス (2010/05/14(Fri) 07:10)

補足 渦なし流れは，rotV~=0である流れとされます． V~(y,0)というｘ軸方向のみの流れでは，流線は曲がっていてませんけどrotV~≠0であり渦あり流れということになります(循環も0でない)．

toorisugari no Hiro さんのレス (2010/05/14(Fri) 15:28)

> aは，回転の強度を示しています．

了解， はパラメータね． でも，へんなノーテーションですね．

> 初心者さんが混乱しかねないので，ノーテーションや参考文献をちゃんと確認してからコメント願います．

お返しします．

ポテンシャル渦は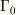， を定数として，

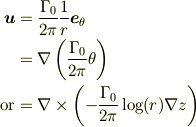
で定義されます．(参考文献とは符号が違います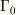．) を渦の強さといい，循環

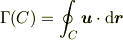
の値は閉曲線 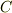で囲まれる領域に原点が含まれるなら 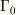それ以外は になります．

参考文献でも 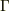をパラメータとして使っているのに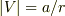， でポテンシャル渦を定義するから誤解が生じるのではないですか?

ＡＳＡ さんのレス (2010/05/14(Fri) 17:09)

>参考文献でもをパラメータとして使っているのに，でポテンシャル渦を定義するから誤解が生じるのではないですか? 違います． 時系列順に回答を追ってみるということを是非学んで下さい． あなたの考えは，時系列を無視した考えです． (わかっている人は，いいのですが，初心者の方々は，まず混乱します．） こでのノーテーションでは， １．No.26747で最初に "原点周りの回転流で，たまたま，渦度が0，つまり∂xVy-∂yVx=0が成立する場合．具体的には，Vx=ay/r^2,Vy=-ax/r^2" と強度パラメータとしてaを導入してます． ここで説明の流れは，まず，渦なし流れでのＶ~(回転流)を具体的に与ます． ２．No.26752で参考文献を紹介する． ３．その後でNo.26754，一般的な定義によるΓ(強度)とaとの対比をさせて，次に，それが循環量(閉曲線上の線積分で与えられる)と一致していることを確認させる． という流れになってます(この流れの途中で，物理的に重要な角運動量との関係にも触れました)．

ですから，このような流れを無視した頓珍漢なコメントは，スレ主の初心者さんを含む初心者の方々に混乱を与えると思います． 数学的に定義からはじめるなら，ポテンシャル渦の定義をぽんと置くだけで済むのですが，この方法だと，初心者の方々では，物理的イメージがよく判らなかったり，概念的にも未整備のため，何が何に対応するがわからなくて混乱したりする訳です． だからこそ質問のスレが建ったわけですよ(教科書読めで済まないからこそ)． この辺の事情をtoorisugari no Hiroさんには，ちゃんと理解した上で，コメントして欲しいと思います(ほんと"お返しします．"とか何考えてんの)． わかっている人向けの説明をしているわけではないのですよ． (わかっている人が，よく流れをフォローせずに(流儀が違うから)誤解しても，それは勝手ですが，しかし，誤解したまま変なコメントをするのは，明らかに迷惑なので，やめて欲しいと思います）

ＡＳＡ さんのレス (2010/05/14(Fri) 17:35)

補足 V~(|y|,0)というｘ軸方向のみの流れでも，流線は曲がっていてませんけどrotV~≠0であり渦あり流れですが，x軸上(y=0)のある点を中心とした円で循環を計算すると0になってます．「渦あり流れだから，循環もノンゼロ」とは限らない例です． 大域的な流線の様子と渦度(局所量)と循環(領域量)との関係は，こんなとこでしょうか．

初心者 さんのレス (2010/05/15(Sat) 18:17)

すみませんちょっとついていけてないです…笑

aは勝手に半径だと思い込んでいました． No.26747のVx等をみるとaが長さの次元では無いっていうのは明らかでしたね…