Maxwell応力
Maxwell応力
asdf さんの書込 (2010/04/22(Thu) 02:13)
無限に大きい平板に,面密度σ (>0)で電荷が一様分布している. このとき面に働くMaxwell応力を求めよ.
という問題なのですが,どう求めたらよいかまったく分かりません.
どうやればよいのでしょうか?
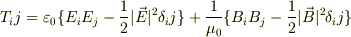
にEとBを代入すればいいのでしょうか?
しかし,Eは分かるのですが,Bの求め方がわかりません・・・
よろしくお願いします.
Re: Maxwell応力
asdf さんのレス (2010/04/22(Thu) 15:18)
回答ありがとうございます.
板がxy平面にあるとして計算してみたところ, Eはz方向のみで大きさが
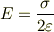
となりました.
そして代入して求めようと思ったのですが, Eは上下両方向に働くためどのように代入したらいいかよくわかりません. また, そもそもMaxwell応力とは何を求めたらよいのでしょうか. テンソルTを求めればよいのでしょうか?
一応自分は上下別に代入し,その和を答えにしてみましたが, それでよいのでしょうか? ちなみに値は
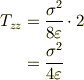
となりました.
Re: Maxwell応力
SP1 さんのレス (2010/04/22(Thu) 17:53)
普通,Maxwell応力というと,3×3の行列で書ける2階のテンソル 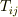 を指します.
問題では電流も時間変動する電場もないので,磁場Bは0になります.
電場Eはz方向のみ(ただし±の2方向)で,ガウスの法則から
を指します.
問題では電流も時間変動する電場もないので,磁場Bは0になります.
電場Eはz方向のみ(ただし±の2方向)で,ガウスの法則から 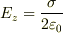 となります.
他の成分は0なので,
となります.
他の成分は0なので, 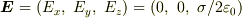 となるので,
となるので,
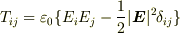 に代入すると,
に代入すると,
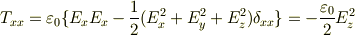
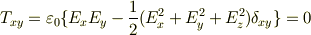
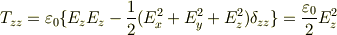
,
のようになり,結局 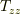 は,
は,
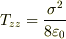 となるはずです.
z方向の電場のベクトルは2つありますが,片方だけで考えればいいです.(もう1つのベクトルは
となるはずです.
z方向の電場のベクトルは2つありますが,片方だけで考えればいいです.(もう1つのベクトルは 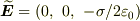 )
よって和を取ることもしません.(1つのベクトルから得られるテンソルに対して,別のベクトルからのものとの和を取る(2倍にする)理由が説明できますか?)
残りの成分も同様に求めればいいです.
間違いがあれば,あとは他の方,フォローをお願いします.
)
よって和を取ることもしません.(1つのベクトルから得られるテンソルに対して,別のベクトルからのものとの和を取る(2倍にする)理由が説明できますか?)
残りの成分も同様に求めればいいです.
間違いがあれば,あとは他の方,フォローをお願いします.
Re: Maxwell応力
asdf さんのレス (2010/04/22(Thu) 21:47)
ありがとうございます.
なぜ,片方だけで考えることができるのでしょうか?
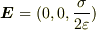 を代入したTと
を代入したTと
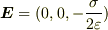 を代入したTは
同じ値になりますが,これは,2つの式が同じもの(マクスウェル応力)を表しているということでしょうか?もしそうなら,なぜそうなるのでしょうか?
を代入したTは
同じ値になりますが,これは,2つの式が同じもの(マクスウェル応力)を表しているということでしょうか?もしそうなら,なぜそうなるのでしょうか?
テンソルはややこしくてよくわからないです・・・
Re: Maxwell応力
SP1 さんのレス (2010/04/22(Thu) 22:35)
ええ,この場合はどちらで計算しても,応力テンソル自体は同じ値になります.
しかし,元々のベクトルで考えると,+方向のベクトルから求めた応力テンソルは+z方向を法線ベクトルとする面(表の面)に,-方向のベクトルから求めた応力テンソルは-z方向を法線ベクトルとする面(裏の面)に,というように,まったく異なる別々の面に働く応力テンソルというのがわかると思います.
ですから,応力テンソルは,1つのベクトル毎に個別に考えるべきです.
問題の答の書き方としては, 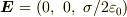 と
と 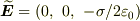 で個別に計算して,どちらも同じ成分の応力テンソルが得られたとすれば,問題ないはずです.
仮に
で個別に計算して,どちらも同じ成分の応力テンソルが得られたとすれば,問題ないはずです.
仮に 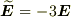 であれば,各ベクトルから得られる応力テンソルも異なる値になるのがわかると思います.
この問題では,
であれば,各ベクトルから得られる応力テンソルも異なる値になるのがわかると思います.
この問題では, 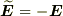 なので,応力テンソルが同じ値になるわけです.
なので,応力テンソルが同じ値になるわけです.
Re: Maxwell応力
なんとなく さんのレス (2010/04/23(Fri) 02:41)
横レス失礼します.
応力というのは力のベクトルとそれが働く面のベクトルで決まるものですから,今のように無限に薄い平面は一面しか無いように見えてイメージしにくいのかも知れません.少し幅(厚さ)を与えて考えてみてはどうでしょう. この無限平面導体にはびっしり面密度σの電荷があるとします.同符号ですから反発しあいます.つまり,平面を押し広げる力となります.平面に垂直(Z軸)には,その幅を広げるように働くので,膨らむ感じになります.とつレンズの腹のように両側に.ただし,無限に一様なのでどこでもそうですから,実際は平面のままです.一方平面に平行にも力が働きますが,無限に広いこと,もともと厚さが0なために,何の変化もできません. この両側というのが同じ力のベクトルの反対向きの面に生じる応力の正体です.力の向きも面の向きも逆方向なので同じ応力となります.
Re: Maxwell応力
asdf さんのレス (2010/04/24(Sat) 17:49)
では,結局答えの書き方としては,(途中式は省略しています)
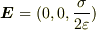 のとき,マクスウェル応力Tは,
のとき,マクスウェル応力Tは,
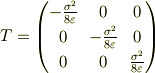
また, 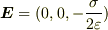 のとき,マクスウェル応力Tは,
のとき,マクスウェル応力Tは,
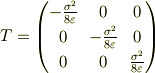
である.
という感じでよいでしょうか.
Re: Maxwell応力
SP1 さんのレス (2010/04/24(Sat) 22:49)
それでいいと思います.
最初に個別に計算すべきと言えばよかったですね.
片方でいいと言ったので混乱させたかもしれません.
なんとなくさんも補足説明してくれていますが,背中合わせの表の面と裏の面(厚さのない面ですが)を引き離すように応力が働きます.(  )
その他,xy平面にも応力テンソルの成分がありますが,直感的にはゴムのような面が
)
その他,xy平面にも応力テンソルの成分がありますが,直感的にはゴムのような面が 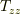 で面に垂直に引っ張られると,その引っ張られる中心(ここをxy平面の原点とする)に引き込まれるようになるのがわかると思います.
(水飴のようなドロドロしたものを垂らす様を思い浮かべるのもいいかもしれません)
あとは,応力について,弾性体力学や流体力学の本などで調べてみてください.
で面に垂直に引っ張られると,その引っ張られる中心(ここをxy平面の原点とする)に引き込まれるようになるのがわかると思います.
(水飴のようなドロドロしたものを垂らす様を思い浮かべるのもいいかもしれません)
あとは,応力について,弾性体力学や流体力学の本などで調べてみてください.