軌道と固定部分群の定理
軌道と固定部分群の定理
tanabe さんの書込 (2010/04/17(Sat) 10:14)
はじめまして. 群論の初歩について勉強させて頂いてます. とてもわかりやすい内容で大変助かっています.
さて,以下のとおり質問させて頂きたいことがあります.
(1)home > 代数学 > 固定部分群
固定部分群と軌道の関係
「定理群 G が集合 M に作用するとき, M 上の一点 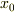 に関し,
に関し, 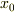 の G による軌道
の G による軌道 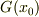 と, G の
と, G の 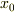 に関する固定部分群
に関する固定部分群 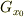 とが一対一に対応します.」
とが一対一に対応します.」
これに続く「証明は次のように考えます.」でいわれる証明とはこの定理に関するものでしょうか. 定理の内容と証明される内容と違っているように見えます.その証明は,この定理の次に書かれている定理のものと思われます.
また,この定理では, 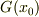 から
から 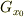 の上への一対一の写像がある,ということを言われているのでしょうか.もし,この内容だとすると,同ページの例1から以下のとおり反例が簡単に作れます.
の上への一対一の写像がある,ということを言われているのでしょうか.もし,この内容だとすると,同ページの例1から以下のとおり反例が簡単に作れます.
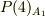 は,{e,(2 3 4),(2 4 3)} の3要素.
は,{e,(2 3 4),(2 4 3)} の3要素.
一方, 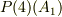 は,
は,
A 1 A 2 A 3 A 4 A 3 A 4 A 1 A 2 (1 3)(2 4)を適用 A 4 A 2 A 1 A 3 (1 4 3)を適用 A 3 A 2 A 4 A 1 (1 3 4)を適用 ...
とあり,両者に一対一対応は存在しない.
(2)home > 代数学 > 群が集合の上で働くということ
群の働き方 例5 にて
Φ g (a)=gag -1 (3) Φ g (a)=g -1 ag(4)
のように括弧数字がずれていました.(ブラウザはFirefox で確認)
(3)各トピックの上部に表示されるパンくずリストですが,一部,リンクが切れているようです.
例)固定部分群 の記事で表示されている home > 代数学 の代数学をクリックすると 404 File Not Found エラーが発生.
以上,宜しくお願いします.
Re: 軌道と固定部分群の定理
通りすがり さんのレス (2010/04/17(Sat) 17:26)
確かに(代数学 > 固定部分群)のところの指摘の証明は,次の定理のものだと思います. (代数学 > 群が集合の上で働くということ)のところの式番号については,私はそれほど気になりません. 仕様だと思います.しかし,2つの式の間にカンマ”,”入れた方が間違いがないですね.(ブラウザはIEですが,Firefoxと同じように見えます) リンクは切れてますね.