とろとろ さんの書込 (2010/04/13(Tue) 20:39)

ベクトルvの発散についてですが， 1)v=xi+yjの発散は２，2)v=-yi+xjの発散は0でいいでしょうか？ ちなみにvとiとjはベクトルです．

またvの概要をxy平面上へ描く時，1),2)ともに同じ形の図になるんですが， これは間違っていますか？ 教えてください．

Yokkun さんのレス (2010/04/13(Tue) 22:47)

発散の値は合っていると思いますが，発散の値の異なる２つのベクトル場が同じ形になるはずがありませんね？

2)について，

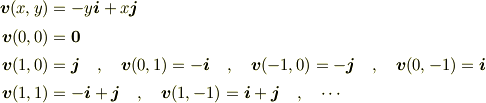
などとていねいに計算して図示してみてください．

とろとろ さんのレス (2010/04/13(Tue) 23:39)

返答ありがとうございます． この1)と2)のグラフって２変数関数のグラフなんでしょうか？？

桐 さんのレス (2010/04/14(Wed) 00:30)

横から失礼します． 同じ v だと紛らわしいので， [u](x, y) = x [i] + y [j]； [v](x, y) = - y [i] + x [j] と書きますと，明らかにベクトル [u] と [v] は x と y の２変数関数です．（どちらも z 成分はなし） ここで，ベクトルは [ ] という記号で表すことにし，[i] と [j] はそれぞれ x と y 方向の単位ベクトルを意味します．（z 方向の単位ベクトルは [k] とする） また，発散というのは， ∇ = [i]∂/∂x + [j]∂/∂y + [k]∂/∂z との内積ですから， ∇・[u] = 1 + 1 + 0 = 2； ∇・[v] = 0 + 0 + 0 = 0 となります．

Yokkun さんのレス (2010/04/14(Wed) 13:13)

ベクトル場の概要を描くのですから，x-y平面上に分布するベクトルの図を描けばよいのではないでしょうか？たとえば，x,yともに1きざみで格子点をとってその格子点における場を矢印で描き込んでいけばいいのかな，と思います．1)は原点から外向き放射状の矢印群，2)は原点周りを左回りに回転するような矢印群を描くことになります．

桐 さんのレス (2010/04/14(Wed) 17:30)

上のYokkunさんのベクトル場の説明の通りになることは，1)は発散の値が正（湧き出し）；2)は回転，つまり， ∇・[u] = 2；∇×[v] = 2 [k] となることからも確認できます．