だちわ さんの書込 (2010/03/27(Sat) 14:11)

現在，大学生です．高校以来の疑問として起電力とは？というものがあります．具体的に書くと，円周状の銅線を用意します．ここにdB/dtが一定となるような磁場をかければ，V=SdB/dtなる起電力が発生する，と高校の教科書にも載っています．さらにこの導体の一周の抵抗をRとするならば，流れる電流はI = V/Rとなることも教科書に載っています． ところが，この導体は一周回ると同じ電位に落ち着くため，起電力はこのままでは測定することが出来ません．言い方を変えて，磁場に時間変化のあるような場は，電場のrotが0にならないため，電場のスカラーポテンシャルが存在しない，と言ってもいいと思います．電位が存在しないにも関わらず定義出来る量，それが起電力です．(誘導)起電力とはつまり何でしょうか．

以下，人生の中でいろいろな人に質問した結果をつらつらと書いてみます． ・切ったときの電位差じゃないの？（定義に切るという操作を含む？） ・電位は定義出来ないんじゃなくて，無限多価なだけなので，その電位の最小の差を起電力と呼ぶ．あるいは一周回ってきた時のポテンシャルの差． ・電子に働く力そのものを表す．起電力っていうしね． ・将来，大学で電磁気学を学べばきっと分かる．（わかりませんでした！お手上げΨ）

ヒノッキー さんのレス (2010/03/29(Mon) 01:46)

こんばんはだちわさん．ヒノッキーといいます． 僕も大学生で，高校生に物理などを教えたりしています．

起電力とはなにか？ ”それは導線中に生じた電場を回路にそって一回り積分したものである．” この問題に関して，この一行で終わらせた本がありました．

”ある経路に対する電場の接線方向成分の積分が電位差となる”ことは 大学で授業を受けていれば知っていることだと思います． なのでおそらく，だちわさんは上記の一行だけでは納得しないでしょう． なぜ”一周分”の積分を起電力と考えられるのか？ というふうに切り返してくると思います．

これについては僕もよくわかっていないので， 憶測となってしまいますが……

すみません，考えていたことがちょっとまとまらなく なってきました．すこし時間がかかると思います．

とりあえず，上述の問題の置き換えには納得していただけるでしょうか？

治具工房 さんのレス (2010/03/31(Wed) 18:26)

電池（単三乾電池3個)抵抗（10Ω1Ｗカーボン抵抗3本)を用意し， 電池→抵抗→電池 ↑↓ 抵抗抵抗 ↑↓

電池

と回路が閉じる様に，直列に交互に円環状に接続する．

この回路の電圧をテスターで測定すると， 1.5V 0V 電池→抵抗→電池 GND↑ ↓1.5V 抵抗抵抗 1.5V↑↓0V

電池

とテスターに表示されることでしょう．(私はこの実験をしたことがありません．)

質問の【円周状の銅線が一周回って】閉じている場合は，思考実験として， 沢山の微少電圧の電池と抵抗が直列に交互に円環状に接続されている状態， あるいは，電池と抵抗が混然一体となっている状態と考えたら・・・よいでしょう．

働いて給料は出るが，社会保険料・寮費・何だかんだと引かれて手取り零の象．

治具工房 さんのレス (2010/04/01(Thu) 21:32)

?上記の思考実験の説明は舌足らずでした． 細い銅リングの各箇所での起電力÷抵抗＝一定の条件が必要でした． 各箇所での抵抗は普通は一定なので，各箇所での起電力も又一定の想定でした． この場合，リング上の電位は全て一定で，電位差が全て零なのに電流が流れています． 電位差が零なのに電流が流れるのは奇妙ですが，上記の思考実験から単純に納得できるはずです．

?交流発電の原理の説明によく使われる構造では， 磁界の中で串焼き様に銅リングを回転させると，リング上の各箇所での起電力は一定でない． 各箇所での抵抗は普通は一定なので，各箇所での起電力÷抵抗は一定ではなくなる． この場合，リング上の電位は一定でなく，電位差が正もあれば負もある一周のはずなのに， 電流はリング上を一定方向に流れているはずです．（交流電流であるが，ある瞬間の観察ではの話) 電位差に逆らって電流が流れるのは奇妙ですが，それも起こり得ると私は主張します．

ヒノッキー さんのレス (2010/04/02(Fri) 01:54)

だいぶ，考えがまとまったので帰ってきました．

こんばんは治具工房さん． 治具工房さんの考え方につい２，３疑問に思うところはあるのですが， とりあえず，だちわさんの返答を待ってからにしたいと思います． ですので，治具工房さんの話には触れずに自分の考えの続きを 書いていきます．

前回， ”誘導起電力は導線中に生じた電場を回路にそって一回り積分したものである．” というように説明したものがあると言いました． 電場の足し合わせが電位差というのは，大学生ならばおそらく納得して いただけると思い，なぜ一周分の積分だけで事足りるのか？ ということへの説明をしようと思っていました． しかし，やはり推測の域をでないので，疑問点やおかしい点があれば 教えてください．

とりあえず自然現象として， 磁場がかかっている⇒電場が円周上に発生する⇒電子が電場によって動き， 電流が発生する．

ということはイメージにあると思います． しかし，通常電場がかかっていればどこまでも電子が加速するはずで， 電位は無限となるはずでは？ これが第一の疑問でしょう． これに対し，現実は一定の電流が流れていることを示します． つまり，電場が電子を運ぶ力に対する抵抗力があり， この二力が釣り合っている，ということを示唆していると思います．

今回考えている電位差とは，この釣り合った状態を考えているのでは ないでしょうか？ とにかく一定の電流が流れることは分かる． では，抵抗や電位差はどこを取れば考えやすいか？ おそらく，どこを始点とし，どこを終点としてもよかったのだと思います．

今回，電位差（V=Ed）も抵抗（R=ρd/S）も始点から終点までの距離に比例して 大きくなるので，V=IRより，両辺からdが落ち，距離に関係なく 電流は一定であることがいえます．

なので，あとはどこを取ることが最も考えやすいか？ということになり， 一周分，となったのではないでしょうか？

治具工房 さんのレス (2010/04/03(Sat) 11:13)

?だちわ?さんの質問で 「この導体は一周回ると同じ電位に落ち着くため」 とありましたので，

導体は一周して短絡していると解釈しました．指環の様な細い銅環で考えました． この解釈が誤りならば，すなわち短絡していない場合は同じ電位に落ち着くとは限らず， 端が開いた銅環あるいは適正な負荷が接続された銅環の両端では， ?ヒノッキー?さんの「回路にそって一回り積分」に比例した電位差が観測されます．

縁が金メッキの茶碗を電子レンジに入れると焼き切れると聞きますので， これはに似て面白いテーマかなと，早ガッテンが過ぎた様です．

ヒノッキー さんのレス (2010/04/04(Sun) 15:06)

「回路に沿って一回り積分」は，抵抗による電圧降下を無視したとき， 一周分でどれほどの電位差が生じるか？ということを示しているのだと 思います． そのため，実際には抵抗による電圧降下があるので，この状態で この電位差は測れません．

しかし，治具工房さんが示したように端を開いてそこに 抵抗をつければ，確かに電位差を測定することはできると思います．

僕が考えたことと，治具工房さんがおっしゃっていることは ほとんど似ていますが，治具工房さんの「電位」は 抵抗も含めて考えたもので，僕の言う電位差は抵抗を除いて 考えたもの． そしてだちわさんが疑問に思っている，電位差０なのに起電力が生じる，とは 電位差０⇒治具工房さん 起電力が生じる⇒僕 という二つの結論を混同してしまったのではないでしょうか？

教科書などで求められる起電力とは，抵抗による電圧降下を 考えないので，僕の考え方で正しいと思います．

P.S. 治具工房さんの考えたことは単純な電池に抵抗をつなげただけの回路でも成立します． テスターの二端子を全く同じ部分につける行為と同じことです． その部分の電位は明らかに０なので，”一周まわれば”同じ電位です． 大事なのは，抵抗による電圧降下を考えないことではないでしょうか？

だちわ さんのレス (2010/04/06(Tue) 07:00)

返答が遅くなりました．いろいろと回答していただいてありがとうございます． ヒノッキーさんへ． 「電場の足し合わせが電位である」これを当たり前のように書いていますが， 基本的に疑問はここなのです．どこの教科書の何ページに「電場の足し合わせが 電位である」と書かれているでしょうか．教科書には一般に，ベクトル場Fの 回転が0であるような場合，∇V=Fとなるような関数Vが存在し，それを（符号を 変えて）ポテンシャルと呼ぶ，と書かれています．その上で，電位は電場の スカラーポテンシャルだと定義されていることが大半です． 起電力は電位差でしょうか．誘導起電力は磁場の変化を伴っています．このような 場では電位は定義出来ないか，多値関数とされるでしょう．この世界で電位差は 定義出来ますか？とすると，誘導起電力を電位差で定義するのはおそらく間違って います．ちなみに電場は「存在しません」．

治具工房さんへ． よく回路理論の分散定数なんかでは，成分を細かく切って，その極限を求めて 集中回路定数として等価回路を書いたりします．当然，今回の場合でも， チビチビ電池とチビチビ抵抗を交互に配置した上で，極限をとれば，集中回路定数 としての起電力Vと電圧降下Vが一致するようなモデルになります． ポイントは応用上の話ではなく，もっと原理的な話なのです． 当然，私自身，起電力を求めるくらいは出来ます．

批判的になってしまいましたが，回答には感謝しています．

だちわ さんのレス (2010/04/06(Tue) 07:21)

すみません．電場は存在します． 微小区間dsで電子が力Fを受けたとすると，電子が受け取るエネルギーはFdsの はずです．ところで「仮想的な電位差」を考えると，edVだけエネルギーを受け 取っています．そこで仮想的な電位差は dV = Fds/eと定義するのがよいでしょう． あとは適当な区間で積分をした値 V=∫(F/e)ds を起電力と呼ぼうではないか！という話は全然理解出来るんですが， 性格上，「仮想的な電位差」なんてものも納得できないし，適当な区間なんて 言われても困ってしまうのです．

ちなみにこれは ・電子に働く力そのものを表す．起電力っていうしね． に対応した理解です．

mNeji さんのレス (2010/04/06(Tue) 21:49)

だちわさん，横から失礼します．

＞すみません．電場は存在します． ＞微小区間dsで電子が力Fを受けたとすると，電子が受け取るエネルギーはFdsの ＞はずです．ところで「仮想的な電位差」を考えると，edVだけエネルギーを受け ＞取っています．そこで仮想的な電位差は dV = Fds/eと定義するのがよいでしょう． ＞あとは適当な区間で積分をした値 ＞V=∫(F/e)ds ＞を起電力と呼ぼうではないか！という話は全然理解出来るんですが，

このご発言は，まさにその通りではないでしょうか．この論議では「仮想的な電位差」を仮定していないのではないでしょうか．少なくとも；

「閉回路を一周する間に，電場から受ける力が電子にする仕事を起電力と呼ぼう」

と言っていると解釈するので宜しいのではないでしょうか．ただし，通常のポテンシャルのように，保存力でない「その電場の回転がゼロでない」という点には注意が必要だと思います．

＞・電子に働く力そのものを表す．起電力っていうしね．

私は，大学１年生のころ，この「起電力」を「電場を起こす"力"」と無意識に読んでしまって混乱した記憶が朧げにあります．

＞性格上，「仮想的な電位差」なんてものも納得できないし，適当な区間なんて 言われても困ってしまうのです．

私は，高校生のころ『「重力ポテンシャル」を説明するときに重力に逆らって「準静的な力」を加えて遠方から考察点までにする仕事』といった説明を受けて『？？？？？？？？？？？』という悩みを抱えた記憶がハッキリありました．

なんとなく さんのレス (2010/04/06(Tue) 23:34)

だちわさん，初めまして．

起電力は英語ではEMF(Electromotive force)ですが，まさに電流を流そうとする力（の起因）であると考えています．ここで背景に導体が存在します．ある場合はそれは電位（差）として現われ，そうでないこともあります．導体では通常同電位ですが正負の電荷が釣り合っているためであり，時間的に一定でも空間的に偏れば電位(差）が生じますね．では電流が流れているときはどうかというと，電荷の量が釣り合っていれば電場は生じない（キャンセルする）と言えます．DivD=ρより（静）電場は電荷によるからですが，磁場が生じます．また，磁場変化がある場合は，その電磁誘導による電場，RotE=-∂B/∂tより，E=-∂A/∂tが生じるのでベクトルポテンシャルが存在（し時間変化）することにより電場が生じるとも言えます．静的な場，定常（動的でも時間的に一様な）場，時間的に変化する場，を踏まえて定義を評価する必要があると思います． したがって，起電力は電位で定義されるというより，電位で定義される（できる）ような回路があれば電位差で，そうでない場合はそれと等価である電流駆動力（例えば電磁誘導）を示すと考えればよいと思います． 円環電流，とくに完全導体（抵抗０）であれば，電位差は無いですが電流が流れ続けることは超電導で周知ですが，その初期駆動は電磁誘導で行うこともあるようです．まさに起電力による電流の発生です． つまり起電力とは電場の発生により電子に働き（導体に）電流を発生させる力，と言えるのではないでしょうか． 相対論的に見れば，電場と磁場の役割が入れ替わっているように見えますね．

ヒノッキー さんのレス (2010/04/07(Wed) 00:24)

>「電場の足し合わせが電位である」これを当たり前のように書いていますが， 基本的に疑問はここなのです．

これは僕なりの説明になりますが，

F=qEより，電場とは，「単位電荷を動かすための力」と考えることが できるはずです．そうすれば， Edrは「単位電荷を動かすための力が，微小距離drだけ電荷を動かした際に 必要なエネルギー」と言え，これを求めたい経路内で足し合わせたものは， 「始点から終点までに必要なエネルギー」となり， これをポテンシャル（電位差）と呼ぶのだと考えています．

一応高校物理の内容で説明すれば，こうなると思います． だちわさんの意見で出てくる部分もありますね． あと電位，電位差の違いですが，基準値（無限遠を0Vとする，など）を 取っているとき，その基準値からどれほど高いのかを電位． 単純に2地点での電位の違いを電位差と考えています． たしか，こういう定義だったと思うのですが，どうでしょうか？

＞ポイントは応用上の話ではなく，もっと原理的な話なのです．

磁場により円環上に電場が発生し，発生した電場により電子が加速される． ただ，ある一定の速度になると抵抗力と電場による力が釣り合い， その速度で安定する．⇒この安定した時の電流を考えている．

僕は原理的にはこのようなものだと考えています． 力学のような話になりますが，こちらから考えたほうが イメージがつきやすいと思います． あと，「仮想的な電位差」とはどういう意味でしょうか？ 今回の場合，確かに電子を動かしている電場が存在するので， 電位差（起電力）はあるはずです．ただ，それと同じエネルギーだけ 抵抗にとられてしまい，電位差がないように見えるだけだと考えています．

実際の電位差をどこでとるか？などはmNejiさん（お久しぶりです）からも 意見が出ていますが， ・現実的に最も抵抗を測りやすい区間はどこか？ ・実際に治具工房さんが例に出していたように，円環を開いて外部に抵抗を つなげると，電位差はどうなるか？ ということを考えてみれば，一周分と取るのは自然ではないでしょうか？

なんとなくさんへ 超電導状態では確かオームの法則が破たんするので， 今回の話ではあまり挙げないほうが混乱が少なくて済むと思います…… 超電導状態のことを挙げられると，上の説明で，電流が無限に加速される ことになっちゃうので……

なんとなく さんのレス (2010/04/07(Wed) 10:59)

ヒノッキーさん

了解．ミクロな物理的描像は御説明でほぼ良いと思います． だちわさんがそれで納得されるなら，超電導を持ち出す必要はないです． ただ， >電流(電子）が無限に加速される という言葉に表れているように，加速する（電流が０から生じる，あるいは増減する）には電場が必要ですが，電流が流れていても必ずしも外部電場（電位差）は必要でない，ということを視野に入れておかねば説明が足りない気がします．だちわさんの基本的疑問はその辺りにある気がするのですが．

ヒノッキー さんのレス (2010/04/07(Wed) 12:48)

>加速する（電流が０から生じる，あるいは増減する）には電場が必要ですが，電流が流れていても必ずしも外部電場（電位差）は必要でない，ということを視野に入れておかねば説明が足りない気がします．

これはつまり，電子銃で撃ちだされた，電子の運動などでしょうか？ 確かに，電流が流れるているのに電場が必要なわけでは ありませんね．

これについても力学的な説明をするならば， 「力を加えなければ，電子は等速直線運動を続ける」ため， 電場がない場合でも，電子銃のように最初電場によって加速され， 「初速がついた状態」で撃ちだされた電子は等速直線運動を行い， それを電流と見ることができる．と考えればよいと思います．

いつも考えている状態ではほとんどが， 「力が加わっていない」あるいは「抵抗による減速しかない」状態を 考慮するだけでよかったのだろうと思いますが， （おそらくこちらの方が実例が少ないかと思いますが） 今回は，「加速と減速の力が同時にはたらいている」ことに 注意する必要があります． 電子銃などの作る電流は「力が働いていないために等速で動く」で， 今回の話は「力が釣り合っているために等速で動く」という 違いがあります．

だちわ さんのレス (2010/04/07(Wed) 20:36)

ありがとうございます． ヒノッキーさんへ． >F=qEより，電場とは，「単位電荷を動かすための力」と考えることが >できるはずです．そうすれば， ここはヒノッキーさんがおそらく「勘違い」されていると思うので， 教科書的に解説します．電場や磁場などの話ではなく，もっと一般の 「ベクトル場」というものを考えます．ベクトル場は，例えば3次元空間上で 一点を定めるとx,y,z方向の成分を持つベクトルを一つ定めるような関数の ことを指します．ところで，ベクトル場に対して，特に特別な場合には 3次元空間上の一点を指定すると，ある関数の勾配としてベクトル場を 表すことが出来ます．その場合にその関数を（符号を変えて）ポテンシャルと 呼ぼうということになっています．また，そういう場（層状ベクトル場といいます） では特にベクトルの線積分が経路によらず一定になるという性質を持ちます． 力学では保存力と呼ばれるものですよね． だから，説明が逆なのです．静電場がなく磁場が時間変化するような場における 電場は典型的な管状ベクトル場なので，当然ポテンシャルは存在しないという ことになります．電位は定義が電場のポテンシャルでしたから，電位は存在しない． 電位差はしたがって存在しない（未定義）となるのが自然です． 繰り返しになってしまいますが，起電力が電位差であると定義すれば 両端の短絡したコイルの起電力は「未定義」となります．

mNejiさん，なんとなくさんへ． 確かに，それが自然な定義ですね． ありがとうございました．

ヒノッキー さんのレス (2010/04/08(Thu) 01:16)

なるほど…… 確かに円状のベクトル場としてみれば一周後の高低差はあってはならず， よってポテンシャル（電位差）はない，となりますね． そこから，mNejiさんやだちわさんの「仮想的な電位差」という 言葉がでてきたわけですね．よくわかりました．

しかし，納得はできません． なぜ教科書などで「仮想的な電位差」という記述をしたり， 言及したりしないのでしょうか？ それは，円環中の電位差の存在が事実であるからだと思います．

もしかしたら，「ベクトル場で考える」ということ そのものに問題があるのではないでしょうか？

ここからは推論です．

上記のベクトル場で言うポテンシャルとは やはり一般的な総称であって，電位差とはなんら関係のない言葉では ないでしょうか？（修正：大間違いです）

ベクトル場のポテンシャルとは，そのベクトルの正体が電場なら， 「電場によるエネルギーの流出」という値を求めていて， もしもそれが保存力場でない場合， 「電場によるエネルギーの流出」が存在するということを （電磁波など？） 求めているのではないでしょうか？（修正：大間違いです．忘れてください．）

一方，電磁気学上でのポテンシャルとは，，（修正：起電力を求める際は） 「電子が電場からどれほどのエネルギーを受け取ったか？」のはずです．

ベクトル場でのポテンシャルの考え方は，その経路に「電子」を置かずに 考えているはずです．これは電流を考える上でおかしいことのはずで， やはり「仮想的な電位差」というものは存在しないと思います．

多くの人がこの二つ（電位を求めるときの考え方と 起電力を求めるときの考え方）を同じように取り扱ったから今回のような おかしな事態が生じているのではないでしょうか？ （修正：僕はこの二つは区別できていましたが，二つとも電位差と呼んでいたことに問題があったようです．）

正しく現象を説明できていないツールを考えるとき， 現象とツールどちらを信頼するか？ それは現象ではないでしょうか？ ですので，ツールを合っているとして「仮想的な電位差」を持ち出すのは 事実を捻じ曲げる，非常に危険な行為だと思います． （修正：僕の中での電位の定義がおかしかったので， こんなことを書いてしまいました．）

yama さんのレス (2010/04/08(Thu) 01:38)

横から失礼します．

電場はベクトル場であって，「単位電荷を動かすための力」はベクトルなので，電場を「単位電荷を動かすための力」と考えることは厳密に言えば正しくありませんね． 正確には，「単位電荷を動かすための力」が空間の各点（および時間）の関数として定まるとき，その空間（ベクトル場）が電場であるとすべきでしょう． しかし一般的には，「単位電荷を動かすための力」自体も電場と呼ぶことも多いようです．区別する必要があるときは，後者を電場ベクトルと呼ぶことがありますが，多くの場合は単に電場と呼ばれます．

だちわさんが述べられている通り，変動する磁場が存在する場合は電位は定義できません．勾配の符号を変えたものが電場になるようなスカラー場が存在すればそのスカラーポテンシャルを電位と考えることができますが，そのようなスカラー場が存在しないからです． この場合でも，スカラー場に加えてベクトル場（ベクトルポテンシャルの場）も用いて

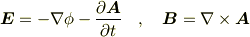
と表すことはできます．しかしゲージ不変性のため や 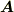は一意的に決まらないのでこの場合のスカラーポテンシャル を電位と考えるのは不適切でしょう．

次に起電力についてですが，この用語はあまり適切ではないように思います．起電力というと，電流を生じる力であると考えたくなりますが，力自体ではなく，その力のする（単位電荷当たりの）仕事を起電力というようです． これは結局だちわさんが書かれているように V=∫(F/e)ds になります．この場合の力としては非電磁的な力も含みます．例えば電池の起電力は化学的な力によるものです．もっとも微視的に見れば化学的な力も結局は電磁力に帰着されますが・・・． 円周状の銅線に生じる誘導起電力の場合は，電荷に働くのは誘導電場による力なので

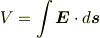
となります． 回路全体の起電力は円周を一周する積分になります．それが単位時間当たりの磁束の変化に等しくなることはご承知のここと思います． また円周の一部分だけの積分値をその部分の起電力と考えることができます． 場合によってはこの部分的な起電力をあたかも電位差のように見なすことができるので，これをだちわさんは「仮想的な電位差」と呼ばれたのでしょう． しかしもちろんこれは真の意味での電位差ではありません． そもそも電位自体が定義できないわけですが，それはともかくとしても，真の電位差は一周分足し合わせると０になりますが，部分的な起電力を一周分足し合わせたものは全体の起電力になるからです． なお銅線を円周状にn回巻いた回路では，回路全体の起電力は，円周をn周する積分になるので１回巻きの場合のn倍になることもご承知のことと思います．

ヒノッキー さんのレス (2010/04/08(Thu) 02:06)

こんばんわyamaさん． yamaさんの文を見てると，考えが変わってきました．

僕は，電位差＝エネルギーという考えが頭を離れず， 変なことを書いていたようです．

電位とは確かに電場の勾配のことです．

＞一方，電磁気学上でのポテンシャルとは

ここは，かなりおかしな事を話していますね． すみません．僕が電位差，電位と呼んでいるものを すべて起電力と読み換えたら，上手くいくと思います．

電場の勾配による電位と，電子が得たエネルギー． この二つを僕はどちらも電位と語ってしまいました． これからは電位差という言葉を使うときは注意しなければ いけませんね．

だちわさんが「仮想的な電位差」と呼んだもの， そして僕が間違えて電位差，電位と呼んでいたもの， それこそが起電力のことだっていうことですね． これならば，教科書で「仮想的な電位差」という単語が 出てこないのも分かります．

やはり，「仮想的な電位差」という言い方には抵抗があります． しかしそれは，僕が今まで電位差（電子が電場から受け取ったエネルギー）と 呼んでいたものと全く同じものを指していたからです．

＜僕なりの結論＞ 起電力＝電子が電場から受け取ったエネルギーのこと． 電位差＝電場の勾配によるポテンシャルエネルギー

ということですね． どうやら，とんだ勘違いをしていたようで すみませんでした．

mNeji さんのレス (2010/04/08(Thu) 11:50)

ヒノッキーさん，

＞やはり，「仮想的な電位差」という言い方には抵抗があります．

わたしも「仮想的な」という記述の意味が分りません．

以前，なんとなくさんが， ＞起電力は英語ではEMF(Electromotive force)ですが，まさに電流を流そうとする力（の起因）であると考えています．

と書かれましたが，私の心の中では「EMF」の代わりに，「EMP(Electro Motive Potential)」と呼びたいと思うほどです．さらに具体的には，電池の場合，「Electro Chemical Potential」と呼び，電磁誘導の場合「Electromagnetic induced Potenntial」とでも呼べば，紛らわしく無かったのだと思います(笑)．

何れの場合も，出来た電場は，通常の導体中の可動電荷(普通，電子ですが)に作用して「實の仕事」をしますが，その力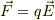， は，金属格子から逆方向の力を受けて事実上，平衡しているので，可動電荷は金属格子の振動エナジとしてエナジの散逸をしてしまうのではないでしょうか．

そう考えると，何を持って「仮想的な」と言うのかを知りたい所です．

ガス さんのレス (2010/04/08(Thu) 17:08)

講談社なっとくする演習・電磁気学後藤尚久著の，プロローグに 似たようなことが，書いてあります．