なす さんの書込 (2010/03/21(Sun) 20:39)

初めて質問させていただきます． 電磁場の量子化でたとえばFeynmanゲージを使うとスカラー光子が現れますが， これがクーロン力の伝達と関係している，というのはどこから出てきているのでしょうか．

「場の量子論」(中西襄培風館)では 「スカラー光子のほうは物理的状態であるが，ノルムがゼロということのために 確率解釈に従えば決して観測にかからない．これはCoulomb力の量子が決して 観測されないことに対応する．つまりCoulomb力はスカラー光子によって 近接作用として記述されるわけである」 とあり，ノルムがゼロである→したがって観測されないの理由は 説明されていますが， 「Coulomb力がスカラー光子によって近接作用として記述される」 となる理由が判らないのです．

ハミルトニアンの表式を見ても，スカラー光子部分は縦波光子と一緒に 消えてしまう項ですので，スカラー光子部分のエネルギーが クーロンポテンシャルによるエネルギーの式になるわけでもなさそうですし…

nabeyang さんのレス (2010/03/21(Sun) 21:44)

フォトン・プロパゲータの|99b8b34787e9ec61ed6bce4003f34910|成分がクーロン力と関連するとおもいますが， この部分がスカラー・モードから来るってことだと思います．もうちょっと， 丁寧に考えないと，これで良いか分からないですが．

B場とゲージ場のスカラー・モードの関係から解釈できるか考えていますが， -A_{0}はB場でなく，その共役運動量なので，こじ付けっぽい(誰もが納得するとは限らない)解釈なのかもしれません．とりあえず，ゲージ場の0成分をもはや座標ではなく，B場の共役運動量として考えて，クーロン力の計算をやり直してみたら，おおよそ言っていることが理解できるのではないかと思っています．

追加------------------

定義に戻ってみたら，ゲージ場の0成分には縦波モード，スカラーモードしか含んでいません．そして，いずれも非物理的モードで観測にはかかりません．そして，クーロン力として効くのはこのA_0成分です(プロパゲータの00成分なので)． 中西さんの解釈と完璧整合するか分かりませんが，これがクーロン力の働くに粒子間を飛び交うゲージ場のモードは観測不可能なモードしか含まないという結論としては一致します．

なす さんのレス (2010/03/22(Mon) 10:43)

回答ありがとうございます． 今朝図書館に行って「素粒子物理学の基礎1」(朝倉書店)で さらに調べたところ， 「フォトンが中間状態に現れるときは通常次のように保存カレントに はさまれていることに着目する． （略） (4.75)（引用註：保存カレントで偏極の和を挟んで和をとった式）は 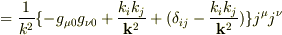= 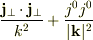(略)」

最初の式の第1項がスカラー，第2項が縦波，第3項が横波成分であり， この第1項と第2項が2番目の式の第2項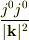， ， 最初の式の第3項が2番目の式の第1項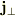（ は保存カレントのうち に直角な成分）になり， この 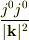がクーロンポテンシャルの寄与ということらしい， というところまではたどり着きました． 後はここからクーロンポテンシャルにどうやってつなげるか…というところです．

>ゲージ場の0成分には縦波モード，スカラーモードしか含んでいません． >そして，いずれも非物理的モードで観測にはかかりません． >そして，クーロン力として効くのはこの 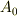成分

上の式を追ってみたところでも，スカラー成分単体ではなく， 縦波成分とスカラー成分の両方からクーロンポテンシャルの項が出てきていると いうのが正解のようですね． #このあたり，本によってはクーロン力＝スカラー光子で伝達，という記述と， スカラー光子と縦光子両方で伝達という記述の両方があるようです． （「量子論の発展史」とか）

nabeyang さんのレス (2010/03/23(Tue) 10:48)

e + e -> e + e の散乱振幅とポテンシャルを関係付けることはできますか？それの非相対論的極限をとると，クーロン力とフォトン・プロパゲータの00成分とが対応することが理解できるはずです．Peskinとかあったら，4.8のthe coulomb potentialのところで取り扱っているので，調べてみてください．

なす さんのレス (2010/03/23(Tue) 21:17)

>e + e -> e + e の散乱振幅とポテンシャルを関係付けることはできますか？ この辺は「素粒子〜」に記述がないので，どうしようかと思っていたところです． 直感的には1/rを波数kでフーリエ変換すると 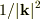になるのでまあOKかな，と甘いことを考えていたのですが．

>Peskinとかあったら，4.8のthe coulomb potentialのところで >取り扱っているので，調べてみてください． アドバイスありがとうございます． Peskinは…近所の図書館にはないようでしたが，持ってて損はなさそうなので 買ってみようかと思います．

なんとなく さんのレス (2010/03/23(Tue) 22:26)

私も良く分からないので興味を持って拝見しています．

それで，いくつか疑問に思ったことを書かせてもらいたいのですが，あまりに昔の時代の記憶ですので，的外れはご容赦を．

一部既出ですが，中西の本によれば縦光子（非物理的状態，ノルム不正定値），スカラー（物理的状態，ノルム０），・横波光子（物理的状態，ノルム正定値），と明記されていますが，スカラーを非物理的状態とするのは歴史的なものか，或いは現代でも解釈の問題でしょうか（ゲージの問題では無さそうです）．ここで物理的状態とは確率解釈（０含む）から言うようですね．

なすさんが次に書かれたカレントによる表記は，単純にそのまま見ればi〜j(1〜3)，μ，ν(0〜3)の規約により， この第1項と第2項が2番目の式の第2項→この第1項が2番目の式の第2項 の気がします． 第一の式は，結局，δijしか残らず，空間部分のみとなるからです． とすると，やはりスカラー光子がクーロン力を担うと見て良い気がします．

nabeyang さんのレス (2010/03/24(Wed) 04:00)

なすさん， >>e + e -> e + e の散乱振幅とポテンシャルを関係付けることはできますか？ >この辺は「素粒子〜」に記述がないので，どうしようかと思っていたところです． >直感的には1/rを波数kでフーリエ変換するとになるのでまあOKかな，と甘いことを考>えていたのですが．

とりあえず，量子力学の散乱理論（ボルン近似）は理解していますか？それを理解していれば，分かるとおもいます．とりあえず，今計算しているものと，ポテンシャルとの関係性が明らかにできない限り，クーロン力がどうとか，そういったことは理解できないことになります．

このことについて，まず理解しないと，先に進めないんじゃないかと思います．

なす さんのレス (2010/03/24(Wed) 06:51)

なんとなくさん ＞なすさんが次に書かれたカレントによる表記は，単純にそのまま見れば （略） ＞とすると，やはりスカラー光子がクーロン力を担うと見て良い気がします．

δijしか残らないのは一見その通りなんですが， 無理やりkikj/k^2とδij-kikj/k^2に分離して変形していくと 次の式になったのでOKだと思っていたのですが．

nabeyangさん ＞とりあえず，量子力学の散乱理論（ボルン近似）は理解していますか？

前に出てきたなあ，という程度ですね…

＞今計算しているものと，ポテンシャルとの関係性が明らかにできない限り， ＞クーロン力がどうとか，そういったことは理解できないことになります． ＞このことについて，まず理解しないと，先に進めないんじゃないかと思います．

どうやら素人（大学は機械系工学部でした）にはかなり先が長いようです． やはり5合目まで車で上るようなのはいけませんね．

もともとは親戚の子供に聞かれた 「ブラックホールからなぜ重力は出てこられるのか」 という質問を考えていまして，いろいろ調べてみると， →ブラックホールが電荷を持ってる場合はクーロン力も出てこられる →クーロン力伝えてるのは光子じゃないのか →それは仮想光子だから光速の制限を受けない →じゃあ静的な重力も仮想重力子が伝えているから出てくるのか →クーロン力は出てこられるが普通の電磁波(?)が出て来られないのであれば， 荷電ブラックホールに逆符号の電荷を投げ込んでいくとそれまで出てきていた クーロン力はどうなるのか

といろいろな疑問が湧いてきまして，その辺りを追ってみようと思っていたわけです． 式を追わないで結果だけを知って語るのはなんとなく気持ち悪いので． #まあ，先は長そうです．

nabeyang さんのレス (2010/03/24(Wed) 10:08)

>＞とりあえず，量子力学の散乱理論（ボルン近似）は理解していますか？

>前に出てきたなあ，という程度ですね…

そうですか，でも一方で，場の理論で散乱振幅は計算できるんですよね(Feynman ruleを作って)．落ち着いて，復習してみたら，クーロン力の話は理解できると思います．ブラックホールの話はまた別で，量子論まで突っ込む必要があるのかって疑問があります．量子論になると，ホーキング輻射とかその辺の話になるんだと思いますけど，ぼくは勉強したことないです．

なんとなく さんのレス (2010/03/24(Wed) 11:51)

なすさん．

これはまた，えらい問題を抱えたものですね．大筋はnabeyangさんの言われる通りと思いますけど．

ただ，ブラックホールから重力（やクーロン力）が“出てくる”という表現はやはり変な気がします．シュバルツシルト半径はブラックホールの本質である特異点ではなく，そこでは通常の時空間と連続につながっているので，観測上の問題ではないかと思われます．例えば遠方観測者にはそこへ落ち込む物体は半径で張りついたように見え，やがて赤外変位で見えなくなると思われますが，あたかもそこで重力が無くなったように見えるわけです．しかし，物体の座標系では通常に重力を受け通過するので，結局ブラックホールはその分質量増加し，重力も大きくなるでしょう．電荷を持った粒子も同じように振る舞うでしょうから，その分全体電荷が増しますね．反対符号なら減少するだけです．つまり，周囲空間に作る電場がその内側の総電荷によると言うガウスの法則に従うだけですね．特異点でどうなるかは，神のみぞ知る，でしょう． もっとも，相対論的に電磁場を含めて近傍空間を重力場と同じ立場で理解するにはカルツァクライン理論（の拡張）が必要かもしれませんが，もちろん，まだ成功していませんし．

nabeyangさん

メラー散乱からクーロンポテンシャルとの比較をせよ，ということなのですが，何かヒントがありますでしょうか．一応散乱理論は専門だったのですが，恥ずかしながら分かりません．理屈では通常の計算を座標表示に置き換えてやればいいような気もしますが酷いことになりそうです．光学定理か或いは何か簡便法がありますでしょうか．ご教示願えれば幸いです．

なす さんのレス (2010/03/24(Wed) 12:34)

nabeyangさん>でも一方で，場の理論で散乱振幅は計算できるんですよね

ステップは（とりあえず）踏めるがなぜそのステップなのかは あまりよくわかっていない程度の踊り子さんですので あまり期待しないでください；；今後いろいろと復習してみます．

なんとなくさん＞これはまた，えらい問題を抱えたものですね． 子供の質問は侮れませんよねえ．

＞ブラックホールはその分質量増加し，重力も大きくなるでしょう． ＞周囲空間に作る電場がその内側の総電荷によると言うガウスの法則に従うだけ

確かにそう考えれば不思議な点は特にありませんね． 情報が出てきているわけではないから問題ない，ということでしょうか． 外からの電荷の投げ込み具合を時間的に変化させると周辺の電場も時間的に 変化すると思いますが，これはもともと外にあった情報なので問題ない…のでしょうか？

なんとなく さんのレス (2010/03/24(Wed) 22:40)

なすさん

>外からの電荷の投げ込み具合を時間的に変化させると周辺の電場も時間的に 変化すると思いますが，これはもともと外にあった情報なので問題ない…のでしょうか？

電荷を投げ込む間に周囲の電場はそれなりに変化し，シュバルツシルト半径を越えても連続的に変化するだけではないでしょうか． それで気になったのですが，仮想光子だから光速の制限を受けない，もおかしい気がします．電荷の運動による電場の変化は遅延ポテンシャルとして周囲に伝わり，やはり光速の制限を受けると思います．

なす さんのレス (2010/03/25(Thu) 06:45)

なんとなくさん＞仮想光子だから光速の制限を受けない，もおかしい気がします

すみません，これは検索したらいくつか出てきた説明であって， 自分で理解して主張している話ではありません． この辺はネット検索だと子引き孫引きの上トンデモな説明も多いので， 自分で調べてみようと思ったのも今回の動機です．

nabeyang さんのレス (2010/03/25(Thu) 13:59)

なんとなくさん> >メラー散乱からクーロンポテンシャルとの比較をせよ，ということなのですが，何か>ヒントがありますでしょうか．一応散乱理論は専門だったのですが，恥ずかしながら>分かりません．理屈では通常の計算を座標表示に置き換えてやればいいような気もし>ますが酷いことになりそうです．光学定理か或いは何か簡便法がありますでしょう>か．ご教示願えれば幸いです．

量子力学の散乱振幅って，ポテンシャルの言葉で書けたはずです．それと，場の理論の散乱振幅は，同じ量を計算しているので，一致するはずですよね．このようにして，"有効ポテンシャル"を場の理論から計算することができます（だから，オールオーダーで計算すると，微細構造定数は裸のパラメータでなく，繰りこまれた微細構造定数になります．）．このとき，場の理論の基本的な自由度が場だったのに対し，量子力学の自由度は粒子の位置に置き換わります．

スカラー・モードとかって場の理論の言葉なので，それでクーロン・ポテンシャルを解釈するならば，場の理論で，2つの電子が衝突する(非相対論的には，荷電粒子間にはクーロン力が働く)ような過程を計算すれば良いという感じです．同じことを書いている気もするので，答えになっているか不安です．

(イメージとしては，帯電球が止まったフレームを取って，それに向けて電子を飛ばします．ある程度のところで，飛んでいる電子はコツンと相互作用を起こして運動方向を変えます．その原因は，ターゲットである帯電球の中の電子から出たフォトンというようなことだと思っています．これを非相対論的かつ古典論で考えると，ラザフォードの問題のような設定になる気がしませんか？)

なんとなく さんのレス (2010/03/25(Thu) 17:31)

>nabeyangさん

仰ることはその通りだと思います．知りたいのは，有効ポテンシャルの具体的な求め方なのです．つまり場の理論からクーロンポテンシャル〜∝r^(-n)，出来れば，n=1も導出する方法です．勿論，手計算で．散乱理論では通常，力の働き方は問題にしないで，入射波と散乱波への遷移確率から微分断面積を求める（としか私の知識は無い）ので，途中のダイナミクスは消えてしまいます．これは上記有効ポテンシャル空間の積分によって位置座標がなくなることに対応しています．実際，結果は（球対称なので当たり前ですが）角度分布のみが問題となります．勿論，結果を比較して，推定することはできますが，逆問題としてポテンシャルを決定することは一般に不可能かさらに困難でしょう． そこで，素過程である場の理論から直接，導く方法があるのではないか，と思ったわけです．πオンの交換が湯川型になることの証明があった気がするのですが，そのイメージです．もっとも，さらに基本的な勘違いをしているかも知れませんが．

蛇足ですが，最後に書かれたコメントは井戸型ポテンシャルとして有効ポテンシャルを決定出来そうですが，ポテンシャルが定数となるプリミティブになる気がします．

なんとなく さんのレス (2010/03/27(Sat) 18:19)

自己レスです．

よく考えてみると光子のプロパゲータはクラインゴルドンで質量項m→0の極限で定義された不変デルタ関数から出発するが，CGでm=0かつ時間成分を落とせばポアッソン方程式であり，その単電荷解の運動量表示であると言える．この逆フーリエ変換はクーロンポテンンシャルであり，そもそも1/rなのですでに理論に内包されている気がする．プロパゲータのゲージ項はＳ行列に利かないが，これはファインマンゲージ以外のダイポ-ルゴーストである縦光子の寄与が物理状態に寄与しない，つまり非物理的状態であることを示しており，残るスカラー光子がクーロン力になるのだろうと思える．とすると，やはり1/r則は経験則であり，deductionされるものではないのだろうか．

nabeyang さんのレス (2010/05/20(Thu) 20:48)

>知りたいのは，有効ポテンシャルの具体的な求め方なのです．

ずっと書きたかったのですが，時間が作れませんでした．いまさらですが ノートを書いたので，お知らせします．

• http://nabeyang.s148.coreserver.jp/uploads/files/20100520_1.pdf

表記法などについて，細かい説明がないので意味不明かもしれないので， そのときは質問してください．