かたより

home > 掲示板 >

このページのPDF版

サイトマップ

かたより

トビラ．．さんの書込 (2010/03/12(Fri) 05:08)

みなさんこんにちは，古典論における電子の双極子能率による電磁波の放射のかたよりについてわからないことがあるので教えてください．まず，多重周期的な電子の双極子能率を

$\mathbf P(t)=\displaystyle\frac{1}{2} \left[ \mathbf C_{ \tau_1\cdots\tau_k } \exp\{ 2\pi i(\tau_1 \nu_1+\cdots+\tau_k\nu_k)t \} +\mathbf C_{-\tau \cdots \tau_k}\exp \{-2\pi i(\tau_1\nu_1+\cdots +\tau_k\nu_k)t \} \right]$

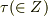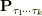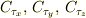とします．（ここで， $\nu$ は振動数で， $\tau(\in Z)$ は整数です）このとき放射される光のかたよりは，この振動するベクトル $\mathbf P_{\tau_1\cdots \tau_k}$ のかたよりに関係します．そして，簡単のため $\mathbf C_{\tau_1\cdots \tau_k}$ の $x,\,y,\,z$ 成分をそれぞれ $C_{\tau_x},\,C_{\tau_y},\,C_{\tau_z}$ と書くことにします．すると本では

の場合には，このベクトルの先端は x-y 平面内で反時計的に円を描くと書いているんですが，どうしてそのようなことが言えるのでしょうか？

多分，オイラーの公式を用いて上述のベクトル 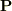$\mathbf P$ を回転行列（？）

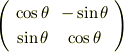
$\left( \begin{array}{cc}\cos \theta&-\sin\theta\\ \sin\theta & \cos\theta \end{array}\right)$

の形で表すんだと思うんですが，どうもうまくそのようにできません．どのように考えればいいのでしょうか？どうかアドバイスお願いします．

Re: かたより

なんとなくさんのレス (2010/03/12(Fri) 10:28)

こんにちは．

Crx=+iCrxは，Cry=+iCrxの間違いではないですか．この式ではCrx=0となると思いますが．

そうであるとすると， Cry=+iCrx,Crz=0の場合は・・・となりますが，これはｚ方向に放射する電磁波，あるいは同じことですが進行方向をｚ軸に取った場合ということだと思います．そうすると，電磁波の性質として振動はｚ軸に垂直なｘｙ平面内で起こることになりますが，その振動を複素平面で表し，ｘ成分をCrx，ｙ成分をCryとしたわけですね．Crx=z1，Cry=z2（z1,z2は複素数)のとき，z2=iz1とすると，z2=exp(iπ/2)z1であり，これはz2がz1を反時計回りにπ/2だけ回転したものであることを示しています．これだけでも合成したもの（の先端が）円を描くことは明らかです．また，偏光ベクトルＺのｘ方向への分解がCrx，ｙ方向への分解がCryですので，今，z1=a+ibとすると，z2=-b+iaとなります．合成Ｚ=z1+z2が実際の偏光ベクトルですが，Ｚ^2=ZZ~=2(a^2+b^2)=z1^2+z2^2(~は複素共役）となって，再び円軌道を描くことが分かります．

Re: かたより

トビラ．．さんのレス (2010/03/12(Fri) 14:27)

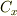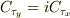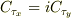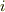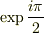なんとなくさんどうもありがとうございます．ご指摘の通り， C_x の成分表示が間違っていたので，修正しておきました．ただし， $C_{\tau_y}=iC_{\tau_x}$ ではなく， $C_{\tau_x}=iC_{\tau_y}$ なんです． = $\exp\displaystyle\frac{i\pi }{2}$ という関係式を用いたのはびっくりしました．円を描くのも理解できました．ありがとうございます．ただ，なぜ反時計回りに回転するのかがやはり理解に苦しみます．確かに，回転行列は 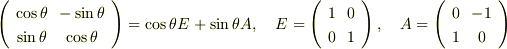$\left( \begin{array}{cc}\cos\theta& -\sin\theta \\ \sin\theta& \cos\theta \end{array}\right)=\cos\theta E+\sin\theta A,\quad E=\left(\begin{array}{cc}1&0\\0&1\end{array}\right),\quad A=\left( \begin{array}{cc}0&-1\\ 1&0\end{array}\right)$ とあらわすことができるので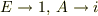，， $\quad E\to 1,\, A\to i$ とおけば，ネイピア数は回転を示している数のように見えますが，でも厳密には 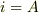i=A とはおけないような気はするので（多分厳密に考えようとするとネイピア数の行列の問題になるかとおもいます），直観的にではなく，本当に反時計回りに回転していることを示すにはどうしたらいいでしょうか？お忙しいところ，返信までしていただいてありがとうございます．（ペコペコ）

Re: かたより

ASA さんのレス (2010/03/12(Fri) 17:33)

ポーラライズドヴェクターPには時間ｔに依存するファクタexp(2πi(ηt))がかかっています(η=?τkνk)．条件は，Crx(t=0)=iCry(t=0)で数学的関係，i=exp(πi/2)よりつまり，時間t=1/4ηたつと時間依存ファクタはiになるから， Crx(t=0)=iCry(t=0)=Cry(t=1/4η) xを横軸，y縦軸とし，ある時刻t=0でx軸と平行なベクターは，t=1/4η後には，y軸と平行なベクターになるので，反時計回りになるわけです．

ちゃんと時間変化を取り入れた説明をしないといけません． (今の話では，進行方向は全く関係ありません．)

Re: かたより

トビラ．．さんのレス (2010/03/13(Sat) 03:32)

ASAさんどうもありがとうございます．ふむふむ，なるほど，大変勉強になります．ただ，時間因子がかかっているとはどういうことでしょうか？掛けられているという意味でしょうか？（初歩的な質問でごめんなさい）つまり，（数学的には）

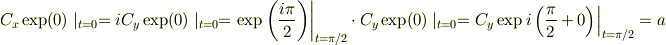
$C_x\exp(0)\mid_{t=0}=iC_y\exp(0)\mid_{t=0}=\left.\exp\left(\frac{i\pi}{2}\right)\right|_{t=\pi/2}\cdot C_y\exp(0)\mid_{t=0}=C_y\left.\exp i\left(\frac{\pi}{2}+0 \right)\right|_{t=\pi/2}=a$

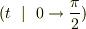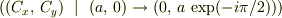と，このように計算すればいいのでしょうか？（ちょっと強引かな？）だとすると， $(t\,\,\mid \,\,0\to \frac{\pi}{2})$ に対して， $((C_x,\,C_y)\,\,\mid\,\,(a,\,0)\to (0,\,a\,\exp({-i\pi/2})))$ となるのでしょうか？この場合，円ではないと思うんですが，どうなんでしょうか？（疑問符ばかりで申し訳ないです．）忙しい中返信してくださってありがとうございます．

Re: かたより

ASA さんのレス (2010/03/13(Sat) 08:48)

C-r...=0で，話を進めます． exp(2πi(ηt))=exp(iωt)とすると，与えられた式は Px=Cxexp(iωt)/2,Py=Cyexp(iωt)/2,Pz=Czexp(iωt)/2:(ωは共通なことに注意) 条件はCx=iCy,Cz=0 ここから直ちにPz=0(常に）第一条件を変形，Cx/Cy=i Px/Py=i=exp(iπ/2) Px=Pyexp(iπ/2)=Cyexp(i(ωt+π/2))/2…(1) 元のaが何を指すか分かりませんが，計算上はこうなるはずです．

実部で話をすると(Cyが実のみという都合のよい位相を選択)， Re(Py)=Cycos(ωt)/2で，上の(1)式から Re(Px)=Cycos(ωt+π/2)/2=-Cysin(ωt)/2 Re(Py)^2+Re(Px)^2=(Cy/2)^2 軌跡は，半径=|Cy|/2の円となってます．

ωtは0→2nπと連続的に変化するので，軌跡は周回軌道になってます．

どっち回りかを調べるためには，No.26555のように軸平行な単位ベクトルが特定時刻間でどのように変化するかを考えると分かりやすいです．

Re: かたより

トビラ．．さんのレス (2010/03/14(Sun) 03:01)

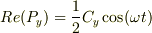
ASAさんどうもありがとうございます．なるほでです．でもこの場合 $Re(P_y)=\frac{1}{2}C_y\cos(\omega t)$

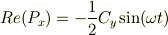
$Re(P_x)=-\frac{1}{2}C_y\sin(\omega t)$

の式に t=0 を代入すると，

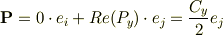
$\mathbf P=0\cdot e_i+Re(P_y)\cdot e_j=\frac{C_y}{2}e_j$

になり，少し時間が進んだ 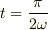$t=\frac{\pi}{2\omega}$ だと

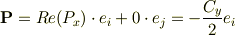
$\mathbf P=Re(P_x)\cdot e_i+0\cdot e_j=-\frac{C_y}{2}e_i$

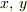（ここで， $x,\,y$ の単位ベクトルをそれぞれ 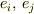$e_i,\,e_j$ とした）となり，ベクトルPは時計回りに回転している気がするのですが，違うのでしょうか？

Re: かたより

ASA さんのレス (2010/03/14(Sun) 06:58)

t=0で Pはej(y軸)に平行，即ち上向き(12時方向)

t=π/2ωで Pはei(x軸)に反平行(-符号に注意)，即ち左向き(9時方向)

明らかに，反時計周りです．

Re: かたより

トビラ．．さんのレス (2010/03/14(Sun) 09:30)

しまった！！たしかに・・・

これで完全に疑問がなくなったと思います．

大変お世話になりました．なんとなくさん，ＡＳＡさんどうもありがとうございました．おかげでスッキリしました．

Re: かたより

なんとなくさんのレス (2010/03/14(Sun) 09:34)

最早，蛇足ですが．

>トビラさん

問題のポーラリゼイションベクトルの最初の項に時間ｔが抜けていますね．

以下はもう不要なら無視してください． ASAさんの書かれたように時間変化のダイナミクスを理解するには時間ファクタを追っかけるのが正当でしょう．軌跡にすれば結局時間パラメタは消えますが．ただ，一つ気になるのは，回転方向を言う場合，暗黙に右手系を仮定している，言い換えればｚ軸の向きを決めているということです．これを進行方向にとっているということだと思います．それと時間ファクタは除いた（ジョーンズベクトルと呼ばれる）成分ベクトルの位相差のみで回転形状と方向は決まってしまいます．今の場合，時間ファクタは（成分に）共通のため，その変化より変化の差（位相差）が問題となります．良く知られたように，これが0,πなら直線，π/2なら円，一般には楕円ですが，今の問題ではすでに書いたように（指摘のように間違っていましたが），Crx=iCryより，Cry=-iCrx=exp(-iπ/2)Crxより，位相差は-π/2，これは左回りとなります．円であることは，これと|Crx|=|iCry|から保証されます．

Re: かたより

ASA さんのレス (2010/03/14(Sun) 15:46)

なんとなくさんちょっと気になるのでコメントしておきます． >回転方向を言う場合，暗黙に右手系を仮定している，言い換えればｚ軸の向きを決めているということです．これを進行方向にとっているということだと思います．これが意味不明です．一般的波動方程式の解を考える時，進行方向と変位方向は関係ありません． (変位方向と進行方向が一致する場合もある) 進行方向と変位方向が直交する特別な波を考えたとしても，その定在波を考える時進行方向云々することは無意味です．今問題にしているのは，あくまで変位方向の時間的変化です．

>暗黙に右手系を仮定している今はz軸関係ありません．敢えて言うならxy軸のアライメントの問題です． x軸が3時方向にy軸が12時方向にという一般的な(中学校で習うような)座標系で考えると左回りになるということです． z軸方向をどっちにとるか(右ねじ，左ねじ)とは，無関係です．

Re: かたより

なんとなくさんのレス (2010/03/14(Sun) 18:47)

>ASAさん

釈迦に説法する気はさらさらありませんので，私見かもしれませんので論争するつもりはありませんが．

>これが意味不明ですポーラリゼーションベクトルは今のような双曲子放射などによる電磁波では前にも書いたジョーンズベクトルで表すことが通念的ですが，この場合，明らかに波数ベクトル，つまり進行ベクトルをｚ軸にとって，右（左）周り（旋光性）を定義しますから，それほど特別なことを言っているわけではないと思いますが．

>進行方向と変位方向が直交する特別な波を考えたとしても，その定在波を考える時進行方向云々することは無意味です．定在波はそもそも進行波でない（進行方向の意味が無い）のでこの言明自体が理解できませんし，特別でもありません．

>x軸が3時方向にy軸が12時方向にという一般的な(中学校で習うような)座標系で考えるとこれこそが暗黙の右手系ということで，ｘ，ｙ軸のアライメント（序列）を決めることそのものだと思いますが．この座標系はｘ⇒ｙ回転の右ねじ方向をｚ軸の正にとるようになっていますから．

Re: かたより

トビラ．．さんのレス (2010/03/14(Sun) 23:13)

なんとなくさん，すみません．ご指摘の通り問題文に時間が抜けてましたので，修正しときます．

おふた方には大変感謝してます．ありがとうございました．

Re: かたより

ASA さんのレス (2010/03/15(Mon) 07:13)

なんとなくさん

>これこそが暗黙の右手系ということで，ｘ，ｙ軸のアライメント（序列）を決めることそのものだと思いますが．この座標系はｘ⇒ｙ回転の右ねじ方向をｚ軸の正にとるようになっていますから．違いますよ．右手系で，z軸正方向から見下ろすのと，左手系で，z軸負方向から見下ろすのとでは，xy軸アライメントは同じになりますから，右手系とか左手系とか持ち出すのが全くのお門違いということです．

Re: かたより

なんとなくさんのレス (2010/03/15(Mon) 09:13)

>ASAさん右手系と左手系で見る向き（正負）を変えるのであれば同じになるのは当たり前で，それなら右回りだ，左回りだというのも見る立場を変えれば同じということですよね．詭弁に思えますが．

Re: かたより

ASA さんのレス (2010/03/15(Mon) 11:13)

なんとなくさん No.26575 勘違いしてますね． >右手系と左手系で見る向き（正負）を変えるのであれば同じになるのは当たり前ででも座標系としては違うので区別できますよね． >それなら右回りだ，左回りだというのも見る立場を変えれば同じということですよね． xyアライメントを固定すれば，座標系にかかわらずに旋回方向は同定できますよね．いいたいことは，3次元の座標系である右手糸と左手系の区別と，ある座標平面に投影された物の旋回の区別とは，異なります．座標系にかかわらず，同じxyアライメントを採ることができるので，旋回方向の区別において右手系やら左手系やらの区別をを持ち出すは，無意味という主張です．ご理解いただけますか．

Re: かたより

なんとなくさんのレス (2010/03/15(Mon) 12:04)

>ASAさん申し訳ないですが，理解できません．ｘｙアライメントを決めるということは，例えば平面上でｘ軸正方向を向き，左手側にｙ軸正方向をとるということだと思います．しかし，これは頭が上であるという了解のもとであって，逆立ちした，頭が下なら逆になります．つまり，ｘｙアライメントを固定するということ自体に”上から見た”等の無意識の仮定があるのではないでしょうか．同じことですが，座標を入れない平面を考えて円を書き，回転方向に矢印を入れます．これは左回りか右回りか区別できる（というか言明できるもの）のでしょうか．この平面を表から見たのと裏から見たのでは逆向きの回転に見える，つまりどちらとも言えなくなります．勿論，裏表を指示することはｚ軸を入れることだし，例えば左手側に円の領域を見るとき左周り，というような決め方（閉曲線で回転方向の定義に使われますよね）は平面のノルマルベクトル（の方向）を与えるのと等価です．それと，何度も書きましたが，ジョーンズベクトルで何故わざわざ進行方向ベクトルを決めたうえでしか回転方向を決められないのか，説明が可能でしょうか．

Re: かたより

ASA さんのレス (2010/03/16(Tue) 07:53)

>ｘｙアライメントを固定するということ自体に”上から見た”等の無意識の仮定があるのではないでしょうか．それは，あなたの勝手な思い込みだと考えます．

>ジョーンズベクトルで何故わざわざ進行方向ベクトルを決めたうえでしか回転方向を決められないのか，説明が可能でしょうか．進行方向は，関係ないです．座標軸アライメントの設定で決まる話です．

次元を増やした場合や次元を少なくした場合で考えると分かりやすいです．

ある電場Eで，∂xE>0でありました(1次元の問題です)．この電場Eは右側に行くほど強くなるとの説明がありました．右手系のみで成立する話なのでしょうか？自分は，座標系にかかわらずx軸アライメントを小学校で習う数直線(定規)と同様にとった場合にいえると説明します．

部分的な座標アライメントの決定のみで，座標系がユニークに決まると思い込んでいる方には，これ以上の説明しても無理なような気がします．

Re: かたより

なんとなくさんのレス (2010/03/16(Tue) 09:00)

成程．問いかけに対する回答も無視されているし，仰っていること自体が私には矛盾していると思えるので，確かにこれ以上の議論は無駄と思います．これで止めます．

[home] [掲示板] [ページの先頭]