曲率の件

曲率の件

悩み人 さんの書込 (2010/03/02(Tue) 15:36)

こんにちは．現在，会社の仕事で構造解析ソフトを作成しようとしており， 曲率の勉強をしていて，このHPにたどり着きました．

このHP，Joh氏執筆の”ベクトル解析”−”曲率と曲率半径”のページによると

d /ds ( r(s) + 1/k e2 ) = e1(s) + 1/k ( - k e1) = 0

この式は，r(s)が点r(s) + 1/k e2' を中心とする半径1/kの円を 表しているとのことです．私にはこの式が円を表していることが わかりません．もう少し詳しく教えていただければ幸いです．

接ベクトルやフレネ＝セレの公式などこの式が現れるまでの説明に 関しては一応理解しているつもりです．

どうぞよろしくお願いいたします．

Re: 曲率の件

Yokkun さんのレス (2010/03/02(Tue) 19:36)

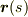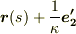> \bm{r}(s) は点 \bm{r}(s)+\frac{1}{\kappa}\bm{e'_{2}} を中心とする半径 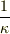\frac{1}{\kappa} の円を表わしている

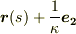\bm{r}(s)+\frac{1}{\kappa}\bm{e_{2}} を中心とする

の間違いだと思われます．

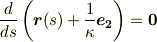
\frac{d}{ds} \left( \bm{r}(s)+\frac{1}{\kappa}\bm{e_{2}} \right) =\bm{0}

により，

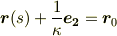
\bm{r}(s)+\frac{1}{\kappa}\bm{e_{2}} = \bm{r}_0

と置きます．ここに 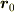\bm{r}_0 は定ベクトルとなり，定点を指示しています．すると，

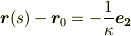
\bm{r}(s) - \bm{r}_0 = -\frac{1}{\kappa}\bm{e_{2}}

と書けますが，左辺は定点を始点，曲線上のある点を終点とするベクトルを意味します．そして，右辺は今考えている曲線上のある点における主法線方向と逆を向く長さ 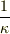\frac{1}{\kappa} のベクトル（結果的に円の中心から円周に向かう半径ベクトル）を指します．すなわち，上の式は

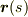「 \bm{r}(s) で指示される曲線上の点から見ると，主法線方向に 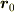\bm{r}_0 で指示される定点があり，その距離が 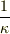\frac{1}{\kappa} である．」

ということを表現しています．これは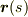， \bm{r}(s) で記述される平面曲線が，定点 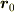\bm{r}_0 を中心とし，半径が 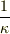\frac{1}{\kappa} の円であることを示していると思います．最後の式の2乗（自身との内積）をとって，たとえば直交座標で表現すれば，ただちによく知られた円の直交座標による表式を得ますね？

Re: 曲率の件

悩み人 さんのレス (2010/03/03(Wed) 11:11)

Yokkun様

大変よく理解でき，心が晴れ晴れいたしました． 明快なご回答ありがとうございました．