インダクタンスLとMの関係
インダクタンスLとMの関係
kk さんの書込 (2010/02/26(Fri) 05:36)
大学2年で電気回路を勉強しています.
相互インダクタンスMの2つのインダクタンスに同じ方向に電流が流れているとき
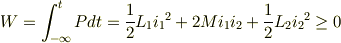
したがって
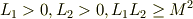
とノートに書いてあったのですが 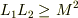 の導出がわかりません.
の導出がわかりません.
相加平均>=相乗平均 など利用してみたのですが導き出せず
また検索しても 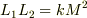 という式が出てくるばかりでした.
という式が出てくるばかりでした.
どなたかご教授お願いします.
大学2年で電気回路を勉強しています.
相互インダクタンスMの2つのインダクタンスに同じ方向に電流が流れているとき
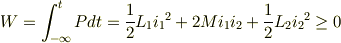
したがって
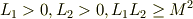
とノートに書いてあったのですが 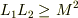 の導出がわかりません.
の導出がわかりません.
相加平均>=相乗平均 など利用してみたのですが導き出せず
また検索しても 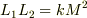 という式が出てくるばかりでした.
という式が出てくるばかりでした.
どなたかご教授お願いします.