電気回路
電気回路
DOG さんの書込 (2010/02/21(Sun) 14:57)
電磁気分野からの質問です.
問題の電気回路は以下のURLの通りです.
この質問では交流は関係ありません.
次の2つの問いについて質問があります.
1.スイッチをa側にとじて十分に長い時間が経過したのち,抵抗1で消費される電力を求めよ
2.その後スイッチを開いた.スイッチを開いた直後から十分に長い時間が経過するまでに,回路で消費されるエネルギーを求めよ.
まず1についてです. この問いでは「スイッチをa側にとじて十分に長い時間が経過したのち」と書いてあり,そのときは抵抗1にしか電流が Vo/R1 の大きさで流れないことが分かるから, 求める電力は Vo^2/R1 というのは分かります.
もしこれが, 「スイッチをa側に閉じた直後から十分時間が経過するまでにR1で消費される電力を求めよ」 ということになったら,その電力を求めることは可能なのでしょうか?・・・
次に2についてです. この問いの答えを一応自分で出して,合っていました.(下のURLに答えを貼っています)
この問題を解いたのは2,3ヶ月ぐらい前のことでして,なぜこう考えたかを覚えていなくて,今自分なりに考えたのが,
?スイッチを開く直前にはコイルに電流 Vo/R1 が流れており,かつ,コンデンサーには電位差 Voで充電が完了している.
?それが十分に時間が経過すると,電流が0になり,もともとたまっていた全エネルギーが消費される.
この考え方で合っていますでしょうか?
どなたかご教授お願いします.
Re: 電気回路
Yokkun さんのレス (2010/02/21(Sun) 17:44)
>その電力を求めることは可能なのでしょうか?・・・
可能だと思われますが,大学レベルになるでしょう.次の微分方程式を解くことになるのではないかと思います.
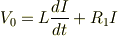
ぎりぎり高校レベルでも解けるのかもしれませんが,大学入試レベルでそれを求められることは,まずないと思われます.以下,参考まで.
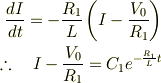
 のとき,
のとき, 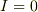 より
より 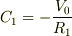 .したがって,
.したがって,
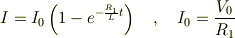
すると,数学的に要求される積分範囲は  ということになるので,・・・あれれ,やはり解答は不可能でしたね.本質的に解けない問題でした.^^;
ということになるので,・・・あれれ,やはり解答は不可能でしたね.本質的に解けない問題でした.^^;
2は合っていると思います.
Re: 電気回路
DOG さんのレス (2010/02/21(Sun) 20:05)
Yokkunさん,返答ありがとうございます.
やはり解答不可能でしたか・・・
なんとなく,ふと自分で思ったことなのであまり気にしてはいなかったのですが,Yokkunさんに手間をとらせてしまって申し訳ありませんでした.
2は合っているようで安心しました.
もし,2の状態の回路で抵抗R1,R2がなく,有名なLC回路であったら電流は永遠と流れると考えてもよいのでしょうか?
抵抗があるからジュール熱が発生して,いずれは電流が0になると考えてもよろしいのでしょうか?
Re: 電気回路
Yokkun さんのレス (2010/02/21(Sun) 20:54)
>永遠と流れると考えてもよいのでしょうか?
はい,その通りです.もちろん,あらゆる点で理想化を裏切る現実が横たわっているのですね.
>抵抗があるからジュール熱が発生して,いずれは電流が0になると考えてもよろしいのでしょうか?
そういうことになります.