円柱型導線のインダクタンス
円柱型導線のインダクタンス
march さんの書込 (2010/02/21(Sun) 04:37)
はじめまして. 大学2年で電磁気の問題で理解に苦しむ箇所があります.
2つあるのですがどちらも円柱型導線のインダクタンスに関連した問題です.
(1)
半径  ,長さ
,長さ 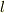 の円柱型導線の外部インダクタンス
の円柱型導線の外部インダクタンス 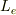 を求める問題で
を求める問題で
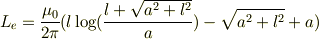
と求めることができます.
※参考 [1] http://reg.is.t.kanazawa-u.ac.jp/~nagayama/TA/denji2/index.php?plugin=attach&pcmd=open&file=070628.pdf&refer=%B1%E9%BD%AC%CC%E4%C2%EA%B2%F2%C5%FA [2] http://flex.ee.uec.ac.jp/~t-kimura/denjiki2/self-inductance.pdf
一方で,長さ 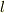 の導線(太さ無視)を2本平行に間隔
の導線(太さ無視)を2本平行に間隔  で並べ
同じ向きに電流が流れる際のインダクタンスMは
Neumannの式と呼ばれる公式により
で並べ
同じ向きに電流が流れる際のインダクタンスMは
Neumannの式と呼ばれる公式により
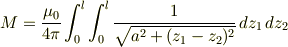
で求まるそうですが
この  が先の外部インダクタンス
が先の外部インダクタンス 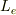 と全く同じになります.
と全く同じになります.
両者は値として単に同じではなく 同じ概念を別々の方法で計算しているように思えてしまうのですが どうして両者が同じになるのでしょうか?
(2)
先ほどの半径  の円柱型導線の内部インダクタンスを求める際に
参考[2]において,磁束
の円柱型導線の内部インダクタンスを求める際に
参考[2]において,磁束 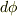 から鎖交磁束
から鎖交磁束 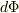 を求める際に
を求める際に
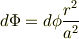
とするのはどうしてなのでしょうか?
文中では磁束 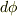 と鎖交するのは
半径
と鎖交するのは
半径  内の電流だからと説明されていますがそこがわかりません.
内の電流だからと説明されていますがそこがわかりません.
磁束が「鎖交する」こととは
ループ状の回路だったら回路の中を磁束が抜けることだったり
また,N回巻いてあるコイルだったら鎖交磁束は 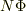 になる
と言うのはわかりますが,
上記の場合はそれらの「鎖交」のイメージとだいぶ離れていて理解できません.
になる
と言うのはわかりますが,
上記の場合はそれらの「鎖交」のイメージとだいぶ離れていて理解できません.
長いこと躓いていて困っています. よろしくお願いします.