単振動

重心から見たPの振幅を求めたのですから，ゴールまではあとちょっとだったのですね．考察は正しく，手順も間違いなかったのですから自信をもってください．ただし，入試対策となれば解法の効率がものをいいます．また，簡明でエレガントな解法ほど，より基本的でありながら（基本的だからこそ）深い洞察を必要とするものなのです．でも，それを理解するとAha!がまた増えて，柔軟な見方ができるようになっていきます．たとえば，今回のような相対運動の問題は，同じ運動方程式を数通りの立て方と見方ができます．

静止系から見た立場

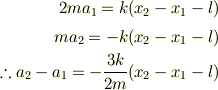
$2ma_1 = k(x_2-x_1-l)\\ma_2 = -k(x_2-x_1-l)\\\therefore a_2-a_1 = -\frac{3k}{2m}(x_2-x_1-l)$

エネルギー保存

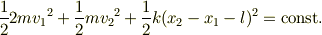
$\frac{1}{2}2m{v_1}^2 + \frac{1}{2}m{v_2}^2 + \frac{1}{2}k(x_2-x_1-l)^2={\rm const.}$

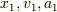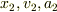x_1,v_1,a_1 はQ'， x_2,v_2,a_2 はPの座標と速度，加速度です．

重心とともに動いてばねを分割して考える立場

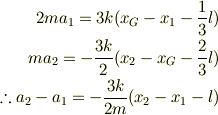
$2ma_1 = 3k(x_G-x_1-\frac{1}{3}l)\\ma_2 = -\frac{3k}{2}(x_2-x_G-\frac{2}{3}l)\\\therefore a_2-a_1 = -\frac{3k}{2m}(x_2-x_1-l)$

エネルギー保存

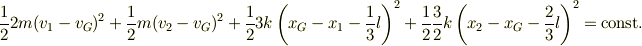
$\frac{1}{2}2m(v_1-v_G)^2+\frac{1}{2}m(v_2-v_G)^2+\frac{1}{2}3k\left(x_G-x_1-\frac{1}{3}l\right)^2+\frac{1}{2}\frac{3}{2}k\left(x_2-x_G-\frac{2}{3}l\right)^2={\rm const.}$

※ただし，Q'，Pそれぞれ単独でも成立する．周期を求めるだけならともかく，ばねを分割する方法は，エネルギー保存では冗長なことがわかります．結局1本にまとめたのと結果は同じだからです．

これをQ'，Pに分けたものが，DOGさんが解答された見方ですね？重心は等速度運動するので，慣性力を考える必要がありません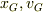． x_G,v_G は重心の座標と速度です．

相対変位の単振動と見る見方

どの立場から見ても，単振動を見極めるための計算の結果は，結局この相対変位についての運動方程式に落ち着きます．なお，この運動方程式を直接立てるのは「相対変位」と「換算質量」について知っていないと無理ですが，これはQ'とともに動く立場で慣性力を考慮しても得られます．DOGさんはこの方法をとられたのかな？

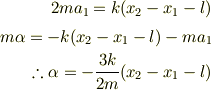
$2ma_1 = k(x_2-x_1-l)\\m\alpha = -k(x_2-x_1-l) - ma_1\\\therefore \alpha = -\frac{3k}{2m}(x_2-x_1-l)$

DOGさんが正しくたてた運動方程式です．これは，質量2m/3の質点があたかも相対変位を変位として振動するかのように書かれています．この質量は「換算質量」と呼ばれるものです．

さてエネルギー保存はというと，

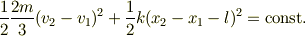
$\frac{1}{2}\frac{2m}{3}(v_2-v_1)^2 + \frac{1}{2}k(x_2-x_1-l)^2 = {\rm const.}$

と書けるのです．これが上のひとつにまとめられた運動方程式から自然に導かれる「単振動」のエネルギー保存です．エネルギー保存では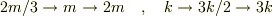， $2m/3 \rightarrow m \rightarrow 2m\quad,\quad k \rightarrow 3k/2 \rightarrow 3k$ の同時置き換えが可能で，そうするとDOGさんの考えた重心から見てばねを分割した場合のP，Q’単独のエネルギー保存になります．

なお，以上において 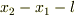v_2-v_1 <--- x_2-x_1-l の時間微分 a_2-a_1 <--- v_2-v_1 の時間微分になっていることに注意すると，すっきりと飲み込めてくるものがあるかもしれません．

※ちょっと調子にのって遊びすぎました．読み流してください．

Re: 単振動

DOG さんのレス (2010/02/18(Thu) 21:06)

す・・・・すごいです・・・・

ここまで話題が広げられるなんて感激です．

本当にいい勉強になります．

ありがとうございました．

[home] [掲示板] [ページの先頭]