電気回路・単振動
電気回路・単振動
DOG さんの書込 (2010/02/16(Tue) 20:53)
二つ質問があります.
まずこちらは電気回路です.
全ての内部抵抗は無視できます.
物理量は全て画像に書いてあるとおりです.(手抜きですみません・・・・) 抵抗の単位はオームです.
ここで次のような問いがあります.
R2(可変抵抗)を0から次第に増やしていくと,電流計に電流が流れ始めた. このときのR2の抵抗値を求めよ.
という問いで,電流計に電流が流れ始めるときはダイオードの両端の電位は等しいから,求める抵抗値をRとすると,
12R/(R+4) = 6 よってR=4
と教えられましたが,この等式が成り立つ意味が分かりません.
R2に 12R/(R+4) の電圧がかかることは分かりますが,なぜそこの電位差が6ボルトなのでしょうか.
R3とE2間の電位差が12R/(R+4)ボルトであって,なぜR3での電圧降下を考えていないのでしょうか?
二つ目は単振動についてです. 下のURLに図を載せます.
小球R P Qは質量が全てm バネ定数:k バネの自然長:L です.
今Rが速度v0でQに近づき,衝突直後QとRは一体(これをQ'とする)となり,速度Vで運動を始める.
問題の流れとしては,Q'からみたPの相対加速度を出し,この式から,Q'からみたPの運動が単振動であると分かり,その周期と振幅を求めよというところです.
ちなみにそのQ'からみたPの相対加速度の運動方程式は
α=-3k(x-L)/2m で,周期はだせました.
ここで振幅Aをだそうとして,自分は力学的エネルギー保存則をつかって,
mV^2/2 = kA^2/2 から A=・・・ と出したのですが,
答えが, V=ωA より A=V/ω でだしていて,自分の答えとは違っていました. なぜ自分の式だとダメなのでしょうか?
どなたか教えて下さい.
Re: 電気回路・単振動
Yokkun さんのレス (2010/02/16(Tue) 22:27)
よくばりましたね.混乱しますので,コピペして後半を分割されることをお薦めします.
ダイオードに電流が流れ始めるまで,R3には電流が流れていませんね? ですから,流れ始めの限界においてR3の電圧降下はゼロです.
Re: 電気回路・単振動
DOG さんのレス (2010/02/16(Tue) 23:43)
Yokkunさん,いつも返答感謝しています.
ごめんなさい,文章長くて見づらかったですね・・・・
もうすぐ入試も控えていて,気持ちばかり焦ってしまいました.
後半は新スレとして書き込みたいと思います.
>ダイオードに電流が流れるまで,R3には電流が流れていません
え,そうなのですか?? しかしコンデンサー側からまわった電流はR3を通過しませんか?
Re: 電気回路・単振動
Yokkun さんのレス (2010/02/17(Wed) 10:04)
回路を構成してからある程度時間がたっていると考えて,コンデンサーは6Vに充電が完了しているとしてよいと思います.その状態でダイオードの電圧はまだ順方向になっていないので,R3への電流はストップしていると考えるべきでしょう.
Re: 電気回路・単振動
DOG さんのレス (2010/02/17(Wed) 20:16)
なるほど・・・・
問題文中に「十分時間が経過した」と書いていなくても,それを読み取らないといけないということなのでしょうか?
もし本番で,今のような設問がでてきたら, 「これは本当に充電完了したと見てもよいのか?・・・・」
というふうに深く考えてしまってパニックになりそうで怖いです...
Re: 電気回路・単振動
Yokkun さんのレス (2010/02/17(Wed) 21:05)
入試問題などでは,後でつっこまれるのを避けるためもあってか,大体かいてあるのですが,現実には特別な大容量コンデンサや大きな抵抗を用いなければ,あっという間です.
これはちょっと難しいかもしれませんが,電気抵抗Rと電気容量Cを直列に定電圧Vにつないで充電する場合,コンデンサーの電気量について
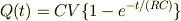
が成り立ちます.すると,t>>RC で充電完了とみることができます.今回の問題では抵抗は数Ω,コンデンサは数μFですから,おおざっぱな見積もりでRCは10^(-5)秒程度でしょうか.
また,何よりも,充電完了していなければR3の電圧降下は不定ですから,問題として成立しないという点を考えれば,不安は解消できるでしょう.そこを読み取ることが大切だと思います.題意を読み取る,まさに出題者の意図をくむ・・・ということでしょうか?
Re: 電気回路・単振動
DOG さんのレス (2010/02/17(Wed) 23:28)
大学の物理学では,コンデンサーを充電する途中経過までも学ぶのですね( ゜o゜ )
自分は物理に苦戦してはいますが物理自体は好きなので,ものすごい興味をそそられます.
>充電完了していなければR3の電圧降下は不定 たしかにそうですよね・・・・ 最初自分で文字を置きながらやっていましたが,どうやっても無理でしたもの・・・
Yokkunさん,ありがとうございました.
Re: 電気回路・単振動
Yokkun さんのレス (2010/02/18(Thu) 01:48)
蛇足ですが.
「途中経過」までは,高卒レベルからタッチの差です.参考までに・・・
抵抗の電圧降下とコンデンサーの電圧の和は,電源電圧に等しいので
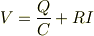
ここで,
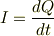
の関係から
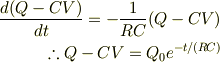
t=0 でQ=0 より
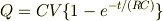
を得ます.