円筒の慣性モーメント
円筒の慣性モーメント
tt さんの書込 (2010/02/16(Tue) 20:35)
次の問題について質問があります. (問)質量M,半径a,長さがhの円筒の中心を通り,円筒に垂直な回転軸の周りの慣性モーメント を計算せよ.
これは円筒の厚さは考えなくていいものだと考えるべきでしょうか? そうだとしたら,慣性モーメントI=M(a^2)
仮に,外半径a,内半径bだとすれば, 厚さdrの円筒を考え密度ρ=M/(πh(a^2-b^2)) 微小部分の体積2πrhdr I=∫[b→a](r^2)ρ2πrhdr =∫[b→a](r^2)M2πrh/{πh(a^2-b^2)}dr =M(a^2+b^2)/2 となったのですが,これであってますか? お願いします.
Re: 円筒の慣性モーメント
Yokkun さんのレス (2010/02/16(Tue) 22:19)
問題を読む限り,中味のつまった円柱でよいと思われます. でも,よく問題を読んでください.
「円筒の中心を通り,円筒に垂直な回転軸の周りの慣性モーメント」
円柱側面を串刺しにした軸まわりの慣性モーメントと読めます.その場合,円筒を輪切りにして,円板の直径を軸とする慣性モーメントをまず求めて,平行軸の定理を用いて回転軸まわりの値に直してから,積分するのが普通の方法です.
また,後半で計算されたものは題意に合ってはいませんが,ちなみに
I = I(a) - I(b) = 1/2・M(a)a^2 - 1/2・M(b)b^2
※(a),(b)は半径a,bの円筒の値を示す.
と考えるのが簡便です.慣性モーメントは質量と同じで,軸が同じならば加法性が成立します.ついでに符号がまちがってますね?^^;
※マルチポストは禁止されています.先のポストをただちに閉じられることをお薦めします.
Re: 円筒の慣性モーメント
tt さんのレス (2010/02/17(Wed) 00:05)
回答ありがとうございます. 円柱側面を串刺しにした軸回りの慣性モーメントはまた, 考えてみます. 後半の計算ですが,符号が-になりません. やった計算を書いてみます. I=∫[b→a](r^2)ρ2πrhdr =∫[b→a](r^2)M2πrh/{πh(a^2-b^2)}dr =∫[b→a](r^3)2M/(a^2-b^2)dr =(a^4-b^4)M/{2(a^2-b^2)} =(a^2+b^2)(a^2-b^2)M/{2(a^2-b^2)} =M(a^2+b^2)/2 となってしまいます.どこで間違えてしまったのかわかりません. お願いします.
Re: 円筒の慣性モーメント
Yokkun さんのレス (2010/02/17(Wed) 10:19)
ごめんなさい.ttさんので合ってました.
Ia = 1/2・ρπa^2h×a^2 Ib = 1/2・ρπb^2h×b^2 I = Ia - Ib
ということですね.
Re: 円筒の慣性モーメント
tt さんのレス (2010/02/17(Wed) 20:53)
>Ia = 1/2・ρπa^2h×a^2 >Ib = 1/2・ρπb^2h×b^2 >I = Ia - Ib
これだと I=1/2・M(a^2-b^2) となってしまうんですが,なぜでしょうか? 答えはI=1/2・M(a^2+b^2)だと思うのですが.
Re: 円筒の慣性モーメント
Yokkun さんのレス (2010/02/17(Wed) 21:15)
あ,私と同じワナにかかりましたね?^^;
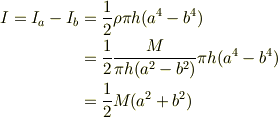
です.積分を振り返ってみると,全く同じ計算ですよね? このρとMにかかわる混乱は,よくはまるのでお互い気をつけましょう.