ばねの問題
ばねの問題
石 さんの書込 (2010/02/10(Wed) 00:24)
今晩は. 私は資源系の大学に通う学生です. 高校時代に物理を履修していなかった為, 大学の物理には苦しめられています….
次の問題について質問です. (この問題は,地震学の授業で出題されました)
質量  の物体を,ばね定数がそれぞれ
の物体を,ばね定数がそれぞれ 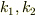 のばねで,
ばねが平行になるように天井につるした.
のばねで,
ばねが平行になるように天井につるした.
 軸は釣り合いの位置を0とし,鉛直下向きに正の方向をとるものとする.
この時,以下の問いに答えよ.
軸は釣り合いの位置を0とし,鉛直下向きに正の方向をとるものとする.
この時,以下の問いに答えよ.
(1)
この系について,外力  と変位
と変位  に関する運動方程式をつくれ.
に関する運動方程式をつくれ.
(2)
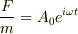
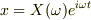 とした時,(1)の方程式を解き,
とした時,(1)の方程式を解き, 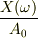 を求めよ.
を求めよ.
(3) この系はばね振り子であるが,そのままでは地震計として用いることができない. その理由を,(2)の解を用いて説明せよ.
※教科書は『初等力学』(甲木伸一.1995,裳華房)を使用しています.
※(1)は,以下のように考えました.
ニュートンの運動方程式より,
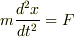 …?
…?
フックの法則より
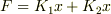 …?
…?
よって,?式・?式より,
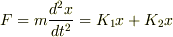 …?
となる.
…?
となる.
自分はこのように解きましたが,この後がわかりません. よろしくお願い致します.
Re: ばねの問題
Yokkun さんのレス (2010/02/10(Wed) 10:23)
外力というのは,ばね振子という系の「外」からの力を指していると思います.与えられた問題では,地震によって生じる力(慣性力)に相当するわけでしょう.つりあいの位置からの変位をとっているので,重力は自然長からつりあいの位置までのばねの伸びによってキャンセルされますから考慮しなくてよいのですが,内力(ばねによる復元力)と外力は区別しなければなりません.
また,運動方程式は本来ベクトル方程式なので,設定された座標軸にしたがって符号により方向を示す必要があります.外力は指定された座標軸にのっとって下向きに  としてよいと思いますが,復元力はどちらむきかよく考えてください.
としてよいと思いますが,復元力はどちらむきかよく考えてください.
Re: ばねの問題
Yokkun さんのレス (2010/02/10(Wed) 14:39)
そうですね.ただし,  の文字は外力として使われている関係から,石さんの使われた
の文字は外力として使われている関係から,石さんの使われた  は,復元力を取り出しただけの異なる意味であり,運動方程式の右辺は外力も含めた合力とすべきですから,
は,復元力を取り出しただけの異なる意味であり,運動方程式の右辺は外力も含めた合力とすべきですから,
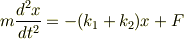
となると思います.
Re: ばねの問題
石 さんのレス (2010/02/10(Wed) 19:43)
ありがとうございます.
従って,(1)の答えは
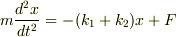 …?
…?
となるんですね?
そうすると,(2)は,?の微分方程式を解くことになりそうですが,
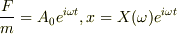 より,?式は,
より,?式は,
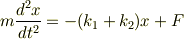
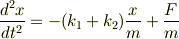
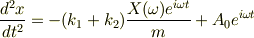
取り敢えず,ここまではわかります. しかし,微分方程式の解き方は習っておらず,苦戦しています….
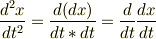
ここで,
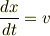
より,
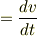
となる,
そして,両辺を微分すれば, 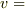 の式になり…
と言う事は習いましたが,今回求めたいのは
の式になり…
と言う事は習いましたが,今回求めたいのは  ではないので,
この知識は使えないですかね….
ではないので,
この知識は使えないですかね….
Re: ばねの問題
Yokkun さんのレス (2010/02/10(Wed) 19:48)
>微分方程式の解き方は習っておらず,苦戦しています….
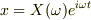
と解の形を仮定しているのですから,直接に「解く」必要はありません.
代入して,微分を実行するだけですよ.  は時間的には定数と仮定されていると思いますので,
は時間的には定数と仮定されていると思いますので,
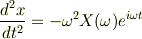
です.
Re: ばねの問題
Yokkun さんのレス (2010/02/11(Thu) 14:09)
もう微分は終わっています.
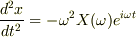
石さんは,積分しようとして微分をしちゃいました. もう微分も積分も必要ないんです.私が代わりに微分しておきました.
あとは,この結果を運動方程式に代入します.すると両辺のすべての項に 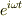 がつきますから,とってしまうことができますね?そこから
がつきますから,とってしまうことができますね?そこから 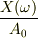 を導けばよいのだろうと思います.
を導けばよいのだろうと思います.
Re: ばねの問題
石 さんのレス (2010/02/11(Thu) 18:31)
失礼しました.
即ち,
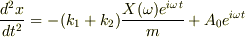 …?
…?
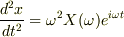 …?
…?
?式を?式へ代入すると,
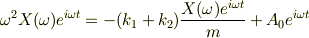
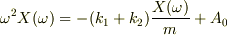 …?
…?
ということでしたね. すみませんでした. 問題で「解け」と指示されていたので,解く能力もないのに 解くことばかり考えていました….
ここで,求めるものは, 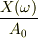 だから,
?式の両辺を
だから,
?式の両辺を 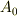 で割ると,
で割ると,
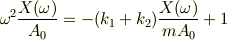
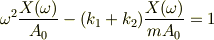
![[{\omega}^{2} - \frac{(k_1 + k_2)}{m}]\frac{X(\omega)}{A_0} = 1](http://hooktail.maxwell.jp/bbslog/a43e0cf0fd76ed24e8e2e34fd4deb5ac.png)
 …?
…?
と,なりました. これが,(2)の答えは,これでいいですか?
Re: ばねの問題
Yokkun さんのレス (2010/02/11(Thu) 18:55)
初め,左辺のマイナスがぬけ,続いて計算途中の移項でまた符号違い.都合2か所で符号がひっくりかえりました.
通常
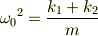
と置いてすっきりさせます. 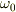 は系の固有角振動数と呼ばれ,外力なしで(重力のみで)自然に振動させるときの角振動数です.
は系の固有角振動数と呼ばれ,外力なしで(重力のみで)自然に振動させるときの角振動数です.
Re: ばねの問題
Yokkun さんのレス (2010/02/11(Thu) 19:22)
符号をチェックしてください(2箇所ひっくり返ってます).
Re: ばねの問題
Yokkun さんのレス (2010/02/11(Thu) 21:27)
よいと思います.そうしますと,(3)はどうでしょうか?
地震による慣性力(加速度)の振幅 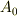 に対して,系の振幅
に対して,系の振幅 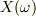 は,ゆれの速さ
は,ゆれの速さ  に依存して大きく変わることになりますね?特に
に依存して大きく変わることになりますね?特に 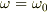 は共振状態を示します.
は共振状態を示します.
Re: ばねの問題
Yokkun さんのレス (2010/02/12(Fri) 12:57)
は重要な結果です.現実にこれが無限大にならないのは,立てた運動方程式に不備があるからですね?つまり,空気抵抗やばねそのものが性質としてもつ減衰や,弾性限界の考慮がされていないのです.現実には無限大にはなりえないのですが,ときには弾性限界を超えてしまうほどに振幅が大きくなるというのが共振現象の特徴です.このように特定の振動数で振幅がとてつもなく大きくなったり,あるいは逆に
と
のギャップが激しいときには,地面が大きく揺れてもこの「地震計」はピクリともしない,ということになります.これでは地震計に使えませんね?この振幅が振動数に大きく依存していることこそ,この系が地震計に向かない点なのでしょう.
Re: ばねの問題
ミュフ猫 さんのレス (2010/02/12(Fri) 20:47)
横レス,失礼します.
なるほど.数学的には,
ω = ω0
のときは,そもそも,
x = X(ω)・exp{iωt}
という仮定そのものが誤りですか. 全体のエネルギーで考えてたら,大ハマリしてしまいました・・・.
スレ汚し,すみません.m(_ _)m
Re: ばねの問題
Yokkun さんのレス (2010/02/13(Sat) 22:46)
いえ,抵抗や弾性限界で共振時の振幅の上限はついても,それはまさにゆれを再現していないことになりますし,逆に地震によるゆれの振動数が固有振動数とかけ離れているとちっとも振れないことになります.ですから,そのままでは使い物にはならないということですね.実際の地震計がどうなっているかはわかりませんが,現実の地震の揺れを振動数や振幅において想定し,その範囲で地面のゆれをある程度正確に再現するようなものでなければならないと思います.
Re: ばねの問題
石 さんのレス (2010/02/14(Sun) 00:43)
そうですか. 確か,実際の地震計は「倒立振り子」なるものを使っているものもや,ばね振り子に「制動器」(流体摩擦による制動を働かせる装置)というものを使って共振を弱めているものもある,と言う話を聞いたことがあります. 地震計も種類によって,構造も様々だそうです. 自分は完全には理解できていないので,現在こうしてじみちに少しずつですが,勉強しているところです….
Re: ばねの問題
Yokkun さんのレス (2010/02/14(Sun) 08:01)
がんばってください.
Re: ばねの問題
石 さんのレス (2010/02/14(Sun) 12:47)
Yokkunさん,短い間ではありましたが大変お世話になりました. どうもありがとうございました. またどこかでお目にかかりましょう.
それでは,失礼します.
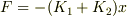
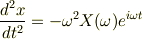
 2回微分すると
2回微分すると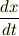
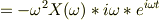
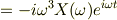
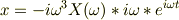
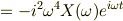
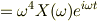
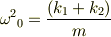
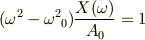
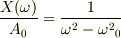 …?
…?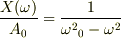 …?
…?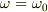
 となり,成り立たないのではないですか?
となり,成り立たないのではないですか?