置換なのですが・・・

置換なのですが・・・

れいか さんの書込 (2010/02/03(Wed) 18:38)

置換が

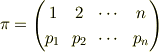
\pi = \begin{pmatrix}1 & 2 & \cdots & n\\ p_1 & p_2 & \cdots & p_n\end{pmatrix}

のときに，この置換をｎ変数関数に作用すると

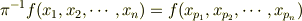
\pi^{-1}f(x_1,x_2,\cdots ,x_n)=f(x_{p_1},x_{p_2},\cdots ,x_{p_n})

が成り立つようなのですが，どうしてπが逆元なのかわかりません．

私はπをそのまま 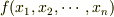f(x_1,x_2,\cdots ,x_n) に作用すると 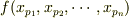f(x_{p_1},x_{p_2},\cdots ,x_{p_n}) になるように思うのですが．

どなたかよろしくお願いします．

Re: 置換なのですが・・・

anon さんのレス (2010/02/04(Thu) 18:28)

n次の置換がn変数関数に作用する，ということの定義はどんなものでしたか？ （つまり，πを置換，fを関数としたとき，π(f)はどんな関数になりますか？）

Re: 置換なのですが・・・

れいか さんのレス (2010/02/04(Thu) 19:02)

πをｆに作用させると

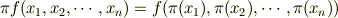
\pi f(x_1,x_2,\cdots ,x_n)=f(\pi(x_1),\pi(x_2),\cdots ,\pi(x_n))

となると思います．

そして，

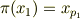
\pi(x_1)=x_{p_1}

だと思うので，やっぱりπを作用させるのではないのかと思います．

あの，やっぱりなぜ逆元なのかわかりません・・・

お願いします．

Re: 置換なのですが・・・

anon さんのレス (2010/02/08(Mon) 10:22)

「こうだと思う」という表現がちょっと引っかかります．

教科書か何かで「定義」を確認して，まさにそこに記述されていたことを， （奥ゆかしさゆえに）「思う」と表現しているのでしょうか？ それとも，教科書の定義を確認したが，なぜそう定義されているのか納得いかずに， 「（教科書の定義とはちがって）こういうふうに定義するほうが自然だと思う」 という意見を持っているということでしょうか？

先に進む前に，ちょっとその点だけ確認させていただけますか？