慣性能率
慣性能率
asdf さんの書込 (2010/02/02(Tue) 22:30)
大学1回です.
半径a,質量M,密度一様な球が,表面の点Oを通る水平軸のまわりに自由に回転できる.それが静止している状態で,質量m,速さvの弾丸が水平方向から軸に垂直に打ち込まれ,弾は極めて短時間で球の中心で止まり,球は水平軸の周りに微小振動を始めた.
という問題で,軸のまわりの慣性能率Iは,
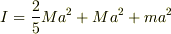
となっているのですが,この 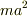 を足す理由は何でしょうか?
を足す理由は何でしょうか?
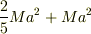 は,平行軸の定理
は,平行軸の定理 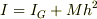 を使ったというのはわかるのですが,なぜ,mにa^2をかけたものを足しているのでしょうか.
を使ったというのはわかるのですが,なぜ,mにa^2をかけたものを足しているのでしょうか.
Re: 慣性能率
yama さんのレス (2010/02/02(Tue) 22:56)
球に弾丸が加わったので,水平軸のまわりの弾丸の慣性能率を加えたものが全体の慣性能率になります.
Re: 慣性能率
asdf さんのレス (2010/02/02(Tue) 23:34)
回答ありがとうございます.
平行軸の定理で,I_Gは,重心を通る軸のまわりの慣性能率なので,今回の場合は, 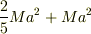 が,I_Gになるということでしょうか.だったら確かに,弾は球の中心(水平軸から距離a)にあるので,あのような式になりますが,水平軸は重心を通っているわけではないのでこの定理を適用できないと思ったのですが,どうなのでしょうか?
それとも,質点の慣性能率がma^2になり,それを足しているのでしょうか?
また,2つ以上の物体があるとき,単純にそれらの慣性能率の和をとれば,その系の慣性能率が求まるのでしょうか?
が,I_Gになるということでしょうか.だったら確かに,弾は球の中心(水平軸から距離a)にあるので,あのような式になりますが,水平軸は重心を通っているわけではないのでこの定理を適用できないと思ったのですが,どうなのでしょうか?
それとも,質点の慣性能率がma^2になり,それを足しているのでしょうか?
また,2つ以上の物体があるとき,単純にそれらの慣性能率の和をとれば,その系の慣性能率が求まるのでしょうか?
Re: 慣性能率
yama さんのレス (2010/02/02(Tue) 23:47)
弾丸の大きさを無視して質点と見なしたわけです.
その場合,重心のまわりの慣性能率が(質点の慣性能率が0なので)弾丸の有無に無関係に 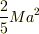 となるので,平行軸の定理を適用しても結果は同じになります.
つまり重心のまわりの慣性能率
となるので,平行軸の定理を適用しても結果は同じになります.
つまり重心のまわりの慣性能率 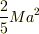 に,軸のずれによる変化
に,軸のずれによる変化 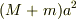 を加えるわけです.
を加えるわけです.
>また,2つ以上の物体があるとき,単純にそれらの慣性能率の和をとれば,その系の慣性能率が求まるのでしょうか?
そうです.
Re: 慣性能率
asdf さんのレス (2010/02/03(Wed) 01:54)
ありがとうございました.
Re: 慣性能率
asdf さんのレス (2010/02/03(Wed) 18:34)
すいません.もう一度同じ問題で質問させてください.
この本来の問題は,振動の周期とふれ角の最大値を求めよ(ふれ角は十分小さい)
というものなのですが,周期は分かったのですが,ふれ角について疑問に思ったことがあります.
運動方程式 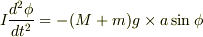 より,
より,
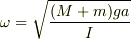 (途中式は省略しました)
となり,ふれ角の最大値を
(途中式は省略しました)
となり,ふれ角の最大値を 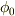 とすると,エネルギー保存より,
とすると,エネルギー保存より,
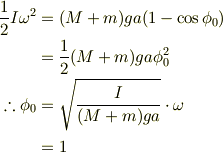
となってしまったのですが,これはやはり間違っていますか?
答えは, 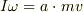 をもちいて,
をもちいて,  を消去してvを用いたものになっていました.
を消去してvを用いたものになっていました.
Re: 慣性能率
ミュフ猫 さんのレス (2010/02/03(Wed) 19:07)
横レス,失礼します.
φもωも時間tの関数では? おそらく,vが含まれるであろう初期条件の方程式を見落としているのでは? 間違ってたら,すみません.m(_ _)m
Re: 慣性能率
Yokkun さんのレス (2010/02/03(Wed) 19:40)
横レスNo.2です.
 は振動の角振動数を表そうとされているのだと思いますが,これと
は振動の角振動数を表そうとされているのだと思いますが,これと 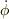 とは全く異なるものです.これを同一視されているのがそもそもの間違いだと思います.運動エネルギーは,
とは全く異なるものです.これを同一視されているのがそもそもの間違いだと思います.運動エネルギーは,
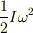 ではなく,
ではなく,
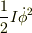 ですよね?この場合単振動ではありませんが,もし単振動の場合は
ですよね?この場合単振動ではありませんが,もし単振動の場合は

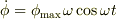 ということになると思います.
ということになると思います.
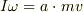
この  は
は 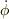 (の初期値)の意味です.回転軸周りにトルクの作用・反作用を及ぼしあったので,系としての角運動量保存を用いたのでしょう.
(の初期値)の意味です.回転軸周りにトルクの作用・反作用を及ぼしあったので,系としての角運動量保存を用いたのでしょう.
Re: 慣性能率
asdf さんのレス (2010/02/03(Wed) 20:16)
では,自分の式の  は何を表しているのでしょうか?
周期は,
は何を表しているのでしょうか?
周期は, 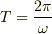 としたら,答えと一致しました.
としたら,答えと一致しました.
Re: 慣性能率
Yokkun さんのレス (2010/02/03(Wed) 20:41)
運動方程式から微小振動の周期を求めたところまでは合っているのでしょう.その  を
を 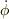 に転用されたところからあらぬ方向へといってしまいました.
に転用されたところからあらぬ方向へといってしまいました.
エネルギー保存を使うに当たってまず, 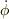 の初期値を求めることが先決なのです.その初期値を角運動量保存を使って求めるべきところを,全く異なる単振動の角振動数をうっかり使われてしまったわけです.
の初期値を求めることが先決なのです.その初期値を角運動量保存を使って求めるべきところを,全く異なる単振動の角振動数をうっかり使われてしまったわけです.
Re: 慣性能率
asdf さんのレス (2010/02/03(Wed) 22:15)
(No.26281のものです)と
の違いは何なのでしょうか?
前者は,単振動の角振動数,後者は,回転の角速度で,単位は,両者とも 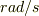 になると思うのですが・・・
になると思うのですが・・・
Re: 慣性能率
Yokkun さんのレス (2010/02/04(Thu) 00:34)
簡単のため,単振子の微小振動を例にとりましょう.
運動方程式は
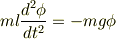
単振動一般の加速度
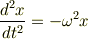
と比較して,
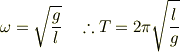
となります.asdfさんもこの流れを正しくたどられました.問題はその後です.
上の結果から,初期条件を例えば
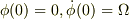
にとりますと,
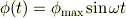
と書けることになりますが,ここでエネルギー保存
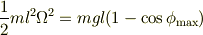
により,振幅 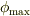 が決まるのです.
が決まるのです.
asdfさんは,上の議論における
角振動数  (
( 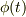 の振動を正射影とする円運動の角速度)
の振動を正射影とする円運動の角速度)
と
変位角の角速度 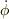 またはその初期値
またはその初期値 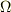
とを混同されているのです.
Re: 慣性能率
asdf さんのレス (2010/02/04(Thu) 03:59)
ありがとうございました. 分かりました.
Re: 慣性能率
ミュフ猫 さんのレス (2010/02/04(Thu) 09:21)
なるほど,そういうことでしたか・・・. Yokkunさん,ありがとうございます. 回答するにも,時にはエスパー能力が必要ですね.w