電磁気と相対論
電磁気と相対論
たまご さんの書込 (2010/02/01(Mon) 19:51)
問題が少し長いですが,お願いします. 今大学2年で電磁気を勉強しているのですが, 相対論の知識が必要な問題にあたりましてとき方がわからず こまっています. 解き方だけでもおねがいします.
電流が流れている導線の近くを電荷qをもつ粒子が座標系S1において, 速さvでx軸正方向へ運動している. また,座標系S1では導線の外側では電場が存在していないとする. このとき粒子に働く力について考える. 以下の問いに答えよ.
(1)座標系Sでの導線中の正電荷の電荷線密度λ=λ1とする. この正電荷の電気密度を電荷qとともに働く座標系S2(つまり, S1に対して,速度vで動いている.)から見るとどうなるか. S2での線電荷密度λ2を求めよ.
(2)次にS2での導線中の電子の電荷密度について考える.実は, 電子はS系で速度を持っているので導線中の電子の静止系S(rest)での 電荷密度とは異なっている.S系では導線の外側には電荷が存在しないので 単位長さあたりの正味の電荷量は0である.よって,S系での電子の 電荷線密度は−λ1となる. 電子の静止系での電荷線密度を−λ(rest)とするとき, λ1とλ(rest)との間の関係を求めよ.ただし,S系での電子の 速度をbとせよ.そしてさらに,S2系からみた電子の電荷線密度 を求めよ.ただし,S2系からみた電子の速度をdとせよ.
(3)S2系から見た導線中の電子の速度eをA(=v/c), B(=b/c)で表せ.そして,このeを用いて定義された D=1/√{1-(e/c)^2}をB,Dを用いて表せ.
(4)S2系での正電荷と負電荷(電子)を合わせた導線単位長さあたりの正味 の電荷密度Xをもとめ,これが0にならないことを示せ.
(5)(4)で示した通り,S2系では導線長さあたりの正味の電荷密度 が0にならない.これはS2系から見ると導線の外側に電場が生じる ことを意味する.S2での導線から距離r離れた場所での電場Eの 大きさと方向を求め,この電場により導線からの距離rの ところ(S2では静止している)電荷Qに働く力を求めよ.
(6)S2系での力をSで見たらどのように見えるか求め,Sではこの力は ローレンツ力に対応することを示せ.(導線に流れる電流が I=−λ1Bcと書け,電流Iの外側には磁場μI/2πrが生じる ここでμは光速cとεとの間にc^2=1/(εμ)の関係がある 係数である.)
Re: 電磁気と相対論
Yokkun さんのレス (2010/02/02(Tue) 19:07)
冗長な文字の置き換えがあって,ややこしいですね.導線(電流)は  軸方向でよいのでしょうか?
軸方向でよいのでしょうか?
速度  をもつ物体は,いわゆるローレンツ短縮によって
をもつ物体は,いわゆるローレンツ短縮によって  の方向に縮んで見えるのでしたね?導線は
の方向に縮んで見えるのでしたね?導線は 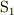 系において静止しているのですから,
系において静止しているのですから, 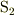 系から見ると
系から見ると 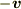 の速度で運動しています.すると,導線は縮んで観測されるため電荷密度はその分大きくなります.(1),(2)はこれでクリアできますか?
の速度で運動しています.すると,導線は縮んで観測されるため電荷密度はその分大きくなります.(1),(2)はこれでクリアできますか?
Re: 電磁気と相対論
たまごのたまご さんのレス (2010/02/03(Wed) 01:40)
できれば全て教えて下さい. 解説お願いします.
Re: 電磁気と相対論
Yokkun さんのレス (2010/02/03(Wed) 11:43)
系において導線の長さ
の部分を考えます.この部分の正電荷を
とすると線電荷密度は
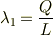
となりますね?これを 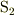 系から見ると,速度
系から見ると,速度 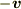 で動いていますから,長さが
で動いていますから,長さが
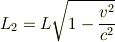
に縮んで見えることになります.すると, 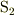 系から見た線電荷密度は,
系から見た線電荷密度は,
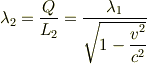
となると思いますが,いかがですか?
Re: 電磁気と相対論
ミュフ猫 さんのレス (2010/02/05(Fri) 20:52)
S系とS1系の違いって何だろうか・・・.
Re: 電磁気と相対論
Yokkun さんのレス (2010/02/05(Fri) 22:36)
>S系とS1系の違いって何だろうか・・・.
表記ミスでしょうね.1が抜けただけ.>ミュフ猫さん
(2)は,(1)と全く同じ問題です.
- S1で静止している正電荷(λ1)が,S2では速さvで動いている(λ2).
(2) S(rest)で静止している電子(-λ(rest))が,S1では速さbで動いている(-λ1). S(rest)で静止している電子(-λ(rest))が,S2では速さdで動いている.
いかがでしょうか?速さが違うだけで,成立する式の形は全く同じです.
Re: 電磁気と相対論
たまごのたまご さんのレス (2010/02/06(Sat) 20:34)
(2)はできました.ローレンツ変換をつかい,λrest*1/γとγλrestです. (3)がわからないです.
Re: 電磁気と相対論
Yokkun さんのレス (2010/02/06(Sat) 21:17)
γ因子がそれぞれ違うので気をつけてくださいね.どちらもγλ(rest)の形になるはずです.
(3)の前半は(2)で終わってます.
後半は,速度の合成側を用います.「速度e」と問われているので,定義された方向により負号が必要かもしれませんが,基本的にeはbとvの合成になります.
ここまでが,数学的準備.(4)から本題ですが,ここまでクリアすればあとは一直線です.
Re: 電磁気と相対論
たまごのたまご さんのレス (2010/02/06(Sat) 23:29)
γ'e やVe'を使ったので,解き方がわかりません. 具体的に解き方をきいているのですが?
Re: 電磁気と相対論
Yokkun さんのレス (2010/02/06(Sat) 23:36)
(2)は大丈夫ですか?不安であれば(2)の結果を書いてみてください.ここが理解されてないと(3)には進めないと思いますので.
(3)ですが,ガリレイ変換のレベルでは, 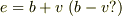 になっていませんか?これを相対論の合成則で書いてください.それができたら,
になっていませんか?これを相対論の合成則で書いてください.それができたら, 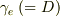 に代入・整理します.すると,その中に
に代入・整理します.すると,その中に 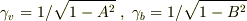 が姿を現します.
が姿を現します.
あ,ちなみに 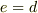 は同じものですよね?
は同じものですよね?
Re: 電磁気と相対論
たまご さんのレス (2010/02/07(Sun) 05:22)
(2)は解けました.
ちなみに,
-λ1=λ(rest)/√(1−b^2/c)
-λ2=λ(rest)/√(1-d^2/c)となりました.
(3)なのですが,ガリレオ変換で考えるとd=b+vはわかりますが,
速度dを相対論の合成測を使って解く方法がわかりません.
ここは基本かもしれませんが,まだ大学二年なもので
相対論=光速度不変って程度にしか相対論を知らないので・・・(><:)
詳しく教えてもらえませんか?
Re: 電磁気と相対論
Yokkun さんのレス (2010/02/07(Sun) 08:21)
一般に,S系に対して速度vをもつS'系において,vと同じ方向に運動する物体の速度がuであるとき,S系にもどって観測される速度は,
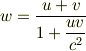
となります.ローレンツ短縮,時間の遅れ,同時の相対性,ローレンツ変換,速度の合成・・・あたりまでの相対論の基礎については,あらためて学ばれるとよいかと思います.
Re: 電磁気と相対論
たまごのたまご さんのレス (2010/02/07(Sun) 14:49)
S系とS'系ではvで動きながら見ている分違います.
(3)は(2)ででてくるのがよくわかりません.(2)ではve',γ'をつかったので出てきませんでした.
Re: 電磁気と相対論
たまご さんのレス (2010/02/07(Sun) 15:37)
(3)の式の整理に苦しんでいます^^:
まずd=b+v/1+{bv/c}^2
=c^2b+c^2v/c^2+bv
また,b+v=c(A+B),c^2+bv=c^2(1+AB)より,
よって求めるdは
=c(A+B)/c^2(1+AB)になりました.(←ちなみに,あってますか?)
また,求めるDは
=1/√{1-(b/c)^2}にさっきの結果を代入すると,
1/√[1-{A+B/c(1+AB)}^2]
までは整理できたのですが,この後の整理法がわかりません.
よろしくお願いします.
ちなみにS=S1系です.間違いすみません.
Re: 電磁気と相対論
Yokkun さんのレス (2010/02/07(Sun) 16:14)
dは速さですが,次元が違ってます.cのつくところがおかしいですね. Dも無次元の量ですから,やはりcが違ってます. また,分母,分子が多項式のとき()でくくらないと全く意味不明の式になりますので注意してください.
Dの計算は,まず分母のルートの中を通分して因数分解し,全体をルートに入った分数の形に整理しましょう. 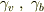 が姿を現すはず.
が姿を現すはず.
Re: 電磁気と相対論
ミュフ猫 さんのレス (2010/02/07(Sun) 16:18)
たまご氏とたまごのたまご氏は同一人物だろうか・・・.
Re: 電磁気と相対論
たまご さんのレス (2010/02/07(Sun) 16:28)
あのう,dは,さっき教えてもらった
w=u+v/1+uv/c^2を使って,
d=b+v/1+bv/c^2としてはいけないのですか?
ちなみに,俺はたまごですが,たまごのたまごさんでは
ありませんよ{^^}
Re: 電磁気と相対論
たまご さんのレス (2010/02/07(Sun) 19:03)
はい.マジで別人ですよ!
1-d^2/c^2
=1-1/c^2・(b+v)^2/{1+(bv/c^2)}^2
=1-(b+v)^2・/{c^2+2bv+(bv/c^2)^2}
の後の整理の仕方がどう考えてもひらめきません><
どうやって,因子を導き出すのでしょうか?
Re: 電磁気と相対論
たまご さんのレス (2010/02/07(Sun) 20:18)
yokkunさん,親切にありがとうございます.
結果を聞いてからもう一度自分で展開して整理してみたら
普通にできました.
結果は,
==1-1/c^2・(b+v)^2/{1+(bv/c^2)}^2
={1/γ^2(v)γ^2(e)}{1/(1+AB)} となりました.
また,(4)の電荷密度は
(1)と同様に考えて,
Dλ(rest)であっていますか?
また,正味の電荷密度が0にならないことを
示す方法がひらめきません.
何度も質問をしていてすみませんが><
よろしくお願いします.
Re: 電磁気と相対論
Yokkun さんのレス (2010/02/07(Sun) 20:57)
(1)でS2から見た正電荷の密度を求めましたから,(3)で求めたS2から見た負電荷の密度と一緒にして,正味の電荷密度を求めればよいのです.その上で,λ(rest)を通じて,λ1で表してください.そうすることで,ガウスの法則によるS2での電場の導出を経て,S1で観測されている電流I=λ1bとの関係を導出できることになります.
Re: 電磁気と相対論
たまご さんのレス (2010/02/07(Sun) 22:06)
たぶん(4)の途中まで解けました.
求めたいはλ=γλ1(1+D)となりました.
あとはゼロにならないことを示す方なのですが,
ガウスの法則を使ってS2系での電場Eを表すと,
∫S{E・n}ds=1/ε∫vλdvとなると思うのですが,
この後上の式をどのように計算していけばいいですか?
0ではないと証明する方法が浮かびません><:
Re: 電磁気と相対論
Yokkun さんのレス (2010/02/07(Sun) 22:15)
ガウスの法則は,まだですね.ゼロでないことを示すのは何も必要ありません.ゼロでない結果を求めるだけです.ちなみに,結果は
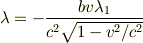
となると思います.これを用いて,(5)の電場を求めるのにガウスの法則を使うわけです.もっとも,線分布電荷による電場を公式として把握されているのならそれでよいのですが.
Re: 電磁気と相対論
たまご さんのレス (2010/02/07(Sun) 22:28)
すみませんがλの結果の導出も教えてもらえないでしょうか?
あと,I=λ1bの関係?もさっぱりわからないのでこちらも,
少し説明をできたらよろしくお願いします.
てか,なんか聞いてばっかですみません.
本来は,もっと自分で考えるべきなのですが,この問題が明日の昼のテストで
出るらしいので(先生が100点を取らせないために?),
早く解き方を一通り理解したかったもので・・・><:
Re: 電磁気と相対論
ミュフ猫 さんのレス (2010/02/07(Sun) 23:45)
岩波書店「ファインマン物理学?・電磁気学」(宮島龍興訳)
第13章静磁場 13−6電磁場の相対性
↑ ここに詳しく載ってます.もう時間が無いので, 明日の午前中にでも,図書館で調べてみては?
Re: 電磁気と相対論
なんとなく さんのレス (2010/02/08(Mon) 00:12)
蛇足ですが,以下のところにも詳細な説明があります.
www.geocities.jp/mtsugi04/re6.PDF
PDFが読めるなら,参考にしてください.
Re: 電磁気と相対論
たまごのたまご さんのレス (2010/02/08(Mon) 01:06)
たまごさん,佐大ですか?
Re: 電磁気と相対論
たまごのたまご さんのレス (2010/02/08(Mon) 01:52)
今学校でレポートしてるけどなかなか終わらんですね(-.-;) 終わりました?
Re: 電磁気と相対論
たまごのたまご さんのレス (2010/02/08(Mon) 02:45)
結局何番までできた?
Re: 電磁気と相対論
たまごのたまご さんのレス (2010/02/08(Mon) 08:50)
(2)までであとがわからん感じ(-.-;) 今日のテスト休んだ人だけよね?
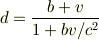
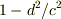 を計算してみたらいかがでしょう.
を計算してみたらいかがでしょう.