重積分

重積分

asdf さんの書込 (2010/01/31(Sun) 20:32)

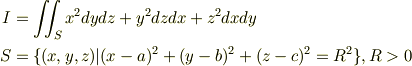
I&=\iint_S x^2dydz+y^2dzdx+z^2dxdy\\S&=\{(x,y,z)|(x-a)^2+(y-b)^2+(z-c)^2=R^2\}, R>0

で，Iを求めよ．

という問題です．

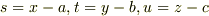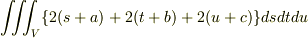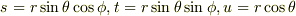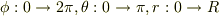まず， s=x-a,t=y-b,u=z-c とおき，Iに代入して，ストークスの定理を用いて， \iiint_V\{2(s+a)+2(t+b)+2(u+c)\}dsdtdu とし， s=r\sin\theta\cos\phi,t=r\sin\theta\sin\phi,u=r\cos\theta と変数変換をして求めようと思ったのですが，どうしても計算が合いません． ( \phi:0 \to 2\pi, \theta:0 \to \pi, r:0 \to R )

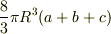答えは， \frac{8}{3}\pi R^3(a+b+c) です．

やり方が間違っているのでしょうか？それとも計算ミスでしょうか． ご教授お願いします．

Re: 重積分

山旅人 さんのレス (2010/01/31(Sun) 21:16)

> それとも計算ミスでしょうか． ええ，そのようですね．

与式＝2∫ v (s＋t＋u)dsdtdu＋2(a＋b＋c)∫ v dsdtdu ← ここまで OK． 第１項は対称性により 0，第２項の積分部分は半径 R の球の体積．よって 「答え」の結果を得ます．（ストークスの定理ではなく，ガウスの定理ですね）

Re: 重積分

asdf さんのレス (2010/01/31(Sun) 22:19)

ありがとうございます． 本当ですね．打ちミスっていました． ガウスの定理ですね．

なぜ，第一項が対称性により０になるのでしょうか？

Re: 重積分

山旅人 さんのレス (2010/01/31(Sun) 22:33)

> なぜ，第一項が対称性により０になるのでしょうか？

V：{(s，t，u)|s 2 ＋t 2 ＋u 2 ≦R 2 } は，原点中心，半径 R の球の表面及び内部ですから， (s 0 ，t 0 ，u 0 )∈V のとき (−s 0 ，−t 0 ，−u 0 )∈V ですね．よって足し合わせれば 0 になります．

Re: 重積分

asdf さんのレス (2010/01/31(Sun) 22:43)

なるほど．本当はこんなにも簡単に計算できるんですね． 一応，もう一度極座標においてやってみたら確かに０になりました．

ありがとうございました．