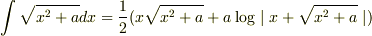積分公式

積分公式

asdf さんの書込 (2010/01/31(Sun) 00:28)

\int \sqrt{x^2+a} dx = \frac{1}{2}(x\sqrt{x^2+a}+a\log\mid x+\sqrt{x^2+a} \mid)

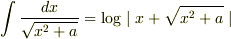
\int \frac{dx}{\sqrt{x^2+a}} = \log \mid x+\sqrt{x^2+a} \mid

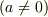
(a\neq0)

の二つの公式の導出（左辺から右辺）はどうすればよいのでしょうか． 部分積分を用いてやってみたのですが，違う答えが出てきてしまいました．

Re: 積分公式

山旅人 さんのレス (2010/01/31(Sun) 16:23)

x＋√(x 2 ＋a)＝uとおくと，√(x 2 ＋a)＝(u＋a/u)/2，dx＝(1/2)(1＋a/u 2 )du 最もオーソドックスな方法です．以下，ご自分で．

Re: 積分公式

asdf さんのレス (2010/01/31(Sun) 20:17)

なるほど．置換積分をすればよかったんですか． ありがとうございました．導けました．

Re: 積分公式

anon さんのレス (2010/02/01(Mon) 19:03)

解決したようでよかったですが，ひとつ気になったので．

> 違う答えが出てきてしまいました

とのことですが， 一件違う形に見えても不定積分としてはどちらも正しい， ということはよくあります． 例えば，log(x/(x+1)) は -log(1+1/x) と同じですし， 不定積分が log(3x^2) となるような場合は 2log x としてもよいわけです．

答え合わせをして違っているようだったら 自分のやった計算を全部ご破算にしてしまう， そういう学生は多いですね． でも，本当に間違っていたとしても どこが違っていたのかを突き止めれば 自分がどんな思い違いをしていたのかわかりますし， 本当は間違っていなくてうまく変形すれば実は同じものだったとしても その変形の道筋を突き止めればやはり理解が深まります． せっかくやった計算をあっさり捨ててしまうのはもったいないことです．

とくにasdfさんに宛てたわけではなく， ここを利用している学生さんたちに気に留めてほしいこととして書き綴りました．