体積

asdf さんの書込 (2010/01/30(Sat) 05:29)

大学１回生です．

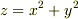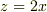曲面 z=x^2+y^2 と平面 z=2x に囲まれた部分の体積を求めよ．という問題です．

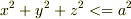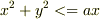例えば， x^2+y^2+z^2<=a^2 と x^2+y^2<=ax の共通部分の体積は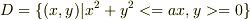， $D=\{(x,y)|x^2+y^2<=ax,y>=0\}$ とおいたらよいというのはわかるんですが，今回の問題は，図もあまりイメージできなく，Dをどうすればよいかわかりません．

どうすれば体積を求められるのでしょうか．

答えは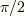， $\pi/2$ です．

曲面 z＝x ² ＋y ² …(1)は z 軸を回転軸とする回転放物面，平面 z＝2x …(2)は，yz 平面を y 軸の回りに x 軸方向に傾けた平面です．

両者に囲まれた部分を y 軸に垂直な平面 y＝k …(3) で切った断面は，放物線 z＝x ² ＋k ² …(4)，直線 z＝2x …(5) で，(4)(5)で囲まれた弓形の面積は 4(1−k ² ) ^3/2 /3 …(6)

(6)を k について −1 〜 1 で積分すれば π/2 が得られます．

分かりました．ありがとうございました．