DOG さんの書込 (2010/01/23(Sat) 20:04)

下のURLに問いの図をアップしています．

• http://imagepot.net/view/126424400858.jpg

図のときの，光路差を求める問題なのですが，

格子面を通り抜けた後の空気中における光路差は，dsinθ 格子面を通り抜けた前の空気中における光路差，dsinφ

であるから，全体としての光路差は d(sinθ-sinφ) の絶対値だと思ったのですが．

答えは，d(sinθ+sinφ) でした．

どうして引いているのではなく，足しているのでしょうか．

DOG さんのレス (2010/01/23(Sat) 20:29)

先ほどの続きで，

例えば下のURLの画像の問い

• http://imagepot.net/view/126424597998.jpg

では，光路差どうしを引いています．

これと上との違いが分からないのです．

どなたか教えていただけないでしょうか．

Yokkun さんのレス (2010/01/23(Sat) 20:57)

２つの光路で，どちらが長いのかよく比べてみてください．

初めの例では，一方が入射前後でいずれも長くなっています． 次の例では，入射前後で長い方が入れ替わっていますよね？

MIROｓ さんのレス (2010/01/23(Sat) 20:59)

というのは，線の間隔つまり格子定数のことでしょうか？

とりあえず，格子面を透過する前の空気中における光路差が

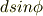
格子面を透過した後の空気中における光路差が

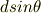
ならば隣り合うスリットを透過する光における「全体としての」光路差は，差をとるのではなく， その光路差を足し合わせないと「全体としての」光路差にはなりません．

ちなみに，ある任意のスリットを 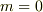として，そこから 番目のスリットとの「全体としての」光路差は， を波長として，

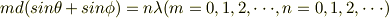
と，なります．

DOG さんのレス (2010/01/23(Sat) 21:25)

YokkunさんMIROsさん，迅速な返答ありがとうございます．

Yokkunさんに質問なのですが，「長い」というのは何が長いということなのでしょうか？

ごめんなさい，まずそこからよく分からないです・・・・

Yokkun さんのレス (2010/01/23(Sat) 22:53)

>「長い」というのは何が長いということなのでしょうか？

もちろん，光路長のことです．光が進む経路の長さ，さらに発展的には光学的距離です．２つの経路を進んだ光の経路差によって強めあったり弱めあったりの干渉条件が決まるのですよね？反射で位相が変わらなければ（山谷逆転が起こらなければ），経路の差が波長の整数倍なら強め合い，半波長あまれば弱めあうということになるのでした．

DOG さんのレス (2010/01/24(Sun) 00:43)

なるほど． 干渉条件については把握しております．

そこでもう一つ質問があるのですが，

その入射前後で光路長が長くなっているのかいないのかで 光路差どうしを足すのか引くのかということをいままで考えたことがなかったので，そもそもなぜそこから考えるのかが分かりません・・・・・

根本的な理解に欠けているのかもしれません・・・・

図々しいですが，もう少し詳しく教えていただけますでしょうか．

Yokkun さんのレス (2010/01/24(Sun) 01:58)

初歩的には，入射前から時間経過にそって追跡されるのがよいと思います．入射光線において，波面は射線（進行方向）に垂直です．回折格子の干渉の場合位相がそろった光を利用しますから，２つのとなりあう射線に対して，垂直にならぶ位置が同じ位相で通過する点になります．斜め入射では，入射点において位相がずれることになりますね？

ご紹介のはじめの問題では，下の光路ほど入射前後で遠回りになっています．入射前の同じ波面は，下にいくほどおくれて回折格子に入っていますね？そして，回折格子の内部では距離が等しいので，ずれはそのまま保存されます．さらに出て行くときに，与えられた図の方向への光路は，射線に垂直な位置の位相のずれがさらに拡大しているのがおわかりでしょう？回折が起こったあとの２つの射線は垂直位置に同位相の波面がならんではいないわけです．

つまり，斜め入射で格子面に垂直な方向に対する射線の角度（入射角）の向きと出て行く斜線の屈折角の向きが逆の場合，経路差は当然前後の経路差の足し算になり，同じ場合は前後の経路差の引き算になるわけです．

DOG さんのレス (2010/01/24(Sun) 11:03)

二段落目までは理解できました． しかし三段落目の「つまり〜」からがどうもピンときません・・・

そもそも角度の向きとはどういうことなのでしょうか？

入射角の向きと出て行く斜線の屈折角の向きが逆⇒経路差は前後の経路差の足し算

入射角の向きと出て行く斜線の屈折角の向きが同じ⇒経路差は前後の経路差の引き算

という理屈が，どうしても分かりません．

なかなか文字で伝えるのは難しいと分かっておりますが，もう一度そこのところの解説をお願いできませんか?

ミュフ猫 さんのレス (2010/01/24(Sun) 13:01)

横レス失礼します．

結局，被写体から観測者（目ん玉）までの「光路長」が隣り合う光線間で， どのように異なるかを理解できていないのでは？

「ミクロ的に，被写体も観測者も光線に対して垂直な表面を持つ」

と仮定した上で，光路長を比較すれば，足し算になるか引き算になるかが， 幾何学的にイメージできるかも．

• http://imagepot.net/view/126424400858.jpg においては，

反射点に辿り着くまでも，折り返した後も，一方の光線のみがより長く進む．

• http://imagepot.net/view/126424597998.jpg においては，

反射点に辿り着くまでは一方の光線が，折り返した後は別の方の光線がより長く進む．

Yokkun さんのレス (2010/01/24(Sun) 16:37)

ミュフ猫さん，バックアップありがとうございます．

>そもそも角度の向きとはどういうことなのでしょうか？

ここでは，図で格子面に垂直な方向に対して時計回りか反時計回りかというつもりでそう表現しました．入射角が時計回りの角度のとき，図で下の経路の方が遠回り．出て行く射線は反時計回りなので，やはり下の経路が遠回りです．もちろん遠回りであることはごちゃごちゃいわずとも図を見れば明らかです．光になったつもりでしっかりたどってみてくださいね．

DOG さんのレス (2010/01/24(Sun) 18:10)

ミュフ猫さん，補足説明ありがとうございます． Yokkunさんにも自分の疑問点に忠実に答えていただき，感謝しています．

最初の画像において，なぜ光路差どうしを足すのかというのはちゃんとイメージがわきました．

そこで二枚目のほうなのですが，たしかに， 「反射点に辿り着くまでは一方の光線が，折り返した後は別の方の光線がより長く進む」

というのは理解できます．

しかし今になっていろいろ考えてしまって，二枚目の画像においても，結局光路差どうしなのだから，それらを足した中で波長が整数個あっても強めあうのではないかという疑問が出てきました・・・・

なぜ，'遠回り'が隣り合う光線どうしで起こったら，「引く」ということになるのでしょうか？

本当にしつこくて申し訳ないです・・・・

Yokkun さんのレス (2010/01/24(Sun) 18:54)

>結局光路差どうしなのだから，それらを足した中で波長が整数個あっても強めあうのではないか

それぞれの場所で生じた光路差が，それぞれに波長の整数倍であれば・・・ということでしょうか？足した結果（引いた結果）がようやく波長の整数倍になるということの方が普通ですよね？何箇所かで生じた光路差はすべて「足さなくては」なりません．他方が短かったらマイナスの「差」を足すんです．おわかりでしょうか？もっと単純に考えてください．要は２つの経路をたどる光の一方が「山」でゴールにたどりついたときに，もう一方はどういう変位で同時にたどりついているかを判断するのですから，ただ，光にとっての２つの道筋の長さの差を評価すればいいわけです．

DOG さんのレス (2010/01/24(Sun) 21:12)

頭をやわらかくして考えてみると，だんだんと仰っていることの意味が分かるようになってきました．

昨日とはうってかわって，多くの疑問が解けました！

本当にYokkunさんにはお世話になりました．

これでまた道が開けてきました． 本当にありがとうございました．