ハミルトニアン
ハミルトニアン
トビラ.. さんの書込 (2010/01/21(Thu) 00:15)
こんばんわ.すみません,本読んでてわからない数式があったのですが,どなたか教えてください.
ハミルトニアン 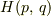 とエネルギー
とエネルギー  の間には
の間には 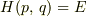 の関係があるとして,
の関係があるとして, 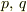 はその正準変数,つまりは,
はその正準変数,つまりは,  の正準共役な量を
の正準共役な量を 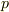 とします.また,
とします.また, 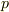 は
は 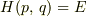 をといた関数です.
すると本では
をといた関数です.
すると本では
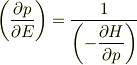
が成立する.と書いてあるのですが,どうして右辺の分母の符号がマイナスになるのでしょうか? どなたかアドバイスお願いします.
Re: ハミルトニアン
名無しさん さんのレス (2010/01/21(Thu) 17:30)
こんにちは.
簡単に説明してしまいます.「ディメンション」を考えてみると良いでしょう.
たとえば, 式(1)
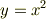
という数式があったとします.
これと同じようにして,次の場合も同じになります. 式(2)
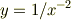
さて微分の定義から明らかなように・・・ 後の式に変形したとき.そのディメンションに含まれる数が表に出ます.
そのため,マイナスがつきます.
Re: ハミルトニアン
yama さんのレス (2010/01/21(Thu) 22:29)
その関係式が本当に成り立つかどうか疑問に思います. 例えば簡単な場合として
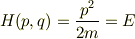
のときは
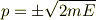
なので
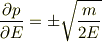
であり,また
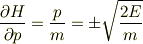
となるので
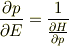
という関係が成り立ち,マイナスの符号はつかないと思うのですが.
Re: ハミルトニアン
yt さんのレス (2010/01/22(Fri) 02:53)
私もマイナスの符号はつかないと思います.その本の誤植ではないでしょうか.
とりあえず全微分の形式で書くと判り易いと思います.
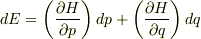 左辺に
左辺に 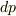 が来るように式変形すると,
が来るように式変形すると,
 となるので,
となるので, 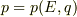 について,
について,
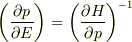
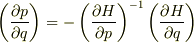 の関係がある事が判ります.
の関係がある事が判ります.
Re: ハミルトニアン
トビラ.. さんのレス (2010/01/22(Fri) 11:40)
みなさんありがとうございます.名無しさん申し訳ありませんが,僕の知能では理解できませんでした.すみません.
もう少し詳細にこの本に乗っていることを書いてみます.この本では一般化された断熱不変量 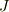 の計算(証明)をしているんです.
まず,
の計算(証明)をしているんです.
まず, 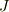 を
を 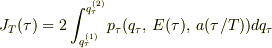 で定義されます.
このとき
で定義されます.
このとき 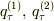 は
は 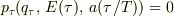 の2つの根です.
「
の2つの根です.
「  が時間
が時間  とともに十分ゆっくりと変化するときは
とともに十分ゆっくりと変化するときは 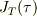 の値は
の値は  が変わっても変化しない」という一般的な断熱不変量の証明が目的なんですけども,その計算の過程で,
が変わっても変化しない」という一般的な断熱不変量の証明が目的なんですけども,その計算の過程で,
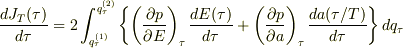 が得られ,
が得られ, 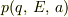 は
は 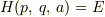 を
を 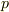 について解いてえられた関数なので,
について解いてえられた関数なので,
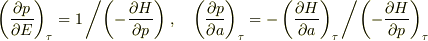 が成立する.これらの関数と,
が成立する.これらの関数と, 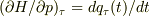 を用いると結局
を用いると結局
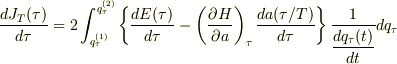
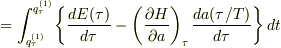 となる.って書いてあるんですが,この後もこの右辺の第2項の計算はマイナスのまま進んでいます.これを理解するには,最初にした僕の質問を理解すれば後も同様に計算できるだろうと憶測したため,あの質問をしました.
※朝永振一郎著「量子力学I(第2版)」109ページ引用しました.
となる.って書いてあるんですが,この後もこの右辺の第2項の計算はマイナスのまま進んでいます.これを理解するには,最初にした僕の質問を理解すれば後も同様に計算できるだろうと憶測したため,あの質問をしました.
※朝永振一郎著「量子力学I(第2版)」109ページ引用しました.
Re: ハミルトニアン
yama さんのレス (2010/01/22(Fri) 14:15)
マイナスがないものとして計算されているように見えますが.
つまり 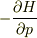 のマイナス符号をとったほうがその後の計算と合致するようですが.
のマイナス符号をとったほうがその後の計算と合致するようですが.