ばねがする仕事

ばねがする仕事

初心者ですみません さんの書込 (2010/01/20(Wed) 17:21)

ばねがする仕事についての質問です． ばねが伸びる方向に座標軸をとるとき， ばねを自然長からｘ（ｍ）伸ばしたときのばねがする仕事Wは， フックの法則より，弾性力F＝-ｋｘ（N)がばねに蓄えられるので， W＝∫（０→ｘ）（−ｋｘ）ｄｘ 逆にｘ（ｍ）縮めたときは， 弾性力F＝ｋｘ（N)がばねに蓄えられるので， W＝∫（ｘ→０）ｋｘｄｘ として考えたのですが，いずれも仕事Wが負になってしまいます． これは座標の取り方が悪いのでしょうか？

よろしくお願いします．

Re: ばねがする仕事

Yokkun さんのレス (2010/01/20(Wed) 17:57)

「弾性力が蓄えられる」という表現はあまり使われません．蓄えられるといえば位置エネルギーですね．

自然長から x 伸ばしたときにばねがする仕事

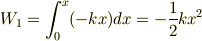
W_1 = \int_0^x (-kx)dx = -\frac{1}{2}kx^2

ただし， x 軸は伸びる方向．これはＯＫ．

自然長から x 縮めたときにばねがする仕事

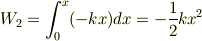
W_2 = \int_0^x(-kx)dx = -\frac{1}{2}kx^2

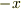ただし， x 軸は縮む方向．伸びる方向を x 軸にとるのならば， x を -x にとりかえればいいでしょう．どちらもエネルギーが蓄えられるので仕事はマイナスで同じですね？ばねにとってはマイナスの支出をしたからエネルギーが増えたのです．

もし， x 伸びている所から自然長に戻すという意味であれば，

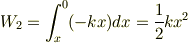
W_2 = \int_x^0(-kx)dx = \frac{1}{2}kx^2

力の方向は伸ばすときと変わりません．力の方向と移動の方向が同じなので仕事はプラスになります．ばねにとっては，プラスの支出．位置エネルギーが減少してゼロになりました，ということです．

Re: ばねがする仕事

初心者ですみません さんのレス (2010/01/21(Thu) 12:56)

返答ありがとうございます． F＝−ｋｘという式がいまいちわかりません． ばねが伸びる方向に座標軸をとるとき，

変位ｘ＜０ならばF＝−ｋｘ 変位ｘ＞０ならばF＝ｋｘ つまり，F＝ｋｌｘｌ ｌｌ：絶対値 ということなのでしょうか？

Re: ばねがする仕事

Yokkun さんのレス (2010/01/21(Thu) 22:06)

>変位ｘ＜０ならばF＝−ｋｘ >変位ｘ＞０ならばF＝ｋｘ

変位ｘ＜０ならばF＝−ｋｘ 変位ｘ＞０でもF＝−ｋｘ

なのです．力はベクトルで，x軸方向の場合 F>0，逆の場合 F<0 ですね？

x<0 のとき，F=-kx >0 x>0 のとき，F=-kx <0

というわけです．

Re: ばねがする仕事

初心者ですみません さんのレス (2010/01/22(Fri) 17:38)

分かりやすい解説ありがとうございました！