線形　大学１回

yjddj さんの書込 (2010/01/18(Mon) 00:41)

実数全体で定義された実数値連続関数全体からなるベクトル空間の中で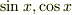， $\sin x,\cos x$ は１次独立であることを示せ

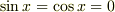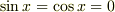という問題で， $\sin x=\cos x=0$ をみたすxが存在しないことから明らかですが，うまく説明することができません．どう書けばよいでしょうか．

> $\sin x=\cos x=0$ をみたすxが存在しないことから明らかこれ，違いますよね．

例えば，二つの定数関数 f(x)=1 と g(x)=2 について， f(x)=g(x)=0 となるような x は存在しませんが， f と g は一次独立（線形独立）ではありません．

独立性の定義をよく確認しましょう．

>> をみたすxが存在しないことから明らか >これ，違いますよね．

はい．違いますね．自分はいったい何を考えていたのでしょうか．

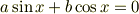
$a\sin x + b\cos x=0$

をみたすa,bが必ずa=b=0となることが条件ですよね．

わかりました．ありがとうございました．