分類の部分から自信が無くて困っています.
分類の部分から自信が無くて困っています.
時計 さんの書込 (2010/01/17(Sun) 14:01)
? 15N7?16 O(オー)8 ?39Ca20 ?40Ca20 ?53Cr24 ?75As33 ?141Pr59 ?155Gd64 ?171Yb70 ?207Pb82 ?231Pa91 ?260Rf104 について下の各問に答えよ. (1) 以上の原子核を,a) 二重閉核,b) 二重閉核±1核子,c) 近似的に成立する結合則によりO+となる原子核,d) 結合則によりO+以外のスピンやパリティーに決まる原子核に分類せよ. (2) 二重閉核の原子核のスピン,パリティーを書け. (3) 二重閉核±1核子の原子核,それぞれに対して,基底状態の波動関数,スピン・パリティー,磁気能率を求めよ. (4) 結合則によりO+以外のスピンやパリティーに決まる原子核,それぞれに対して,基底状態の波動関数,スピン・パリティー・磁気能率を決めている核子の準位,スピン・パリティー,磁気能率を求めよ. なお,原子核全体の波動関数はエネルギー準位に詰まった時の陽子及び中性子の個数で表す.例えば7Li3(A=7,Z=3)は陽子:(1s1/2)2(1p3/2)1中性子:(1s1/2)2(1p3/2)2で表す.あるいは,二重閉核を使って4He2(Z=2,N=2)⊗陽子:(1p3/2)1中性子:(1p3/2)2で表す. また,磁気能率は演算子μ= j[・j/(j2) g+s・j/(j2) gs] μNのz成分の期待値<j,m=j|μz|j,m=j>で与えられる.ここでg=1(陽子)=0(中性子) ,gs=gs(p)(陽子),=gs(n)(中性子)で,答えはμN,gs(p),gs(n)で表わせ.
以上です.分類できるものはやったのですが,上記のものがどうしても判りません.自分なりに(1)で分類したところ,
(1)(a)?,?(b)?,?(c)?(d)?,?,?,?,?,?,?
となりましたが,自信が無いです. (2)からはよく解らないので,教えていただけるとありがたいです. よろしくお願いします.
Re: 分類の部分から自信が無くて困っています.
mNeji さんのレス (2010/01/18(Mon) 14:14)
広範囲の問題ですね.全てにお応え出来ませんが,一部の考え方を書いて見ます.
原子では,その中心に位置し,正電荷の原子核の回りに陰電荷をもつ電子雲がクーロンの力により,緩やかに閉じ込められています.他方,原子核では,陽子と中性子が核力により,相互に密集して閉じ込められています.
状況が随分と違う割には,個々の粒子(電子とか核子)の運動が「平均的なポテンシャル」によって決められる為に,意外と似たエネルギー準位を持つのも面白いですね.電子とか核子は,電荷やアイソスピンを持つフェルミオンで,かつその多数系であることが,著しい特徴でしょうか.また,日常の物体運動と違って,回転孤立系の為に,軌道角運動量やスピン角運動量などが保存量であります.
# 他の保存量については,ttp://www.metro-u.ac.jp/~suzukitr/qma6.pdf#search=%27%E6%B3%A2%E5%8B%95%E9%96%A2%E6%95%B0%20%E3%83%91%E3%83%AA%E3%83%86%E3%82%A3%27などをご覧になると良いかもしれません.
とは言え,大きく違うこともあるので,そこらを考えて見ます.
電子では,(軌道)角運動量 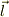 とスピン(角運動量)
とスピン(角運動量) 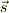 とは相互作用が小さくて,別々に保存される様ですが,核子では,軽い核を除き,所謂LS力,
とは相互作用が小さくて,別々に保存される様ですが,核子では,軽い核を除き,所謂LS力, 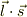 が大きいので,角運動量,
が大きいので,角運動量, 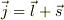 が良い保存量になります.
が良い保存量になります.
何れの場合も,同じ角運動量もつ粒子は,その射影成分に一つずつしかはいれないので,すべてが埋まった場合,全体の角運動量は,ゼロになります.また,このとき,空間の座標を反転しても波動関数が替われないのでパリティは正,すなわち閉殻, 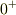 となります.
となります.
これで,(3),(4)や奇核,奇奇核などの論議は,他の識者の方々のご説明をお待ち下さい.
Re: 分類の部分から自信が無くて困っています.
時計 さんのレス (2010/02/03(Wed) 10:18)
>mNejiさん
返事がとても遅れてしまってすみません. 丁寧なご説明有難うございます! あの後なんとか自分なりに解いてみて解くことが出来ました. どうも有難うございました.