線形代数学

djwk さんの書込 (2010/01/16(Sat) 18:32)

大学１回です．

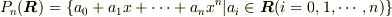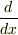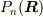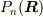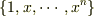高々n次の実係数多項式全体のなすR上のベクトル空間 $P_n(\bm{R})=\{a_0+a_1x+\cdots+a_nx^n|a_i\in\bm{R}(i=0,1,\cdots,n)\}$ を考える．微分 $\frac{d}{dx}$ は $P_n(\bm{R})$ の１次変換である． $P_n(\bm{R})$ の基底 $\{1,x,\cdots,x^n\}$ に関する

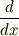
$\frac{d}{dx}$

の表現行列を求めよ．

という問題です．

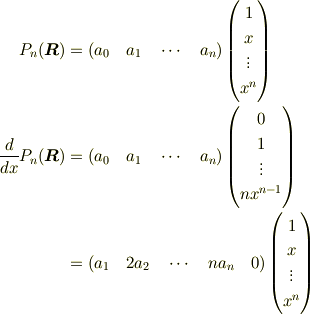
$P_n(\bm{R})&=(a_0 \quad a_1 \quad \cdots \quad a_n)\begin{pmatrix} 1 \\ x \\ \vdots \\ x^n \end{pmatrix}\\\frac{d}{dx}P_n(\bm{R})&=(a_0 \quad a_1 \quad \cdots \quad a_n)\begin{pmatrix} 0 \\ 1 \\ \vdots \\ nx^{n-1} \end{pmatrix}\\&=(a_1 \quad 2a_2 \quad \cdots \quad na_n \quad 0)\begin{pmatrix} 1 \\ x \\ \vdots \\ x^n \end{pmatrix}$

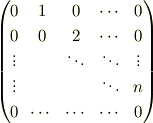
ゆえに，求める表現行列は，

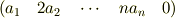
$(a_1 \quad 2a_2 \quad \cdots \quad na_n \quad 0)$

でよいでしょうか．それとも，まったく見当違いのことをやっているでしょうか．どなたかご教授よろしくお願いします．

Re: 線形代数学

djwk さんのレス (2010/01/16(Sat) 18:40)

すみません．列ベクトル中の...を縦にする方法があれば教えてください．

Re: 線形代数学

クロメルさんのレス (2010/01/16(Sat) 20:47)

確か，縦ドットはvdotsだったと思います． $\vdots$ ちなみに斜めは，ddotsです． $\ddots$ それぞれ，vertical（縦）diagonal（対角）の略ですね．

そして，本題ですが，ちょっと違うのですよ．例えば，三次の多項式だと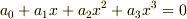， a_0+a_1x+a_2x^2+a_3x^3=0 微分すると，

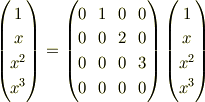
$\begin{pmatrix}1 \\x \\x^2 \\x^3 \\\end{pmatrix}=\begin{pmatrix}0 & 1 & 0 & 0 \\0 & 0 & 2 & 0 \\0 & 0 & 0 & 3 \\0 & 0 & 0 & 0\end{pmatrix}\begin{pmatrix}1 \\x \\x^2 \\x^3\end{pmatrix}$

ではないかなと思います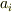． a_i を使わないのが気になりますが (^^;

Re: 線形代数学

djwk さんのレス (2010/01/16(Sat) 21:18)

vdotsですか．ありがとうございます．覚えておきます．

行列の式ですが，

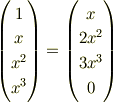
$\begin{pmatrix}1 \\ x \\ x^2 \\ x^3\end{pmatrix}=\begin{pmatrix}x \\ 2x^2 \\ 3x^3 \\ 0\end{pmatrix}$

となりますが，おかしくはないでしょうか．右辺を微分しても左辺にはならず，左辺を微分しても右辺にはならないので・・・

この式はいったいどういう意味なのでしょうか．

そして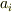， a_i がなぜないのでしょうか．

Re: 線形代数学

クロメルさんのレス (2010/01/16(Sat) 21:56)

そうですね．言葉が足りませんでしたね．例えば，

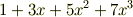
だとしたら，その係数だけを抜き出して，次のような行列を作ります．

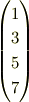
$\begin{pmatrix}1 \\3 \\5 \\7\end{pmatrix}$

という列ベクトルが対応するわけです．微分すると，

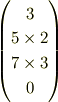
$\begin{pmatrix}3 \\5 \times 2 \\7 \times 3 \\0\end{pmatrix}$

になって欲しいので，それを満たす行列を考えると，

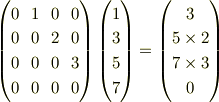
$\begin{pmatrix}0 & 1 & 0 & 0 \\0 & 0 & 2 & 0 \\0 & 0 & 0 & 3 \\0 & 0 & 0 & 0 \end{pmatrix}\begin{pmatrix}1 \\3 \\5 \\7\end{pmatrix}=\begin{pmatrix}3 \\5 \times 2 \\7 \times 3 \\0\end{pmatrix}$

となりますよね．こういうことだと思います．

Re: 線形代数学

djwk さんのレス (2010/01/16(Sat) 23:13)

ということは，今回の問題は，

$\begin{pmatrix} 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 2 & \cdots & 0 \\\vdots & & \ddots & \ddots & \vdots \\\vdots & & \ & \ddots & n \\0 & \cdots & \cdots & \cdots & 0\end{pmatrix}$

が答えでしょうか？

Re: 線形代数学

クロメルさんのレス (2010/01/17(Sun) 19:15)

返信遅れてすみません．そうです，それが答えだと思いますよ^^

[home] [掲示板] [ページの先頭]