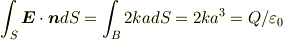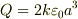電磁気
電磁気
yjddj さんの書込 (2010/01/15(Fri) 20:33)
大学１回生です．
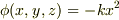で与えられる静電ポテンシャルがある．電場のx,y,z成分を求め，さらに，１辺がaで，頂点の１つが原点にあって，３辺がx,y,z座標の正方向に伸びている立方体がある．この立方体内部に含まれている全電荷を求めよ
という問題なのですが，
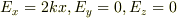で，全電荷を求めるには，積分形のガウスの法則
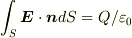を用いるような気がするのですが，どうすればよいかわかりません．
どうすればよいのでしょうか．
Re: 電磁気
mNeji さんのレス (2010/01/15(Fri) 21:06)
お書きになっているように，「積分形のガウスの法則」を実行すれば良いとおもいます．
電場がx軸方向にしかないので，立方体の表面のうちで「yz面を持ち，かつ，(x=-a/2)と(x=+a/2)の面」での積分だけを考えれば十分ではないでしょうか．
Re: 電磁気
mNeji さんのレス (2010/01/15(Fri) 21:50)
他の面の法線は，電場と垂直になります．
Re: 電磁気
yjddj さんのレス (2010/01/15(Fri) 22:00)
他の面というのは，x=aや，x=a/3といったものも含んでいるのでしょうか．
これらの面の法線も電場と平行になると思うのですが・・・
Re: 電磁気
mNeji さんのレス (2010/01/15(Fri) 23:31)
あ，立方体の中心が原点かと勘違いしていました．
＞１辺がaで，頂点の１つが原点にあって，３辺がx,y,z座標の正方向に伸びている立方体がある．
という意味では，「x=0でのyz面(0<=y<=a,0<=z<=a)」と「x=aでのyz面(0<=y<=a,0<=z<=a)」で良いですね．
なお，この場合の面積分は立方体表面で，内部から外部に向かった法線(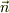 
)と，その表面での電場( 
)との内積の積分ですよね．
Re: 電磁気
yjddj さんのレス (2010/01/16(Sat) 01:01)
「x=0でのyz面(0<=y<=a,0<=z<=a)」と「x=aでのyz面(0<=y<=a,0<=z<=a)」 だけでよいのでしょうか？立方体内部ということは，0<=x<=aのyz面を考えなければならないのではないでしょうか？
そして・・・肝心のEを求める式が分かりません・・・
Re: 電磁気
mNeji さんのレス (2010/01/16(Sat) 01:50)
＞立方体内部ということは，0<=x<=aのyz面を考えなければならない
これは誤解です．もともと，微分形式のガウスの法則は；
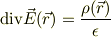
と記述されます．
これを，考える領域について体積分しますと，その結果右辺はその領域内にある電荷を意味します．他方，左辺は，「ガウスの発散定理」により，その領域の表面積分になります，それが「No.26140でお書きになった積分形式のガウスの法則」で，あくまで「考える領域の表面」に付いての面積分です．
もう一度，電磁気かヴェクタ解析の本をお読みになることをお勧めします．
また ＞肝心のEを求める式
ですが，
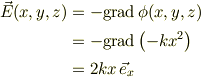
で，これも，すでにご自分で算出されているのでは？
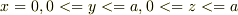のyz面での電場は０
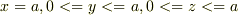のyz面(Bとする)での電場は2ka
