微分方程式
微分方程式
tip さんの書込 (2010/01/15(Fri) 03:08)
LCR直列回路に電圧Eの直流電源を印加した場合の流れる電流を微分方程式 で解くという問題なのですが,Rが定数の場合は解くことができたのですが Rが電流に依存する抵抗という仮定で微分方程式を解くことができません.
立式は初期条件がコンデンサに電荷が蓄えられておらず,電流が0という条件ならば, t=0のときi=0,i'=E/L Li''+(R(i)*i)'+i/C=0 となると考えました.
(R(i)*i)'の部分をどのように考えればいいのかよく分かりません. とりあえず分解して R(i)*i'+i*(R(i))' としましたが,ここからよく分からなくなりました.
以上よろしくお願いします.
Re: 微分方程式
mNeji さんのレス (2010/01/15(Fri) 14:03)
私も良く判りませんが,
>Li''+(R(i)*i)'+i/C=0 >となると考えました.
この式は,もともと
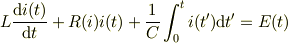
の辺々を時間で微分して得られる式ですよね.ですから,「(R(i)*i)'の部分」は そのまま,
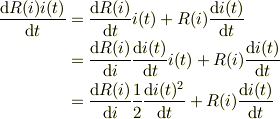
とするのでは無いでしょうか.
当然ですが, 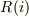 の関数形は問題で与えられているのでしょうか.お判りでしょうが,非線形な微分方程式になってしまいますね.
の関数形は問題で与えられているのでしょうか.お判りでしょうが,非線形な微分方程式になってしまいますね.
Re: 微分方程式
tip さんのレス (2010/01/16(Sat) 01:52)
回答ありがとうございます.
非線形微分方程式は今まで解いたことがないので,調べてみました.
非線形微分方程式は解析的にとくことができないため,線形化して解くか 連立微分方程式にして数値計算法で求める
ということになるのでしょうか?
因みに R(i)は2通りあってA/iとA{exp(B*i)-1}です.
前者はLi''+i/C=0 と線形化できますが,t=0でi=0とすると抵抗が無限大になるので電流が 流れなくなるため,微量電流i0が流れているという仮定で解くということ だと思います. そのため初期値がt=0のときi=i0でi'=(E-A)/Lとなると思います.
後者については数値計算法しか無理かなと思っています.
Re: 微分方程式
mNeji さんのレス (2010/01/16(Sat) 02:01)
>非線形微分方程式は解析的にとくことができないため,線形化して解くか >連立微分方程式にして数値計算法で求める
という事だと思います...,一般的には.
逆に言えば,R(i)がどのような関数であるかによって状況が変化しそうですね.