曲面積
曲面積
djwk さんの書込 (2010/01/12(Tue) 21:57)
現在,大学1回生です.
解析学の曲面積の問題です.
円柱 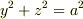 の
球
の
球 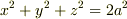 の内部にある部分の曲面積を求めよ.(a>0)
の内部にある部分の曲面積を求めよ.(a>0)
という問題で,
曲面積の公式
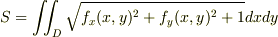 を使うのはわかるのですが,どうすればよいかよく分かりません.
を使うのはわかるのですが,どうすればよいかよく分かりません.
どうすればよいのでしょうか.
ちなみに,答えは, 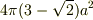 です.
です.
Re: 曲面積
Yokkun さんのレス (2010/01/12(Tue) 23:13)
> 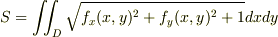
うーむ.そんなおおげさな・・・という気もします.
高さ 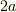 ,半径
,半径  の円柱側面と,中心角
の円柱側面と,中心角 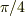 の円錐面で切り取られる半径
の円錐面で切り取られる半径 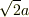 の球面が2つ分ですから,
の球面が2つ分ですから,
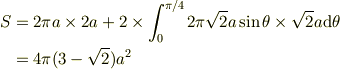
でどうでしょうか?
公式の応用練習という限定つきならば,下記が参考になると思います.
Re: 曲面積
djwk さんのレス (2010/01/15(Fri) 18:41)
お返事遅れてすみません. 回答ありがとうございます.
質問があるのですが,
中心角 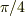 の円錐面で切り取られる半径
の円錐面で切り取られる半径 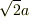 の球面が2つ分
の球面が2つ分
というのはどういう意味でしょうか.
積分部分の意味もよくわかりません・・・
Re: 曲面積
Yokkun さんのレス (2010/01/15(Fri) 21:22)
>円柱 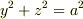 >の
>球
>の
>球 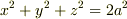 >の内部にある部分
>の内部にある部分
は,2つの部分に分けられますね?
- 高さ
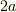 ,半径
,半径  の円柱側面
の円柱側面 - 中心角
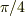 の円錐面で切り取られる半径
の円錐面で切り取られる半径 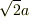 の球面が2つ分
の球面が2つ分
(2)はつまり,円柱によって切り取られた球面部分の面積です.下図の赤い部分になります.
Re: 曲面積
djwk さんのレス (2010/01/15(Fri) 21:34)
円錐面というのは,どの部分のことをいっているのでしょうか.
中心角 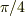 とはどこの角度か,円錐の底面の円はどの部分か,がわかりません・・・
とはどこの角度か,円錐の底面の円はどの部分か,がわかりません・・・
Re: 曲面積
Yokkun さんのレス (2010/01/15(Fri) 21:44)
わかりにくくてごめんなさい.
積分の際に中心角を用いるために,「円柱で切り取られた球面」を,「円錐で切り取られた」としたわけです.
Re: 曲面積
djwk さんのレス (2010/01/15(Fri) 22:18)
すみません.図を載せていただいていたのにそれに気づいていませんでした. おかげさまで,どの部分かはわかりました.しかし,積分の意味がわかりません・・・
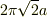 というのは,球の中心を通る,半径
というのは,球の中心を通る,半径 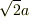 の円の円周の長さで,それに
の円の円周の長さで,それに 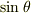 をかけたものとは一体なんなのでしょうか.最後に球の半径を掛けていますが,どういう意味でしょうか.また,中心角は,
をかけたものとは一体なんなのでしょうか.最後に球の半径を掛けていますが,どういう意味でしょうか.また,中心角は, 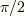 だと思うのですが,間違っているでしょうか.
だと思うのですが,間違っているでしょうか.
Re: 曲面積
Yokkun さんのレス (2010/01/16(Sat) 09:02)
円柱の軸からの中心角が  にある微小角
にある微小角 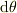 によって切り取られる球面のリング状の帯の面積を考えます.その幅は
によって切り取られる球面のリング状の帯の面積を考えます.その幅は 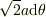 で,半径が
で,半径が 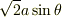 ですから,面積は
ですから,面積は
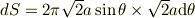
になります.これを, 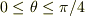 にわたって積分すれば,丸いふたの部分の面積が得られます.
にわたって積分すれば,丸いふたの部分の面積が得られます.
先ほどのURLにもうひとつアップした図を参考にしてください.