流れ関数の算出方法

流れ関数の算出方法

Flow さんの書込 (2010/01/12(Tue) 15:25)

はじめて投稿させていただきます．

2次元流れの渦を計測しているのですが， 今，各点における流速（u,v）が分かっているとします． それを合成して滑らかにつなぐと流線（流れ関数Ψ=const.）になると思うのですが， 速度から流れ関数を算出したい場合，どのように変換すればいいかが分からずに困っています． 渦度と流れ関数の関係の2次元ポアソン方程式ξ=-∇^2(Ψ)を用いれば良いのかとも考えていますが，数学が苦手なもので，どのように計算すればよいか…．

みなさんの知恵をお貸しいただければと思い，投稿させていただきました． よろしくお願いします．

Re: 流れ関数の算出方法

Yokkun さんのレス (2010/01/12(Tue) 19:51)

あまり詳しくはないのですが，と言い訳をしておいて・・・と．

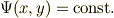
\Psi(x,y) = {\rm const.}

を，

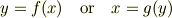
y = f(x) \quad {\rm or} \quad x = g(y)

と書き換える事ができるとして，

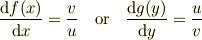
\frac{{\rm d}f(x)}{{\rm d}x} = \frac{v}{u} \quad {\rm or} \quad \frac{{\rm d}g(y)}{{\rm d}y} = \frac{u}{v}

となると思います．ただし，関数が一価連続関数になるように必要に応じて場合分けします．これを微分方程式として解けばいいのではないでしょうか．もし，この方法で関数形が得られれば，これを流れ関数に変形するのは難しくないと思います．

Re: 流れ関数の算出方法

toorisugari no Hiro さんのレス (2010/01/13(Wed) 20:18)

一本の流線を引くだけならYokkunさんのおっしゃるように微分方程式を立てて，それを積分すればいいです．でも，流れ関数をもとめるには向かないでしょうね．

結局，2次元ポアソン方程式

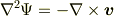
\nabla^2 \Psi &= -\nabla\times\bm{v}

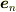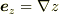に，境界条件( \bm{e}_n は境界内向き単位法線ベクトル， \bm{e}_z=\nabla z )

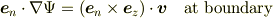
\bm{e}_n\cdot\nabla \Psi &= (\bm{e}_n\times\bm{e}_z) \cdot \bm{v} \quad\text{at boundary}

を与えて，解くしかないですね．

Re: 流れ関数の算出方法

Yokkun さんのレス (2010/01/13(Wed) 20:47)

>一本の流線を引くだけなら・・・

なるほど．よくパソコンで使う手なので，それを思い出して１本１本の流線を引くことしか頭にありませんでした．＾＾；

Re: 流れ関数の算出方法

Flow さんのレス (2010/01/13(Wed) 21:47)

Yokkunさんtoorisugari no Hiroさん 回答ありがとうございます． おっしゃるとおりポアソン方程式に境界条件を与えて解くのが良いみたいですが，

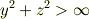
y^{2}+z^{2} &> \infty

の境界条件で解くと，

\psi &= -1/{4\pi}\iint \xi(y0,z0)\ln[(y-y0)^{2}+(z-z0)^{2}]dy0dz0

となるらしいのですが，その変形過程(なぜそうなるのか)が分かりません． また，その積分(dy0,dz0での積分)の仕方も自信がありません．

質問ばかりで申し訳ありませんが，ご教授願います．

Re: 流れ関数の算出方法

toorisugari no Hiro さんのレス (2010/01/14(Thu) 11:56)

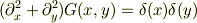
(\partial_x^2+\partial_y^2)G(x,y) = \delta(x)\delta(y)

の解が

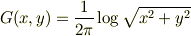
G(x,y) = \frac{1}{2\pi}\log\sqrt{x^2+y^2}

であることは，方程式を極座標系に座標変換して積分すれば導かれるはず． この解を使って

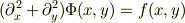
(\partial_x^2+\partial_y^2)\Phi(x,y) = f(x,y)

の一般解を

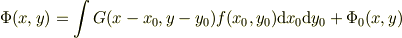
\Phi(x,y) = \int G(x-x_0,y-y_0)f(x_0,y_0)\mathrm{d}x_0\mathrm{d}y_0+ \Phi_0(x,y)

と表せます．ただし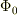， \Phi_0 は任意の調和関数( 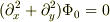(\partial_x^2+\partial_y^2)\Phi_0 =0 )です．

詳しくは２次元Poisson方程式のグリーン関数がらみで勉強してください．