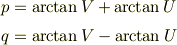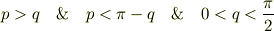簡単な幾何学だと思うのですが・・・
簡単な幾何学だと思うのですが・・・
りとるぱんだ さんの書込 (2010/01/11(Mon) 14:43)
学部生3年です.
扱う問題は一般相対論の範疇ですが,自分が問題にしたいのはたぶん高校数学の幾何学です.
一応問題の背景は書きますが,読まなくてもこの問題を考えることはできると思います.
沢山の人にこの問題を考えて頂けたら嬉しいので,相対論の知識がない方は『++++++』以降から読んで頂けたら嬉しいです.
「時空の力学 細谷暁夫著」を読んでいて,ブラックホールの中は覗くことができない,ということをペンローズ図を用いて確認する,というくだりのところで質問があります.
簡単のために,回転していない球対称なブラックホールを考えます.
計量としてシュバルツシルド時空の角度部分を無視したものを使い,まず亀座標,次にクルスカル座標に変数を変換します.
その後,ブラックホールの中も外も,このクルスカル座標で表現するためにこの座標を拡張します.
次にすべての時空をコンパクトに表現するためにペンローズ図を使って考えます.
このペンローズ図の書き方について質問させて下さい.
一応すべての座標変換について記します.
極座標で考えるので,  はブラックホールからの距離で,
はブラックホールからの距離で, 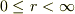 です.
全ての時空を扱うので時間は
です.
全ての時空を扱うので時間は 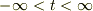 をとり得るとします.
をとり得るとします.
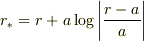 (亀座標)
とおくと,とり得る値は
(亀座標)
とおくと,とり得る値は 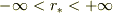 です.
です.
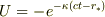
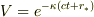 (
(  は正の定数,また
は正の定数,また 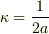 )
とおくと,
++++++++++++++++++++++++
)
とおくと,
++++++++++++++++++++++++
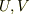 は独立に
は独立に 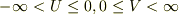 の値をとり得ます.
ここで
の値をとり得ます.
ここで
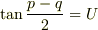
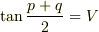 とすると,
とすると,
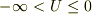
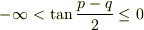
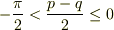
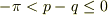 ・・・?
同様に,Vから
・・・?
同様に,Vから
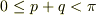 ・・・?
が得られるので,?,?の4つの条件式から,許されるp,qの範囲を
pq平面に描くと,ひし形のようになることがわかると思います.
・・・?
が得られるので,?,?の4つの条件式から,許されるp,qの範囲を
pq平面に描くと,ひし形のようになることがわかると思います.
問題はここからです.
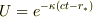 ・・・?
・・・?
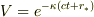 ・・・?(
・・・?(  は正の定数)
とし,とり得る値が
は正の定数)
とし,とり得る値が 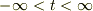 ,
, 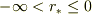 だとすると,
だとすると, 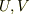 は独立に
は独立に 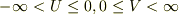 の値をとり得ることはできません.
このとき上と同様に
の値をとり得ることはできません.
このとき上と同様に
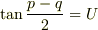 ・・・?
・・・?
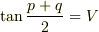 ・・・?
とすると,許されるp,qの範囲をpq平面に描くと,どのようになるでしょうか?
これを導く考え方がわかりません.よろしくお願いします.
・・・?
とすると,許されるp,qの範囲をpq平面に描くと,どのようになるでしょうか?
これを導く考え方がわかりません.よろしくお願いします.
?,?からtもしくはrを消去し,その式に?,?を代入すると,p,qの陰関数が出てきます. ここから許されるp,qの範囲がわかりそうなのですが,思うようにいきません.
ちなみに許されるp,qの範囲は
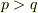 かつ
かつ 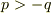 かつ
かつ 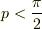 になるようです.(ひょっとしたら不等号はイコールが入るかもしれません・・・)
になるようです.(ひょっとしたら不等号はイコールが入るかもしれません・・・)
また詳しい背景が(ちょうど自分が読んでいる本のこのくだりを解説している)↓のページにあるので興味があるかたは読んでみて下さい.
- http://teenaka.at.webry.info/200701/article_13.html
- http://teenaka.at.webry.info/200701/article_14.html
- http://teenaka.at.webry.info/200701/article_15.html
よろしくお願いします.
Re: 簡単な幾何学だと思うのですが・・・
りとるぱんだ さんのレス (2010/01/12(Tue) 14:16)
Yokkunさん返信ありがとうございます. tanの逆関数使うときれいになりますね! その方法で解決しました. ありがとうございました.