一般相対論 共変微分の交換関係
一般相対論 共変微分の交換関係
りとるぱんだ さんの書込 (2010/01/07(Thu) 22:03)
学部生3年です.
一般相対論に苦戦しています.
参考書として「一般相対性理論 内山龍雄著」を読んでいて,共変微分の交換関係からリーマンテンソル 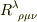 を定義する,というくだりのところで困っています.
「その参考書があなたのレベルに合っていない」と言われたらその通りです.すいません.
を定義する,というくだりのところで困っています.
「その参考書があなたのレベルに合っていない」と言われたらその通りです.すいません.
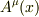 を任意の反変ベクトル場として,これを2回,共変微分します.ナブラは共変微分を表します.
を任意の反変ベクトル場として,これを2回,共変微分します.ナブラは共変微分を表します.
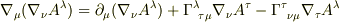
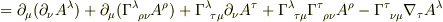
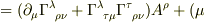 ,
,  について対称な項
について対称な項 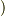 この3行が参考書には書いてあるのですが,問題は2行目の式です.
2行目の第1項,第5項はもちろん
この3行が参考書には書いてあるのですが,問題は2行目の式です.
2行目の第1項,第5項はもちろん 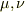 の交換に対して不変だということがわかるのですが,第3項が
の交換に対して不変だということがわかるのですが,第3項が 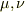 の交換に対して不変だということが理解できません.
この第3項が
の交換に対して不変だということが理解できません.
この第3項が 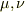 について対称となっていることをどなたか証明お願いします.
よろしくお願いします.
について対称となっていることをどなたか証明お願いします.
よろしくお願いします.
Re: 一般相対論 共変微分の交換関係
旅行者 さんのレス (2010/01/07(Thu) 22:38)
添え字が多くて大変ですね.
本当は実際に計算するべきなのですが,大変そうなので気付いた部分だけ指摘させてください.すみません.
2行目の2項目ですが, 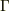 は場所の関数なので,これも微分の対象になります.ですから,2項目は
は場所の関数なので,これも微分の対象になります.ですから,2項目は
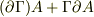 と二つの項が出てきます.これと3項目とがセットで対称になるということではないのでしょうか?
と二つの項が出てきます.これと3項目とがセットで対称になるということではないのでしょうか?
Re: 一般相対論 共変微分の交換関係
yama さんのレス (2010/01/07(Thu) 23:01)
旅行者さんが指摘されている通りだと思います.
具体的には
第2項+第3項 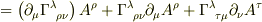 となり,右辺の第2項と第3項をひとまとめにして考えると,これは
となり,右辺の第2項と第3項をひとまとめにして考えると,これは 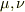 の交換に対して不変ですね.
の交換に対して不変ですね.