微分形式の内積

旅行者さんの書込 (2010/01/06(Wed) 01:53)

4次元時空での体積要素(リウビルの定理)の話です．特殊相対論で考えて頂いて構いません． pを四元運動量とし，1形式 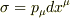$\sigma =p_{\mu}dx^{\mu}$ に対して3次元体積形式を 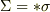$\Sigma =*\sigma$ と定義し，また 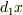$d_{1}x$ を微小ベクトルとして 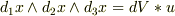$d_{1}x\wedge d_{2}x\wedge d_{3}x=dV*u$ と体積dVを定義すると(uは単位ベクトル) $\Sigma[d_{1}x\wedge d_{2}x\wedge d_{3}x]=(*\sigma \cdot *u)dV=-p_{\mu}u^{\mu}dV$ となるらしいのですが，この式がどういう計算なのか分かりません． Σは3形式なので，値を得るには $\Sigma[d_{1}x\wedge d_{2}x\wedge d_{3}x]$ ではなく $\Sigma[d_{1}x,d_{2}x,d_{3}x]$ ではないのかと思いました．また，3形式Σと3ベクトルdV(*u)の次元は同じなので，内積の一種かとも思ったのですが最後にマイナスがついてる所が腑に落ちません．

Re: 微分形式の内積

Katsuharu さんのレス (2010/01/06(Wed) 15:20)

前後の文脈が良くわからないので，なんとも答えようがないと思います．

Λそのものは，計算機科学における「Λ計算」のような気もします．しかしながら，通常そのような論文？または教科書での記法では基本的に用いません．

できれば出典を提示していただきたく．

Re: 微分形式の内積

Yokkun さんのレス (2010/01/07(Thu) 20:16)

私も微分形式を教えられる力は全くないのですが．

$\Sigma[d_{1}x\wedge d_{2}x\wedge d_{3}x]$

3形式どうしの内積になっているように思います．「最後にマイナス」は，ミンコフスキーの計量からくるマイナスではないのでしょうか？

的外れでしたら，ごめんなさい．

Re: 微分形式の内積

旅行者さんのレス (2010/01/07(Thu) 22:17)

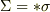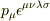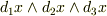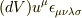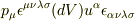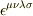お二人とも返信ありがとうございます．＞Yokkunさん私も微分形式は物理の本でしか勉強したことがないのですが，形式の内積というのは見つけられませんでした．(形式とベクトルの縮約なら見つけましたが．) 一応，単純に内積を計算してみると， $\Sigma =*\sigma$ の成分は $p_{\mu}\epsilon^{\mu\nu\lambda\sigma}$ ， $d_{1}x\wedge d_{2}x\wedge d_{3}x$ の成分は $(dV)u^{\mu}\epsilon_{\mu\nu\lambda\sigma}$ なので，内積は $p_{\mu}\epsilon^{\mu\nu\lambda\sigma}(dV)u^{\alpha}\epsilon_{\alpha\nu\lambda\sigma}$ となると思います．この成分の $\epsilon^{\mu\nu\lambda\sigma}$ を下添え字のレビチビタテンソルに直すとき，必ずどこか一箇所に0があるので，そこからマイナスが一つ出てきそうです．ただ，やはり形式の内積を取ることの物理的解釈が分からないです．形式から値を得るには，内積をとるのではなく，形式の次数個のベクトルを変数にとらせるのが普通だと思うのですが．

Re: 微分形式の内積

Yokkun さんのレス (2010/01/08(Fri) 11:55)

下記にあるような，3-ベクトルの内積のように見えたのですが，自信はありません．

http://www12.plala.or.jp/ksp/differentialforms/pVectorSpace/

もしそうであるならば，

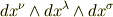
$dx^\nu\wedge dx^\lambda\wedge dx^\sigma$

と

$dV*u=d_1x\wedge d_2x\wedge d_3x$

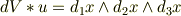
との内積は，一種の座標変換のように考えると基底どうしの内積すなわちヤコビアンになるように見えるのですが，勘違いでしょうか？ちなみに，

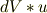
は，イメージとしては体積素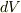に対する法線ベクトルみたいなものですよね？

Re: 微分形式の内積

旅行者さんのレス (2010/01/08(Fri) 18:24)

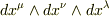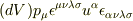ご紹介いただいたページ拝見しました．行列式で書かれていたので面食らいましたが，ようは $dx^{\mu}\wedge dx^{\nu}\wedge dx^{\lambda}$ の添え字を0〜3から3つ選んだとき，同じ数字の組を選んだ基底同士の内積だけ残る，という理解で合っていますでしょうか？それならば，成分は $(dV)p_{\mu}\epsilon^{\mu\nu\lambda\sigma}u^{\alpha}\epsilon_{\alpha\nu\lambda\sigma}$ で良さそうです．重複分の係数をどこかで付け忘れてしまいましたが，それを別にすれば 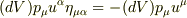$(dV)p_{\mu}u^{\alpha}\eta_{\mu\alpha}=-(dV)p_{\mu}u^{\mu}$ となり答えは一致しそうです．

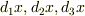物理的意味の話ですが，そもそも $\Sigma[d_{1}x\wedge d_{2}x\wedge d_{3}x]$ と $\Sigma[d_{1}x, d_{2}x, d_{3}x]$ の違いにこだわっている理由は，n形式の定義が，n個のベクトルを変数にしたとき，そのベクトルが張る体積の値を返すというもの(というふうに私は理解していますが)だからです．従って， $\Sigma[d_{1}x, d_{2}x, d_{3}x]$ ならば，その値は微小ベクトル $d_{1}x, d_{2}x, d_{3}x$ が囲む3次元体積の値という物理的意味があると思うんです．ですが，よくよく考えると $\Sigma[d_{1}x, d_{2}x, d_{3}x]$ と書いたとき変数のベクトル同士は自動的に反対称になるので結局は $\Sigma[d_{1}x\wedge d_{2}x\wedge d_{3}x]$ と同じになるような気がしてきました．(一人で勝手に話を進めていてすみません…．)

uに関しては，おっしゃるとおりです．計算を進めれば 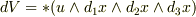$dV=*(u\wedge d_{1}x\wedge d_{2}x\wedge d_{3}x)$ が示せるので，これが体積dVの定義みたいなものだと思います．

Re: 微分形式の内積

Yokkun さんのレス (2010/01/08(Fri) 21:17)

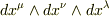> $dx^{\mu}\wedge dx^{\nu}\wedge dx^{\lambda}$ の添え字を0〜3から3つ選んだとき，同じ数字の組を選んだ基底同士の内積だけ残る，という理解で合っていますでしょうか？

私の理解はその通りですが，実は，私も今回調べてあらためて認識した内容ですので，これ以上は力に余るので控えたいと思います．

ただ，リウビルの定理＝位相空間の体積不変・・・と聞いて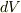，として３次元空間の体積要素をとるならば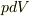， pdV は位相空間の体積積分要素で，との内積をとることでその時間変化を追跡することになるのかなあ・・・とイメージをふくらまして見たわけです．

Re: 微分形式の内積

旅行者さんのレス (2010/01/12(Tue) 18:32)

Yokkunさんの助言のおかげで答えを導くことができました．ありがとうございました．ただ，自分としては縮約の表記法がどうしても気になるので，この分野に詳しいかたがいらっしゃったらご指摘いただきたいです．

[home] [掲示板] [ページの先頭]