メスター

メスター

がくせい さんの書込 (2009/12/21(Mon) 23:11)

Ｐ．メスターの量子光学の基礎を読み始めたのですが， 最初から躓いてしまいました． 式(31),(32)がどうしても導出できません． 式(25)に(26)を代入すると 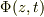\Phi(z,t) の時間微分が現れてしまいます．

これをどうやって近似するのかがわかりません．

やったことがある方，おしえていただけませんか．

Re: メスター

yt さんのレス (2009/12/23(Wed) 05:34)

がくせいさん， 取り敢えず以下のような感じで，途中までの計算をまとめてみました．

\begin{tabular}{l}|8c2c78db237d8a75b2b6c633f7a9b61a|\\\\\hspace{2em}|a7ca580541b9ed5e04f21e94e81dbe0a|\\\\\hspace{3.5em}|ac9428e8ac938de4f6b7c3508acc04d4|\\\\ \hspace{3.5em}|e5d3879a5a15723101f6e83896852435|\\\\ \hspace{2em}|11b5a113e35dcf32d9360b422871790e|\\\\\hspace{2em}|ad2ca2ffc398c406598744779b3f6581|\\\\\\|bfa5b609f7ac5c586a86a6d555d0451b|\\\\\hspace{2em}|2d230df36f9131ad4539bda5d6ee01db|\\\\\hspace{2em}|d5fdba6508c927c15a07f1e25ee21297|\\\\\hspace{2em}|7077182cbce3864cb4022bacc56597a9|\\\\\end{tabular}

前半の式では，本来はメジャーな項が相殺されてゼロとなるので１次のマイナーな項のみ残しています． 後半の式では，おそらく懸念されていた項( 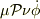\mu\mathcal{P}\nu\dot{\phi} )はメジャーな項( 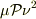\mu\mathcal{P}\nu^2 ) に比べて小さいので無視しています．(1.15式より) この種の近似計算には，高次のマイナー項が無視できる条件下の現象のみ取り扱うという意味合いと，できるだけシンプルな式から始めて何らかの基本法則を導きたいという願いが込められていると思います． そうした式で，うまくまとまらない場合は無視していた項を取り入れるなり，全く別のアプローチを探す事になります．

参考: Elements of quantum optics: Pierre Meystre,Murray Sargent [ Goolgleブックス( http://books.google.co.jp/books?id=81GSjqCIIFAC&pg=PA6# ) ]

Re: メスター

がくせい さんのレス (2009/12/23(Wed) 19:26)

長い式をわざわざ書いてくださってありがとうございます．

>>この種の近似計算には，高次のマイナー項が無視できる条件下の現象のみ取り扱うという意味合いと，できるだけシンプルな式から始めて何らかの基本法則を導きたいという願いが込められていると思います． そうした式で，うまくまとまらない場合は無視していた項を取り入れるなり，全く別のアプローチを探す事になります．

なんとなくわかりました．こういう背景を意識しながら読み進めていこうと思います． ありがとうございました．